Электрические машины

4.2. Основное уравнение коммутации

Для контура коммутируемой секции, замкнутой накоротко щеткой (рис. 4.3), можно написать уравнение

где i\ и i₂ — соответственно токи через набегающую и сбегающую коллекторные пластины, к которым присоединены концы секции;

i — ток секции; г\ и г₂ — сопротивления переходного контакта между щеткой и сбегающей и набегающей коллекторными пластинами; R_c — активное сопротивление секции. Это основное уравнение коммутации. Точного аналитического решения его не существует, так как оно является нелинейным дифференциальным уравнением с переменными коэффициентами: ЭДС е_р зависит от скорости изменения тока в самой секции и в других коммутируемых секциях, е_к зависит от распределения магнитной индукции в зоне коммутации, г, и г₂ — функции времени, а также плотности тока в щеточном контакте и скорости ее изменения, т. е. зависят от тока секции и ее производных.

Решение уравнения коммутации может быть получено при различных упрощающих предположениях. Начнем исследование с

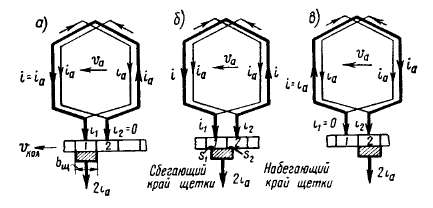
наиболее простых случаев, постепенно будем усложнять условия. Коммутация при ширине щетки, равной ширине коллекторной пластины. В этом простейшем случае коммутируется ток только в одной секции (рис. 4.4) и реактивная ЭДС учитывает только самоиндукцию и взаимоиндукцию от сторон секции, лежащей в другом слое того же паза, но замыкаемой щетками противоположной полярности.

В начале коммутации щетка соприкасается с первой коллекторной пластиной / (рис. 4.4, а), затем она перекрывает две пластины

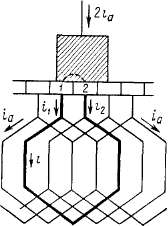
Рис. 4.3. Коммутируемая секция и токи в ней

(рис. 4.4, б); заканчивается коммутация, когда щетка соприкасается только со второй коллекторной пластиной 2 (рис. 4.4, в).

Падением напряжения в активном сопротивлении секции R_cможно пренебречь ввиду его малости, и тогда из (4.17) следует

где Lpe₃ включает взаимоиндукцию от секции другого слоя.

Разность падений напряжения под сбегающим и набегающим краями щеток в машине, работающей без искрения, очень мала и не превосходит 0,1 ...0,3 В, в то время как коммутирующая ЭДС е_к« «2,0 ...8,0 В.

Рис. 4.4 Схема распределения тока в коммутируемой секции в различные моменты времени при у=1

В связи с этим характер изменения тока в коммутируемой секции определяется ЭДС е_к и уравнение коммутации имеет вид

Ток коммутации находится интегрированием (4.19):

Постоянная интегрирования С определяется из условия равенства начального тока секции току параллельной ветви i(0)=i_o; следовательно, C=i_a и

Условие безыскровой коммутации — выход сбегающей коллекторной пластины из-под щетки без разрыва тока, для чего в момент окончания коммутации необходимо выполнение условия »₁ = 0. По-

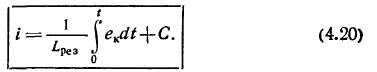
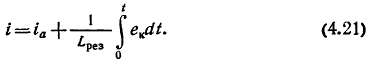
т. е. ток изменяется по линейному закону (рис. 4.5, а).

Этот закон именения тока характеризует идеальную прямолинейную коммутацию. Для нее характерно не только то, что сбегающая коллекторная пластина выходит из-под щетки без разрыва тока, но и то, что плотность тока под щеткой в местах ее соприкосновения с пластинами остается все время постоянной, равной среднему значению ]'_Щ1=jm,2=2i_a/S_m, где S_m — площадь контактной поверхности щетки. Так, например, в месте контакта щетки с первой коллекторной пластиной /im = ii/Sim, но i=i_a + i=2i_a{l—t/T_b) и площадь соприкосновения щетки с первой пластиной 5_Щ1=5_Щ(1 —

—t/T_K), т. е. ток и площадь соприкосновения убывают по одному и тому же линейному закону. Аналогично обстоит дело и с контактом щетки с набегающей пластиной 2 (см. рис. 4.4): ток £₂ и площадь контакта возрастают по одному и тому же закону.

Плотность тока мало влияет на интенсивность искрения, однако равномерное распределение тока под щеткой способствует уменьшению iiuiepb и ил^;и..^.1 контакте и поэтому считается положительным фактором.

Несоблюдение условия е_к _ср+ +е_р.ср = 0 может привести к искрению. На рис. 4.5,6 показаны графики изменения тока в коммутируемой секции, когда е_Кср меньше, чем требуется для компенсации реактивной ЭДС (кривая 2), и когда е_к ср больше требуемой (кривая 3).

В первом случае ток изменяется медленнее, чем при идеальной прямолинейной коммутации (замедленная коммутация), и в момент t—T_K, когда пластина 1 (см. рис. 4.4, в) выходит из-под щетки, происходит разрыв тока 1_0Ст> так как ток jj не равен нулю.

При ускоренной коммутации, когда коммутирующая ЭДС чрезмерно велика, выход первой пластины из-под щетки также сопровождается разрывом тока i_0CT, но направление разрываемого тока обратно по отношению к току, разрываемому при замедленной коммутации.

И при замедленной, и при ускоренной коммутации ток разрывается сбегающим краем щетки. Поэтому ГОСТ требует оценивать качество коммутации, наблюдая за сбегающим краем щетки.

Графики изменения тока на рис. 4.5,6 построены по формуле (4.25), которая выведена без учета падения напряжения в щеточном контакте. При замедленной

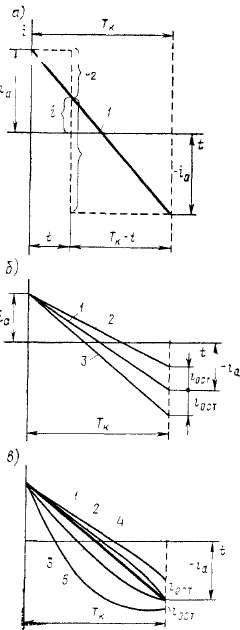
Рис. 4.5. График изменения тока в коммутируемой секции:

а — идеальная прямолинейная коммутация, б — изменение тока при е_к+е_р=5*О, в — изменение тока при е_к+е_?ф0 с учетом сопротивления щеточного контакте

или ускоренной коммутации, когда щетка разрывает ток, под сбегающим краем щетки резко возрастает плотность тока и уже нельзя пренебрегать падением напряжения, которое существенно влияет на характер изменения тока. На рис. 4.5, в показаны графики изменения тока в коммутируемой секции с учетом влияния щеточного контакта. При небольшом замедлении (кривая 2) или ускорении (кривая 3) не происходит разрыва тока. Только сильное замедление (кривая 4) или сильное ускорение (кривая 5) коммутации приводят к возникновению искрения. Более подробно о роли щеток в процессе коммутации будет сказано в § 4.3.

Коммутация сопротивлением. Исторически первой появилась и получила широкое распространение теория коммутации, в которой главная роль в процессе изменения тока отводится сопротивлению переходного контакта между щеткой и коллектором *. Она построена на аналогии между процессами на коллекторе электрической машины и механическим выпрямителем. Если бы не существовало индуктивности секции и коммутирующей ЭДС, уравнение коммутации имело бы вид

Если считать, что сопротивление щеточного контакта обратно пропорционально площади поверхности соприкосновения щетки с пластиной, то ток в коммутируемой секции изменяется так же, как при идеальной прямолинейной коммутации:

i=i_a{l-2tlT_K).

Чтобы этот закон изменения тока сохранился, когда секция имеет индуктивность, необходимо обеспечить взаимную компенсацию мгновенных значений реактивной и коммутирующей ЭДС, т. е. выполнение условия e_K+e_v = 0.

На заводах расчет проводился по среднему значению реактивной ЭДС, т. е. обе теории дали практически одинаковые рекомендации е_к.ср+е_р _Ср=0. Однако методологически уподоблять коллектор механическому выпрямителю нельзя, так как этим затушевывается характер электромагнитных процессов в машине постоянного тока. Кроме того, теория коммутации сопротивлением не могла ответить на ряд вопросов: какие проводимости учитывать при определении среднего значения реактивной ЭДС? какой выбирать форму наконечника добавочного полюса? и т. д. Разногласия вызвал вопрос о том, что делать, если сопротивление щеточного контакта нелинейно зависит от площади поверхности сопрокоснове-ния. До сих пор встречаются рекомендации импульсно менять значение коммутирующей ЭДС, чтобы пульсации ?>ДС соответствовали изменению сопротивления щеточного контакта **.

Теория среднепрямолинейной коммутации, построенная на основе анализа электромагнитных процессов, дает не только методологически ясную картину (общую для всех выпрямителей и инверторов), но и позволяет решить, как будет показано ниже, важные практические задачи при сложных условиях коммутации: щетка перекрывает несколько пластин, в пазу расположено несколько секций и т. д.

* Гипотеза предложена Э. Арнольдом и развита его последователями; наиболее законченную форму получила в трудах Р. Рихтера.

** См.: Бекишев Р. Ф. Электрические машины с коллекторами и контактными кольцами из углеродных материалов. X., 1981.

Коммутация при щенке, перекрывающей несколько коллекторных пластин; в пазу одна секция. Обычно ширина щетки Ь_щ больше коллекторного деления /_ьол и щетка перекрывает несколько коллекторных пластин:

В связи с этим коммутируется несколько секций: п или п—1, где п — ближайшее к у целое число, причем п>у.

Для коммутируемых секций можно написать систему уравнений

Таким образом, для y>1> если в слое паза расположена одна секция (и=\), требуемая коммутирующая ЭДС уменьшается соответственно увеличению щеточного перекрытия. Проводимость потоков рассеяния изменяется мало: пазовая проводимость не зависит от у, а с увеличением у увеличивается только проводимость лобовой части обмотки, где сказывается влияние взаимоиндукции соседних коммутируемых секций.

Записав одно из уравнений (4.30) в виде e_K=Lpe₃di/dt, получим закон изменения тока в секции:

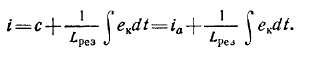
При выполнении условия е_к==е_к._Ср=const

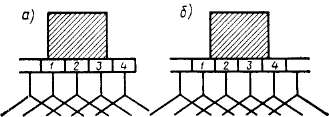
Рис. 4.6. Схема коммутации при y=2,5

т. е. аналогично случаю у=1, а условие безыскровой коммутации остается прежним: е_к._ср + е_рХр=0.

При y> 1-меняется на единицу число секций, участвующих в коммутации. Так как a"Zi_K/dttt const, скорость изменения тока в секции меняется: когда число коммутируемых секций меньше у

(рис. 4.6,а), она больше средней; когда число секций больше у (рис. 4.6,6), скорость меньше средней.

Если выбрать щеточное перекрытие равным целому числу, то, казалось бы, можно было избежать изменения числа коммутируемых

секций. Однако неизбежны технологические отступления в ширине коллекторных пластин, толщине изоляции и т. п. Это приводит к тому, что при у, равном целому числу, число коммутируемых секций изменяется от (у—1) до (-у+1), т. е. пульсирует сильнее, чем при дробном у. Поэтому рекомендуется выбирать щеточное перекрытие не равным целому числу и так, чтобы 2у приблизительно равнялось нечетному целому числу. При этом условии отклонение скорости изменения тока в коммутируемой секции от среднего получается минимальным.

Коммутация в общем случае при y>1 и ы_п>1. Обычно в слое паза лежит несколько секций, что позволяет увеличить коэффициент заполнения паза за счет уменьшения количества изоляции, снизить стоимость машины и увеличить ее мощность при заданных габаритах. Поэтому коммутация при y> 1 и ы_п>1 типична для современных электрических машин.

Число коммутируемых секций, расположенных в одноименных пазах, сначала увеличивается: коммутирует одна секция, потом две и т. д., затем уменьшается. Числу коммутируемых секций соответствуют различные результирующие индуктивности, так как непостоянен поток взаимоиндукции и соответствующая ему взаимоиндуктивность М.

Теоретические и экспериментальные исследования показали, что для секций, лежащих в одном слое паза, индуктивность L близка к взаимоиндуктивности М:

Af« (0,95... 0,99) L. (4.37)

Примем, что M»L, тогда результирующая индуктивность секции изменяется ступенями и зависит от того, сколько секций данного паза коммутирует.

Как пример рассмотрим картину коммутации при ы_п=4 и v= = 2,5. На рис. 4.7, а изображена часть обмотки якоря, на рис. 4.7, б, е — диаграммы изменения индуктивности коммутируемых секций, лежащих в одном слое паза этой обмотки.

На диаграмме рис. 4.7, б значение L«M отражено высотой прямоугольников /, 2, 3, 4, а их длина (по оси времени) равна периоду коммутации каждой секции:

Рассмотрим процесс изменения реактивной ЭДС первой секции за период коммутации.

На первом этапе, когда коммутирует только одна первая секция паза,

e_pl=-Ldi_ln/dt, (4.39)

где tin — ток первой секции. Через интервал времени

щетка замыкает накоротко вторую секцию паза и поэтому на втором этапе коммутации

e_pi = - Ldijdt - Mdijdt. (4.41)

Так как первая и вторая секции находятся в одном пазу, коммутирующая ЭДС е_к, индуцируемая в их контуре, одинакова и

dijdt xdijdt, (4.42)

и, следовательно, на втором этапе коммутации

e_r>1=-2LdiJdt. (4.43)

Аналогично для третьего этапа коммутации, когда щетка замыкает накоротко три секции данного паза,

e_pl= SLdlJdt. (4.44)

Диаграмма изменения результирующей индуктивности первой секции показана на рис. 4.7, в. На рис. 4.7, г — е показаны подобные диаграммы соответственно для второй, третьей и четвертой секций паза. Они получены суммированием высот прямоугольников (рис. 4.7, б) для одинаковых моментов времени.

Часто для всех секций паза строят общую диаграмму (рис. 4.7, ж), которая показывает, как изменяется результирующая индуктивность секций паза во время коммутации.

При нескольких секциях, лежащих в одном слое паза, не только скачкообразно изменяется результирующая индуктивность, но и увеличивается зона коммутации Ь₃._к, т. е. дуга окружности, по кото-

Рис. 4.7. Диаграмма коммутации секций одного паза при и_п = 4; Y = 2,5

рой перемещается якорь во время коммутации секций одного паза:

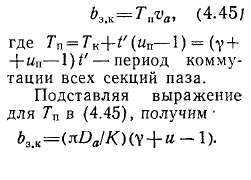
(4.46)

Для того чтобы в дифференциальные уравнения не входили переменные коэффициенты, определяемые ин-дуктивностями секций, следует рассматривать вначале не ток секции, а полный ток паза Fn~2i_aw_cUn и создаваемый им пазовый поток Ф_п = = /^гпЛп, где Л_п —проводимость потоков рассеяния, сцепленных со всеми секциями паза.

Такой прием допустим, так как секции, расположенные в одних и тех же пазах, обладают очень сильной магнитной взаимосвязью, что и позволяет рассматривать все секции паза, замкнутые щеткой (т. е. находящиеся в процессе коммутации) как один проводник, состоящий из нескольких параллельно включенных частичных проводников.

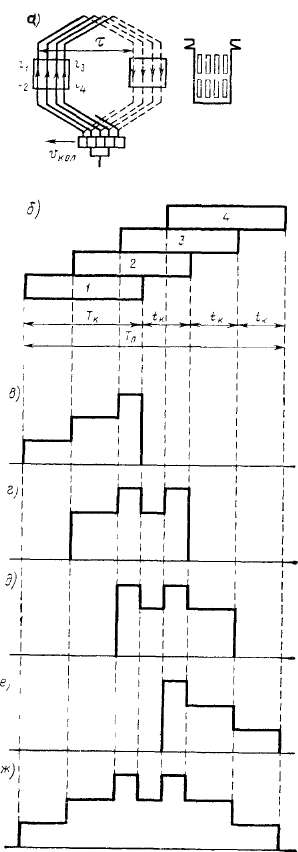
Для короткозамкнутых секций одного паза можно написать уравнение (падением напряжения в щеточ-

Одновременно с секциями рассматриваемого паза могут коммутировать и секции другого паза: в начале пазового периода коммутации— секции предшествующего паза, а в конце — секции последующего паза. Для секций другого паза аналогично:

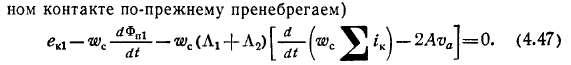
легко установить влияние ЭДС взаимоиндукции е_м на коммутацию машины: когда коммутируют секции двух пазов, ЭДС е_м замедляет коммутацию; когда коммутируют секции одного паза — ускоряет. В результате этого мгновенно я скорость изменения тока во всех коммутируемых секциях незначительно отличается от средней скорости, как уже указывалось ранее.

Среднее значение коммутирующей ЭДС е_к._ср определяется из условия, что к концу периода коммутации всех секций паза Т„ по-токосцепления паза должны быть обратными по сравнению с начальным, т. е. Дг|>п=2\|>по и

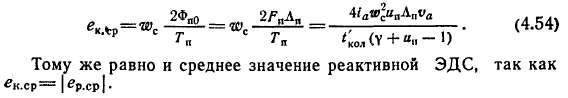
Среднее значение реактивной ЭДС определяется по формуле (4.54), а при наличии укорочения шага обмотки е_ЬОл (в коллекторных делениях)

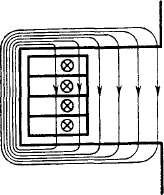
Рис. 4 8. Пазовый поток рассеяния для расположенных рядом секций

Формулы (4.25а), (4.35) и (4.546) различаются лишь коэффициентом

£ = Ип/(У + И„-1 + екат). (4-55)

который в простейшем случае, при у=\, ы_п=1. равен единице и k=l/y при ы_п=1;

Екол⁼⁼0.

В данном случае условие е_к.ср + е_рСр = = 0 относится к среднему значению реактивной ЭДС для всех секций, лежащих в одном слое паза, и, следовательно, коллекторная пластина, связанная с секцией, последней в пазу заканчивающей коммутацию, выйдет из-под щетки без разрыва тока, т. е. без искрения.

В других секциях паза, как показали опыты, изменение тока зависит не только от коммутирующей ЭДС, но и от сопротивления щеточного контакта. Когда несколько секций, расположенных рядом в пазу, замкнуты накоротко щеткой, распределение тока между ними зависит от их активного сопротивления и индуктивности рассеяния. Но так как для ряда расположенных секций пазовый поток является общим, индуктивность рассеяния очень мала (рис. 4.8) и влияние сопротивления секции и щеточного контакта велико. Сопротивление щеточного контакта меняется довольно хаотично (см. § 4.3), в связи с чем столь же хаотично меняется и ток в восьми секциях, обозначенных цифрами на рис. 4.9,6. Однако скачкообразное изменение тока в одной секции, ведет к резкому изменению тока в других короткозамкну-тых секциях, причем суммарный их ток, пропорциональный полному току паза, меняется плавно (рис. 4.9,а). Скорость изменения тока максимальна в отрезок времени Т, когда происходит коммутация секций только одного паза.

Вследствие того, что на характер изменения тока в секциях влияет сопротивление щеточного контакта, носящего в значительной сте-

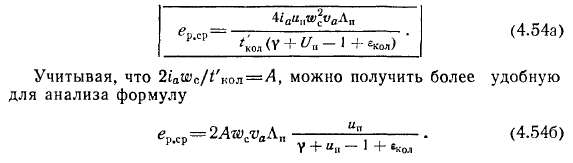
пени случайный характер, ток в секциях к концу периода коммутации может отличаться от тока параллельной ветви. Однако при резком увеличении сопротивления между щеткой и выходящей из-под нее коллекторной пластиной, связанной с секцией, заканчивающей коммутацию, ток в секции резко изменяется, что вызывает соответствующее изменение токов в остальных секциях паза, еще находящихся в стадии коммутации. Происходит демпфирование секции, заканчивающей коммутацию, другими короткозам-кнутыми секциями, лежащими рядом с ней в пазу.

Если в момент выхода пластины из-под щетки разрывается ток /₀, то в искре выделяется энергия

Рис. 4.9. Изменение тока коммутируемых секций:

а—изменение полного тока паза, б — изменение тока в секциях, расположенных в одном пазу

Так как для секций, расположенных в одних и тех же пазах, Ai = = (0,95...0,99)L, результирующая индуктивность L_pe3 очень мала, мала энергия импульса, выделяющегося под щеткой, и заметного на глаз искрения нет.

Секции, у которых ЬжМ и которые заканчивают коммутацию, когда в пазу еще есть короткозамкнутые секции, называются несамостоятельными.

При равносекционной обмотке (рис. 4.10, а), у которой секции верхнего и нижнего слоя лежат в одних и тех же пазах, все секции паза несамостоятельные, кроме одной, последней в пазу заканчивающей коммутацию. Она называется самостоятельной; практически только пластины этой секции при выходе из-под щетки могут разрывать значительный ток, т. е. создавать искрение.

Результаты этого явления хорошо известны работникам, эксплуатирующим электрические машины: на коллекторе обычно повреждаются пластины, кратные числу секций в слое паза; например, если «п=3, то подгорает каждая третья пластина; если «_п=4, то каждая четвертая и т. д.

Исключение составляют ступенчатые обмотки, в которых секции имеют разную длину, и поэтому стороны секций лежат рядом в од-

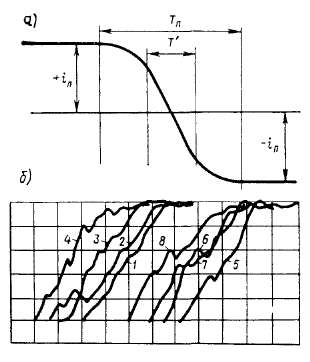
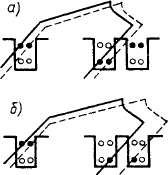
Рис. 4.10. Расположение в пазах секций ступенчатой обмотки

ном слое паза, например верхнем (рис. 4.10, б), но в другом слое они расположены в соседних пазах.

При ступенчатых обмотках в пазу может быть две или даже три самостоятельных секции, в связи с чем может подгорать большее число пластин.

Для предотвращения искрения при ступенчатых обмотках желательно, чтобы все самостоятельные секции паза заканчивали коммутацию без разрыва тока.

Содержание
Предыдущий § Следующий