3.ОСНОВНЫЕ ЗАВИСИМОСТИ И РАБОЧИЕ ХАРАКТЕРИСТИКИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
В §1 было указано, что по обмотке статора асинхронной машины протекает многофазная система токов (обычно трехфазная), которая создает в воздушном зазоре машины вращающееся магнитное поле. Вращающееся магнитное поле индуктирует (наводит) в проводниках обмотки ротора э. д, с, под действием которой в замкнутой обмотке ротора проходит ток I2, который, взаимодействуя с магнитным потоком Ф, создает механическую силу, стремящуюся привести ротор во вращение с частотой, равной частоте вращения магнитного поля статора. Частота вращения магнитного поля асинхронной машины составляет, об/мин:
п1 = 60f/p,
Частоту n1 называют также синхронной. Частота вращения ротора n зависит от режима работы машины и при работе в двигательном режиме находится в пределах 0<n<n1. Определим, с какой частотой магнитное поле машины пересекает проводники ротора. Эта частота скольжения поля относительно ротора
| n2 = n1 - n = n1 | n1 - n | = n1s |
| n1 |
Величина s, имеющая большое значение для работы асинхронных машин, называется скольжением и определяется так:
| s = | n1 - n | , |
| n1 |
| s = | n1 - n | 100, |
| n1 |
Рассмотрим работу асинхронной машины в различных режимах, которые возникают в диапазоне частот вращения ротора 0 < п < п1.
Определим частоту э. д. с. f2, которая наводится магнитным полем асинхронной машины в проводниках ротора, об/мин:
| f2 = | pn2 | , |
| 60 |
Если учесть, что n2 = n1s [см. формулу (8)], то можно записать
| f2 = | pn1 | s = fs. |
| 60 |
Здесь pn1/60 —есть частота сети. Легко видеть, что если ротор машины неподвижен, то частота э. д. с, наводимой в роторе, равна частоте сети. По мере увеличения частоты вращения ротора эта частота понижается и при синхронной частоте будет равна нулю. На рис.12 показаны изменения скольжения, частоты и э. д. с. в роторе в зависимости от частоты вращения ротора.
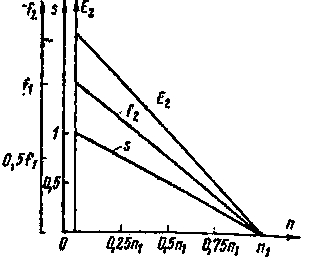 |
| Рис 12. Зависимости скольжения s, частоты f2 и э. д. с, наводимой в роторе, Е2 от частоты вращения асинхронного двигателя. |
Выражение для частоты э. д. с. в роторе дает возможность легко определить и саму э.д.с. Е2, наводимую в роторе, В:
Е2 = 4,44f2ω2k02Фмакс,
E2 = 4,44fsω2k02Фмакс = E20s,
E1 = 4,44fω1k01Фмакс ,
Напряжение U1(В), приложенное к фазе статора, должно преодолеть э. д. с, наведенную потоком, и падение напряжения в фазе. Следовательно,
U1 = - E1 + I1z1,
Величина падения напряжения I1 z1 для режимов двигателя, близких к номинальному, мала по сравнению с приложенным напряжением. Поэтому
U1 ≈ - E1.
Учитывая формулу (14), нетрудно заключить, что э. д. с. и вращающийся магнитный поток двигателя зависят от приложенного к двигателю напряжения. При постоянном напряжении поток Фмакс остается приблизительно постоянным независимо от изменения нагрузки двигателя.
Полученные соотношения составляют основу для изучения процессов в асинхронном двигателе. Рассмотрим вначале явления, происходящие в машине с заторможенным ротором и замкнутой накоротко обмоткой ротора. Асинхронный двигатель в этом режиме подобен трансформатору с короткозамкнутой вторичной обмоткой. Отличие в том, что вторичная магнитная цепь отделена от первичной воздушным зазором. Кроме того, первичная обмотка (статора) и вторичная обмотка (ротора) равномерно распределены по окружности.
Как видно из формулы (13) и рис. 12, э. д. с, наводимая в обмотке ротора, когда он неподвижен, является максимальной. В силу этого и ток, проходящий по обмоткам статора и ротора, также будет наибольшим. Ток статора в этом режиме Iк называется током короткого замыкания двигателя и превышает его номинальный ток в 4—7 раз. Двигатель в таких ненормальных условиях нельзя длительно оставлять под полным напряжением, так как сильный перегрев обмоток может привести к аварии.
Для определения параметров двигателя часто делают опыт короткого замыкания. Этот опыт заключается в том, что к заторможенному двигателю подводят пониженное напряжение, добиваясь, чтобы ток двигателя был равен номинальному току. Напряжение, подводимое к двигателю в опыте короткого замыкания, оказывается очень малым по сравнению с номинальным (обычно не более 10%). Используя этот опыт, можно в условиях, безопасных для двигателя, приближенно определить величину тока короткого замыкания Iк при нормальном напряжении, А:
| Iк = Iн | Uн | , |
| Uк |
Замеряя в этом опыте по ваттметру мощность Рк , подводимую к одной фазе двигателя, находят также cos φ в режиме короткого замыкания
| cos φк = | Pк | , |
| UкIк |
| rк = | Pк | , |
| Iн2 |
Это эквивалентное активное сопротивление равно сумме активного сопротивления статора и приведенного активного сопротивления ротора. Понятие о приведенном активном и реактивном сопротивлении ротора будет дано ниже.
Определив угол φк по величине cos φк из формулы (18), легко найти и эквивалентное реактивное сопротивление двигателя в режиме короткого замыкания, Ом:
xк = rк tg φк.
Индуктивное сопротивление xк равно сумме индуктивного сопротивления статора и приведенного индуктивного сопротивления ротора.
Поскольку частота вращения ротора двигателя в этом режиме равна нулю, его механическая мощность также равна нулю. Потери в стали во время опыта короткого замыкания очень малы, поскольку мал вращающийся магнитный поток. Поэтому мощность Рк , которая подводится к машине, почти вся идет на нагрев проводников обмотки статора и ротора. То же самое можно сказать о режиме короткого замыкания при полном напряжении.
Теперь представим себе, что обмотка ротора разомкнута, а обмотка статора включена в сеть. Ток по роторной обмотке при этом не проходит и двигатель подобен трансформатору, но уже в режиме холостого хода. Так как ток в проводниках ротора отсутствует, то механическая сила не возникает и ротор остается неподвижным.
По обмотке статора при этом проходит ток (ток холостого хода I0), который создает намагничивающую силу, необходимую для появления магнитного потока Фмакс . Поскольку в магнитной цепи асинхронного двигателя имеется воздушный зазор, то для создания магнитного потока требуется относительно больший ток, чем в трансформаторе. В двигателях большой и средней мощности ток холостого хода составляет 25—35% номинального тока, а в двигателях малой мощности 35—60%.
Наводимая в неподвижном роторе э. д. с. может быть определена по формуле (13), если учесть, что скольжение в этом режиме равно 1. Отношение э. д. с. в обмотке статора к э. д. с. в обмотке ротора называется коэффициентом трансформации э. д. с. и может быть определено по формуле
| ke = | E1 | = | ω1 k01 | ; |
| E20 | ω2 k02 |
Мощность, потребляемая двигателем в режиме холостого хода при неподвижном роторе, расходуется на потери в проводниках статора двигателя, потери на перемагничивание и вихревые токи в стали статора и в стали ротора.
Важно заметить, что режим холостого хода при неподвижном роторе очень близок к режиму, который возникает, когда двигатель не выполняет полезной работы и вращается на холостом ходу. В этом случае частота вращения ротора двигателя почти равна синхронной, а скольжение примерно равно нулю [см. формулы (8), (9) и рис. 12]. Э. д. с. в роторе будет близкой к нулю, и, следовательно, подобно режиму холостого хода при неподвижном роторе практически равен нулю ток в роторе. При холостом ходе вращающегося двигателя ток в обмотке статора, как и в случае холостого хода неподвижного двигателя, определяется в основном намагничивающей силой, необходимой для создания магнитного потока.
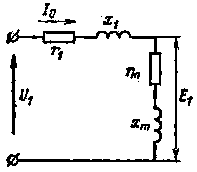 |
| Рис. 13. Схема замещения первичной цепи (статора) асинхронного двигателя, работающего в режиме холостого хода. |
При вращении ротора в двигателе появляются потери, которых нет в случае неподвижного ротора; это механические потери на трение и преодоление сопротивления воздуха. Однако когда частота вращения ротора примерно равна синхронной, исчезают потери в стали ротора двигателя, поскольку магнитное силовое поле теперь очень медленно смещается относительно ротора и его сталь почти не перемагничивается. Таким образом, потери и, следовательно, мощность в двух режимах холостого хода практически одинаковы.
Асинхронная машина в режиме холостого хода может быть представлена схемой замещения, показанной на рис. 13. Для определения характеристик машины помимо опыта короткого замыкания выполняют опыт холостого хода, во время которого замеряют ток обмотки статора I0(А) и потребляемую мощность Р0 (Вт). Это позволяет определить сопротивления в схеме замещения двигателя на холостом ходу, а также угол сдвига по фазе между током холостого хода и напряжением:
| cos φ0 = | P0 | . |
| UI0 |
Перейдем теперь к рассмотрению общего случая режима нагрузки, когда ротор вращается с частотой, меньшей частоты холостого хода. Определим, какой ток будет проходить по обмотке ротора во всем диапазоне рабочих режимов. Наводимая вращающимся магнитным потоком э. д. с. в обмотке ротора зависит при постоянном напряжении только от скольжения и может быть найдена по формуле (13). Ток ротора будет, очевидно, зависеть от э. д. с, наводимой в роторе, и сопротивления обмотки ротора. При этом полное сопротивление цепи в случае переменного тока определяется не только активным сопротивлением проводников обмотки, но и ее индуктивным сопротивлением. Индуктивное сопротивление обмотки ротора учитывает э. д. с, вызванную переменным магнитным потоком, который сцепляется только с обмоткой ротора. Эта э. д. с. ограничивает ток, протекающий в роторе, что и отражается введением индуктивного сопротивления х2δ обмотки ротора.
Наводимая потоком рассеяния э. д. с. тем больше, чем больше частота тока в роторе. Такая же зависимость справедлива для индуктивного сопротивления, Ом:
x2σ = 2πf2L2σ,
Если выразить f2 — частоту тока в роторе через частоту сети по формуле (11), то получим:
x2σ = 2πfL2σs = x2s,
Теперь, используя закон Ома для цепей переменного тока, найдем ток ротора, А:
| I2 = | E2 | . |
| √r22 + (x2σ)2 |
| I2 = | E20s | . |
| √r22 + (x2s)2 |
Таким образом, можно видеть, что при скольжении, равном нулю или близком к нему (это соответствует синхронной или близкой к синхронной частоте вращения ротора), ток ротора равен нулю или очень мал. Это совпадает с тем, что было сказано выше относительно режима холостого хода при вращающемся роторе. По мере уменьшения частоты вращения двигателя, т. е. при увеличении скольжения, ток возрастает за счет увеличения э. д. с. ротора, однако рост тока ограничивается увеличением индуктивного сопротивления ротора.
Если разделить числитель и знаменатель в выражении (26) для тока ротора I2 на s, то получим следующее выражение:
| I2 = | E20 | . |
| √(r2 /s)2 + x22 |
Из этого следует, что если мы примем, что ротор неподвижен, а его активное сопротивление меняется обратно пропорционально скольжению, то по его обмотке будет проходить точно такой же ток, как при вращающемся роторе. Такое преобразование очень удобно, потому что позволяет вместо вращающейся электрической цепи рассматривать неподвижную цепь (рис. 14).
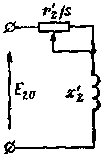 |
Рис. 14. Схема замещения вторичной цепи (ротора) асинхронного двигателя. |
Однако изучение процессов в асинхронной машине можно сделать еще более удобным, если заменить обмотку ротора, к которой приложена э. д. с. E20, обмоткой, к которой приложена э. д. с. E1. Это дает возможность в схеме замещения непосредственно электрически соединить обмотку ротора с обмоткой статора, поскольку их э. д. с. теперь одинаковы.
Замена обмотки не должна привести к изменению потребляемой мощности, потерь, намагничивающей силы и фазы тока обмотки. Из этого условия определяется новая величина тока, активного и индуктивного сопротивления обмотки ротора, которые называются приведенными величинами. Приведенный ток ротора I'2 находится по формуле
| I'2 = | m2ω2k02 | I2 = | I2 | , |
| m1ω1k01 | ki |
| ki = | m1ω1k01 | , |
| m2ω2k02 |
|
} |
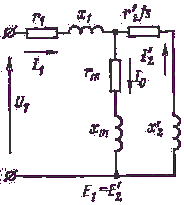
Подключая приведенную обмотку ротора к обмотке статора, получаем схему замещения асинхронной машины, показанную на рис. 15. Эту схему можно с небольшой погрешностью заменить схемой на рис. 16.
Используя последнюю схему, легко найти токи и напряжения во всех обмотках, подводимую и полезную мощность, а также мощность потерь при любой частоте вращения двигателя. Для этого следует лишь найти скольжение, соответствующее заданной частоте п по формуле (9) и вычислить сопротивление r'/s в схеме (рис. 16). После этого нетрудно найти приведенный ток роторной цепи,А:
| I'2 = | U1 | . |
| √(r1 + r'2 /s)2 + (x1 + x'2)2 |
Эта дает возможность вычислить потери в меди цепи статора, Вт:
pп1 ≈ 3[I02+ (I'2)2]r1 .
Потери в цепи ротора (Вт) можно найти, если учесть, что приведенное сопротивление ротора равно r'2:
pп2 ≈ 3(I'2)2r'2 .
Суммарная мощность, передаваемая на ротор, как видно из схемы (рис. 16), будет равна, Вт:
| Pэм = 3(I'2)2 | r'2 | . |
| s |
Эта мощность передается на ротор электромагнитным путем и называется электромагнитной мощностью.
 |
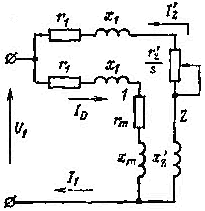 |
| Рис. 15. Т-образная схема замещения асинхронного двигателя. | Рис. 16. Упрощенная Г-образная схема замещения асинхронного двигателя. |
| Рмех = Рэм - pп2 = 3(I'2)2( | r'2 | - r'2) = 3(I'2)2r'2 | 1 - s | . |
| s | s |
Размерности величин, входящих в формулы (31) — (34):I(А); r (Ом); Р,р (Вт).
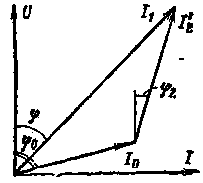 |
| Рис. 17. Диаграмма токов асинхронного двигателя. |
Полезная мощность на валу двигателя Р2 равна механической мощности Рмех за вычетом механических рмех и добавочных потерь рд . О механических потерях уже говорилось выше. Добавочные потери вызываются пульсациями потоков, проходящих в отдельные зубцы, а также несинусоидальной формой намагничивающих сил при нагрузке
Р2 = Рмех - (рмех + рд).
Определив все потери в двигателе, а также полезную механическую мощность, можно найти коэффициент полезного действия (к. п. д.) двигателя η. Коэффициент полезного действия двигателя равен отношению полезной мощности на валу двигателя ко всей мощности, подводимой к двигателю. Для его определения в каждом режиме нужно найти сумму потерь в двигателе с учетом потерь в стали рс , Вт:
Σр = рс + pп1 + pп2 + pмех + pд ,
| η = | P2 | . |
| P2 + Σр |
Используя схему замещения, можно определить также ток, потребляемый двигателем из сети, т. е. ток статора. Этот ток равен сумме двух токов. Первый из них — это ток холостого хода, который протекает по цепи 1 (см. рис. 16) и не изменяется при изменении частоты вращения ротора, второй —ток ротора I'2, который определяется по формуле (30). Складывая геометрически эти два тока, можно получить ток статорной обмотки. Такое геометрическое сложение показано на рис. 17. Угол φ2 при построении можно найти по косинусу этого угла, который вычисляется по формуле
| cosφ2 = | r + r'2 /s | . |
| √(r1 + r'2 /s)2 + (x1 + x'2 )2 |
На рис. 17 показан также угол φ2 между напряжением и током ротора. Используя все приведенные формулы, можно построить рабочие характеристики, показанные на рис. 18. Рабочими характеристиками являются зависимости частоты вращения ротора n, скольжения s, к. п. д. η и коэффициента мощности cos φ от полезной мощности, развиваемой двигателем Р2. Характеристики снимаются при постоянных значениях U1 = Uн и f = fн .
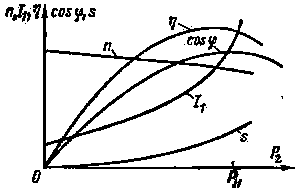 |
| Рис. 18. Рабочие характеристики асинхронного двигателя |
Рассмотрим эти характеристики. При холостом ходе, когда полезная мощность равна нулю, скольжение s также равно нулю. При этом эквивалентное активное сопротивление в цепи 2 (рис. 16) схемы замещения r'2/s равно бесконечности и ток в цепи ротора отсутствует. По цепи статора протекает только ток холостого хода I0. Коэффициент полезного действия η равен нулю, а коэффициент мощности равен коэффициенту мощности для тока холостого хода (cos φ = cos φ0 ).
При увеличении нагрузки частота вращения ротора уменьшается и увеличивается скольжение s. За счет увеличения s уменьшается сопротивление в цепи 2 и увеличивается ток ротора, а следовательно, и ток статора. Поскольку увеличивается полезная мощность, растет к. п. д. двигателя, а также коэффициент мощности. Обычно номинальная мощность на валу двигателя достигается уже при небольшом понижении частоты вращения ротора и вся область рабочих режимов находится в диапазоне скольжений от 0 до 5—10%.
Скоростная характеристика n = f(P2 ) у асинхронного двигателя имеет небольшой наклон к оси абсцисс. Характеристики такого вида принято называть жесткими. Соответственно характеристика s = f(P2 ) имеет слабый подъем при возрастании нагрузки. В асинхронном двигателе частота вращения ротора меньше частоты вращения поля, за счет чего обеспечивается наведение э. д. с и тока I2 в обмотке ротора, а также создание вращающего электромагнитного момента, под действием которого ротор приходит во вращение.
Характеристика cos φ = f(P2 ) лежит в области значений меньших 1, так как асинхронный двигатель всегда потребляет ток I0, почти не зависящий от нагрузки в диапазоне мощностей от Р0 до P2 ≈ Pн . При холостом ходе cos φ0 < 0,2. При увеличении нагрузки cos φ быстро возрастает и достигает максимального значения при мощности P2 ≈ Pн . При увеличении нагрузки свыше номинальной происходит увеличение скольжения s и cos φ несколько снижается.
Характеристика η = f(P2) лежит в области значения η<1, что обусловлено, наличием потерь в двигателе. Выше было показано соотношение между полезной мощностью Р2 и потерями Σр в асинхронном двигателе (37). Электрические потери в обмотках статора и ротора pп1, pп2 изменяются пропорционально квадрату токов (31), (32) при постоянстве температуры. Основными потерями в стали являются магнитные потери в ярме и зубцах сердечника статора от гистерезиса и вихревых токов. Величина их зависит от изменения основной гармонической составляющей магнитного потока. При увеличении нагрузки потери рс, рп, рд несколько уменьшаются. Это обусловливает изменение к. п. д. двигателя η (рис. 18).
