АСИНХРОННЫЕ
ЭЛЕКТРОДВИГАТЕЛИ

4. ВРАЩАЮЩИЕ МОМЕНТЫ И МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ

Как уже говорилось, взаимодействие тока I2 в обмотке ротора с потоком асинхронной машины Ф создает механическую силу, приводящую ротор во вращение. При определении вращающего момента, создаваемого этой силой, необходимо исходить из известного физического соотношения, согласно которому мощность, затрачиваемая на приведение тела во вращение, определяется произведением приложенного к нему момента на скорость вращения данного тела.

Как было указано в § 3, на ротор двигателя через вращающийся магнитный поток Ф передается некоторая электромагнитная мощность, рассчитываемая по формуле (33). Однако не вся мощность, переносимая на ротор магнитным потоком, расходуется на приведение его во вращение, поскольку часть ее тратится на нагревание проводников обмотки ротора.

Механическая мощность двигателя, равная разности электромагнитной  мощности  и   мощности   потерь [см. формулу (34)], будет равна произведению  вращающего момента на частоту вращения ротора:

   где М — момент, Н∙м; n — частота вращения, об/мин.

Частота вращения ротора может быть связана с частотой вращения магнитного поля машины, если вспомнить формулу (9), из которой следует:

Подставив в (39) выражение для Рмех из правой части (34) и выражение для n из правой части (40), получим:

Если теперь учесть формулу (7) для n1 и формулу (30) для I'2, то окончательно выражение для М будет иметь вид:

Во многих случаях для понимания сущности явлений, происходящих в асинхронной машине, полезно иметь в виду еще одно выражение для вращающего момента. Выше мы уже упоминали, что механическая сила, действующая на проводники ротора, создается в результате взаимодействия тока в проводниках обмотки ротора с магнитным полем. Момент асинхронного двигателя можно рассчитать, зная значение приведенного тока в роторе и потока машины

где ψ2 — угол сдвига между э. д. с. Е'2, наводимой в роторе и током ротора I'2; cм — постоянный коэффициент; Фмакс — магнитный поток, Вб; I'2 — ток ротора, А.

В области малых скольжений асинхронной машины справедливой является приближенная формула

поскольку cos ψ2 при малых скольжениях близок к единице

Используя формулу (42), можно получить достаточно полное представление о механических характеристиках асинхронного двигателя. Обратим прежде всего внимание на то, что

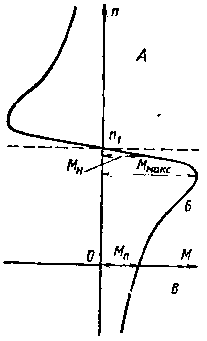Рис. 19. Естественная механическая характеристика асинхронного двигателя. А — генераторный режим; Б — режим двигателя; В — режим электромагнитного тормоза.

механический момент двигателя зависит от трех групп величин: во-первых, что величины, определяемые конструкцией двигателя, к их числу относятся r1, r'2, x1, x'2; вовторых, величины, характеризующие напряжение, подводимое к двигателю — напряжение на его зажимах U и частота питающего напряжения f; наконец, последняя величина, определяющая момент, развиваемый двигателем, зависит от режима его работы — это скольжение s.

В большинстве случаев асинхронные двигатели работают при номинальном напряжении U1, приложенном к обмотке статора и номинальной частоте питающей сети. Кроме того, параметры цепей ротора и статора двигателя, т. е. активные и индуктивные сопротивления также обычно не меняются в зависимости от режима работы. Поэтому в обычных условиях момент, развиваемый двигателем, изменяется только за счет изменения частоты вращения ротора.

Если использовать уравнение (9), то можно определить значение скольжения, соответствующее каждой заданной частоте n двигателя, и по формуле (42) вычислить величину момента для этой частоты вращения. Расчет значений момента для различных частот позволяет построить естественную механическую характеристику асинхронного двигателя, представляющую собой зависимость вращающего момента от частоты вращения ротора при номинальном напряжении на обмотках статора U1 = Uн, номинальной частоте сети и отсутствии каких-либо дополнительных сопротивлений в цепях статора и ротора. Обычно естественная механическая характеристика асинхронного двигателя имеет вид, пред ставленный на рис. 19.

Рассмотрим физические явления, обусловливающие такую форму механической характеристики. При частоте вращения ротора, равной синхронной, проводники рото­ра движутся с той же частотой, что и вращающееся магнитное поле. Поэтому э. д. с, а следовательно, и ток в роторе равен нулю. Поэтому равен нулю и вращающий момент двигателя. При уменьшении частоты вращения ротора ниже синхронной проводники обмотки ротора начинают пересекать магнитное поле машины, в результате чего в обмотке ротора наводится э. д. с, пропорциональная скольжению ротора [см. формулу (13)]. При малых скольжениях (в пределах от s = 0 до s = sк ) ток ротора также изменяется почти пропорционально скольжению. К такому выводу можно прийти, рассматривая уравнение (26) или уравнение (30). Так, в уравнении (26) при малых значениях s можно пренебречь составляющей x2s в знаменателе по сравнению со значением r2, а в уравнении (30) можно пренебречь всеми составляющими в знаменателе по сравнению со значе­нием r'2 /s.

Таким образом, ток ротора в этом диапазоне скольжений практически определяется величиной э. д. с. ротора, деленной на постоянное активное сопротивление r2 [уравнение (26)].

Если рассмотреть уравнение (43) и учесть, что поток машины Фмакс практически постоянен при изменении нагрузки двигателя, то можно прийти к заключению, что момент двигателя в области малых скольжений пропорционален току ротора. А поскольку ток ротора приблизительно пропорционален скольжению, то оказывается, что и момент в этой зоне пропорционален скольжению. Такая зависимость хорошо видна на рис. 19 при п, близких к п1.

Обычно номинальное скольжение двигателя, т. е. скольжение, при котором двигатель развивает номинальный момент, составляет малую величину порядка от 0,01 до 0,1. Поэтому зависимость момента двигателя от скольжения при изменении нагрузки от нулевой до номинальной подчиняется линейному закону.

По мере увеличения скольжения влияние индуктив­ного сопротивления обмотки ротора двигателя значи­тельно возрастает. Это приводит к тому, что зависимость между моментом и скольжением перестает быть линейной и при некотором значении скольжения s = sмакс вращающий момент достигает максимального значения Ммакс Скольжение sмакс называется критическим. Исследование условий, при которых наступает максимальный вращающий момент, показывает, что он имеет место приблизительно при таком скольжении, когда индуктивное сопротивление обмотки ротора равно ее активному сопротивлению.

Величину критического скольжения можно найти по формуле

а величина максимального момента асинхронного дви-гателя определяется по следующей приближенной формуле:

Из приведенных выражений видно, что величина максимального момента не зависит от значения активного сопротивления ротора. Активное сопротивление ротора влияет только на величину критического скольжения. Величина максимального момента, который может быть развит асинхронным двигателем, определяется в основном суммой индуктивных сопротивлений статора и ротора, поскольку значение r1 обычно весьма мало по сравнению с х1 + х'2 . Для того чтобы увеличить Ммакс, асинхронные двигатели обычно стараются проектировать с возможно меньшими индуктивными сопротивлениями рассеяния статора и ротора. Одной из важных причин, характеризующих асинхронный двигатель, является перегрузочная способность

где kм — коэффициент, определяющий перегрузочную способность; Мн — номинальный момент двигателя.

Увеличение скольжения до значений выше критического, т. е. дальнейшее понижение частоты вращения ротора, приводит к понижению величины вращающего момента.

Наконец, при скольжении, равном единице, т. е. при неподвижном роторе момент асинхронного двигателя равен пусковому моменту. Наряду с максимальным моментом он составляет одну из важных эксплуатационных характеристик двигателя. Его величина может быть получена из общей формулы момента (42), если в нее подставить s = l:

Выражение (42) может быть использовано также для расчеты вращающего момента двигателя в генераторном режиме, когда скольжения оказываются отрицательными (см. рис. 19), т. е. n>n1.

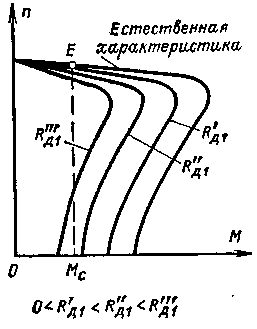Рис. 20. Механические характеристики асинхронного двигателя при различных значениях питающего напряжения (активные сопротивления-резисторы в цепи статора).

В этом режиме знак момента меняется по сравнению с двигательным режимом, поскольку меняется направление тока, проходящего через ротор.

Помимо зависимости вращающего момента асинхронного двигателя от частоты вращения ротора большое значение имеет зависимость его от напряжения, питающего двигатель. Однако такая зависимость имеет значительно более простой характер. Как видно из рассмотрения формулы (42), при заданном значении частоты вращения и скольжения ротора развиваемый двигателем момент прямо пропорционален квадрату подводимого к обмотке статора напряжения. Это значит, что при снижении напряжения на 10% момент понижается на 19%, а при снижении напряжения на 20% уменьшение момента составляет 36%. На рис. 20 изображены механические характеристики двигателя при номинальном питающем напряжении (естественная характеристика) и напряжении, пониженном за счет введения сопротивлений  (резисторов)  Rд1.

Из сказанного следует, что вращающий момент, развиваемый асинхронным двигателем, весьма чувствителен к изменению питающего напряжения. При снижении напряжения,   питающего   двигатель,   который   работает под нагрузкой, его вращающий момент снижается. В результате этого происходит понижение частоты вращения двигателя. Частота понижается (и соответственно увеличивается скольжение) до тех пор, пока вращающий момент двигателя не станет равным статическому моменту сопротивления, обусловленному

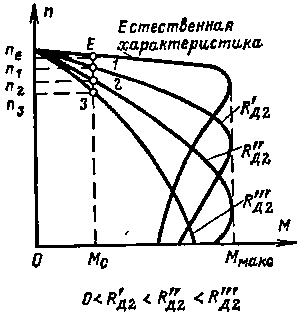Рис. 21. Механические характеристики асинхронного двигателя при различных сопротивлениях-резисторах в цепи ротора

приводом. Однако если напряжение понижается очень сильно, может случиться, что максимальный вращающий момент, который развивает двигатель при данном напряжении, оказывается меньше, чем статический момент сопротивления на его валу. В этом случае происходит опрокидывание двигателя, т. е. частота вращения ротора постепенно уменьшается и в конце концов двигатель останавливается. По его обмоткам в этом режиме проходит большой ток (см. § 3) и его необходимо обязательно отключить от сети.

Большое значение имеют механические характеристики асинхронных двигателей, получаемые при введении активного сопротивления в цепи обмоток ротора, что может быть выполнено в двигателях с фазным ротором. Механические характеристики двигателя при различных величинах дополнительных сопротивлений (резисторов) в цепи ротора Rд2 изображены на рис. 21.

При малых значениях скольжения дополнительное сопротивление в цепи ротора уменьшает ток ротора. Если учесть формулу (42), то можно увидеть, что это приводит к уменьшению момента, развиваемого двигателем при одном и том же скольжении. Из рис. 21 видно, что при заданном скольжении, т. е. при одной и той же частоте вращения n, момент тем меньше, чем больше сопротивление в цепи ротора.

Величина критического скольжения при большем сопротивлении в цепи ротора оказывается большей. Это следует из формулы (45) и физически объясняется тем, что при большом активном сопротивлении в цепи ротора индуктивное сопротивление рассеяния в роторе может стать равным ему только при большом скольжении. Наконец, величина максимального момента, развиваемого двигателем, остается одинаковой при любом сопротивлении в цепи ротора, как это следует из формулы (46).