§ 5.2. ИСПОЛНИТЕЛЬНЫЙ ДВИГАТЕЛЬ С АМПЛИТУДНЫМ УПРАВЛЕНИЕМ

Идеализированный двигатель. При амплитудном управлении напряжение управления Úy изменяется только по величине в соответствии с сигналом управления αэ , оставаясь сдвинутым по фазе на 90° относительно напряжения возбуждения Úв (см. рис. 5.1,б).

Анализ свойств асинхронного двигателя будем производить путем разложения его магнитного поля на два круговых поля — прямой и обратной последовательностей.

При равенстве чисел витков обмоток управления и возбуждения wy = wв , т. е. при симметричных обмотках двигателя, сдвинутых в пространстве на 90°, прямое и обратное магнитные поля будут создаваться соответствующими симметричными составляющими напряжений.

Представим каждый из векторов напряжений Úy и Úв в виде суммы векторов прямой и обратной последовательностей (рис. 5.5)

при этом Úу.пр = -jÚв.пp, Úу.обр = jÚв.обр.

Систему уравнений (5.4) преобразуем к такому виду

Умножим левую и правую части (5.5) на j:

Складывая (5.7) и (5.6), получаем (рис. 5.5, а) Úв.пp = 0,5 * (Úв + jÚy ).

Вычитая (5.7) из (5.6), получаем (рис. 5.5,б) Úв.обр = 0,5 * (Úв - jÚy ).
При амплитудном управлении угол между векторами  Úв и Úy равен β = 0,5π и Úy /Úв = α. Поэтому

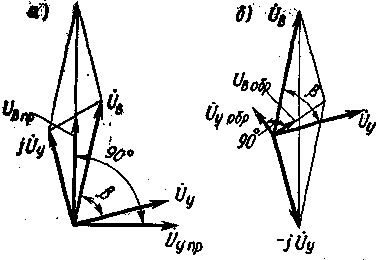Рис. 5.5. Разложение векторов напряжений, по­даваемых на двухфазную обмотку при несим­метричном ее питании на систему векторов прямой (а) и обратной (б) последовательностей

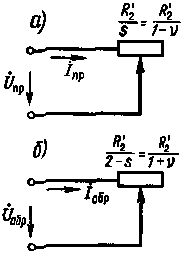Рис. 5.6. Схемы замещения идеализированного двигателя для токов прямой (а) и обратной (б) последовательностей

При α = 0 обратное поле равно прямому, т. е. результирующее поле является пульсирующим. При α = 1 обратное поле равно нулю, т.е. существует только прямое круговое поле. При 1 > α > 0 — поле эллиптическое.

Если числа витков обмоток не равны между собой, то в формулах (5.8) и (5.9) нужно вместо в подставлять эффективный коэффициент сигнала
αэ = kα = wв α/wy и сопротивления обмоток управления привести к обмотке возбуждения, т. е. принимать Rв — k2Ry ; Хв = k2Ху .

Анализ свойств исполнительного двигателя можно существенно облегчить, если расчет вести не по схеме, приведенной на рис. 4.15,а, а по упрощенным схемам замещения {рис. 5.6), в которых пренебрегают всеми сопротивлениями, кроме активного сопротивления ротора. Такие упрощенные схемы замещения называют идеализированными. Основанием для идеализации служит то обстоятельство, что ротор исполнительных двигателей делают с повышенным активным сопротивлением для устранения самохода и улучшения формы механических характеристик.

Схемы замещения для прямой (рис. 5.6, а) и обратной (рис. 5.6,б) последовательностей составляют раздельно, так как они отличаются значениями активного сопротивления ротора, которые зависят от скольжения относительно прямого и обратного магнитных полей. Для токов прямой и обратной последовательностей

где v = n2 /n1 - относительная частота вращения ротора.

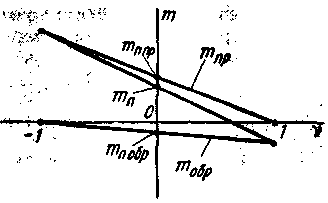Рис. 5.7. Зависимости тпр и тобр от v

В идеализированном исполнительном двигателе зависимости моментов, создаваемых напряжениями прямой и обратной последовательностей, от относительной частоты вращения v — линейные (рис, 5.7). Поэтому их можно строить по двум точкам. Для момента прямой последовательности удобно в качестве одной взять точку при v = 1 (режим холостого хода), при которой момент равен нулю (скольжение равно нулю), а вторую точку при v = 0 (режим пуска), когда ток двигателя определяется только сопротивлением ротора

При v = 0 электромагнитная мощность, создаваемая токами прямой последовательности (для обеих фаз статора)

а пусковой момент

Выразим момент в относительных единицах, приняв за базовую величину значение момента при v = 0 и αэ = l, т. е. при круговом поле

При этом в относительных единицах получим

Для момента обратной последовательности одну из точек целесообразно взять при v = 0, а другую при v = - 1. Для точки, соответствующей v = 0, на основании тех же преобразований получим значение пускового момента, создаваемого токами обратной последовательности в относительных единицах:

При v = - 1 момент обратной последовательности равен нулю. Соединив прямой две точки, получим в относительных единицах результирующий момент:

при v = - 1

при v = 1

Принимая зависимость m = f(v) в виде m = а - bv, определяем коэффициенты а и b из условий:

при v = 0

при v = 1 т = a - b = 2тп.обр , откуда

Следовательно, искомая зависимость имеет вид

По формуле (5.17) можно построить механические характеристики исполнительного двигателя в относительных единицах: m = f(v) (рис. 5.8,а), т.е. общие для всех двигателей при амплитудном управлении (при идеализированных условиях) независимо от их индивидуальных свойств, абсолютного значения момента, частоты вращения и т. п. При неизменном коэффициенте сигнала зависимость m = f(v) является линейной. Относительный момент при трогании численно равен эффективному коэффициенту сигнала αэ . С изменением αэ изменяется и наклон механической характеристики, что является недостатком рассматриваемого способа регулирования.

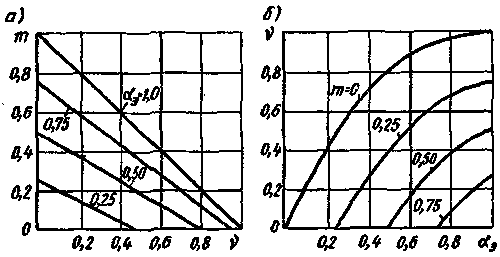Рис.   5.8.   Механические   и   регулировочные   характеристики идеализированного двигателя с амплитудным управлением

Частоту вращения при холостом ходе v0 можно получить из условия m = 0, т. е.

откуда

Снижение частоты вращения в режиме холостого хода при меньших значениях αэ объясняется тормозящим действием обратного поля. Регулировочные характеристики (рис. 5.8,б) показывают, как изменяется частота вращения исполнительного двигателя при изменении коэффициента сигнала, если момент (нагрузка) на валу двигателя остается постоянным. Уравнение регулировочной характеристики получим, решая (6.17) относительно v:

Начальные точки кривых v = f(αэ ) (рис. 5.8,б), лежащие на оси абсцисс, характеризуют чувствительность двигателя. Минимальное напряжение, при котором ротор начинает вращаться, преодолевая заданный тормозной момент, называют напряжением трогания. Из рисунка видно, что даже в идеализированном двигателе регулировочные характеристики являются нелинейными, что вызывает существенные затруднения при проектировании автоматического устройства и требуют применения ряда дополнительных элементов.

Реальный двигатель. Характеристики реального двигателя должны определяться по полной схеме замещения, позволяющей учитывать влияния намагничивающего тока, падения напряжения в обмотках статора и индуктивном сопротивлении ротора. Не касаясь конкретных особенностей машины, рассмотрим основные отличия характеристик реального исполнительного двигателя от характеристик идеализированного.

Механические характеристики m = f(v) для реального двигателя с амплитудным управлением изображены сплошными линиями на рис. 5.9, а; там же штриховыми линиями показаны характеристики идеализированного двигателя. Сравнивая указанные характеристики, можно отметить следующее:

а) в реальном двигателе при холостом ходе и αэ < 1 относительная частота вращения больше, чем в идеализированном. Это объясняется тем, что с повышением относительной частоты вращения ротора v влияние его индуктивного сопротивления Х2 на ток прямой последовательности уменьшается, а на ток обратной последовательности увеличивается, так как R2 /(1 - v) > R2 /(1 + v). Поэтому в реальном двигателе поток обратной последовательности меньше, чем в идеализированном. В результате уменьшается и тормозящий момент, образуемый этим потоком, что приводит к некоторому увеличению частоты вращения;

Рис. 5.9. Механические и регулировочные характеристики    реального    двигателя    с    амплитудным управлением

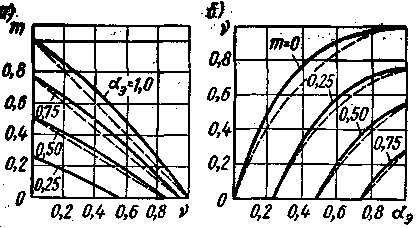б) реальные механические характеристики нелинейны, что также обусловливается в основном влиянием индуктивного сопротивления Х2 двигателя, нарушающего линейную зависимость тока ротора от относительной частоты вращения.

Регулировочные характеристики v = f(αэ ) для реального двигателя (рис. 5.9,б) проще строить по имеющимся механическим характеристикам v = f(m). Поскольку механические характеристики реального двигателя проходят выше характеристик идеализированного двигателя, то и регулировочные характеристики проходят выше характеристик идеализированного двигателя (см. штриховые линии). Иными словами, при заданном относительном моменте требуемая частота вращения в реальном двигателе достигается при меньшем значении αэ .

Для повышения точности работы автоматического устройства необходимо обеспечить линейность механических и регулировочных характеристик. Однако это требование в асинхронном исполнительном двигателе можно выполнить только приближенно. Некоторого повышения линейности механических характеристик можно достигнуть за счет увеличения активного сопротивления ротора, что, однако, ухудшает использование двигателя и уменьшает абсолютную величину вращающего момента.

Мощности управления и возбуждения у реального двигателя практически не зависят от режима его работы. Поскольку в двигателе с полым немагнитным ротором ток холостого хода достигает 85—95% от номинального, то ток возбуждения и мощность возбуждения Sв остаются примерно постоянными

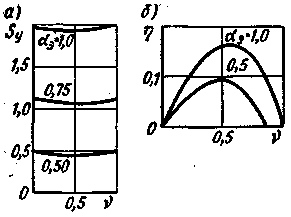Рис. 5.10. Зависимость мощности управления и КПД реального   двигателя   с   амплитудным управлением от v

при всех значениях αэ и v. Мощность управления Sy (рис. 5.10, а) также не зависит от частоты вращения v, но сильно изменяется с изменением коэффициента сигнала αэ . Это объясняется тем, что при практически неизменном сопротивлении обмотки управления мощность пропорциональна квадрату подводимого напряжения.

КПД исполнительного двигателя с полым немагнитным ротором невелик: η = 10 ÷ 20% при αэ = 1 и v ≈ 0,5v0 . Примерная зависимость его от относительной частоты вращения показана на рис. 5.10,б. Низкое значение КПД объясняется большими потерями в роторе (из-за увеличенного сопротивления) и статоре (вследствие значительного тока холостого хода). При уменьшении коэффициента сигнала КПД снижается, так как резко падает полезная мощность, а потери в статоре и роторе уменьшаются сравнительно мало. Таким образом, в асинхронных исполнительных двигателях стремление к улучшению линейности механических характеристик, повышению точности регулирования, а также к увеличению быстродействия приводит к существенному снижению КПД двигателя и ухудшению его использования, т. е. к увеличению габаритных размеров. Коэффициент мощности cos φ исполнительного двигателя с полым ротором имеет максимум при пуске: cos φmax = 0,5 ÷ 0,6. С возрастанием частоты вращения cos φ уменьшается.