§ 5.9. ЛИНЕЙНЫЙ ВРАЩАЮЩИЙСЯ ТРАНСФОРМАТОР

Выходное напряжение. При любом включении обмоток вращающегося трансформатора уравнение, связывающее его выходное напряжение с углом поворота θ ротора, содержит функции sin θ и cos θ. Однако, выбирая определенным образом схемы включения обмоток, можно получить выходную характеристику в некотором ограниченном диапазоне изменения угла θ, близкую к линейной. Например, при небольшом изменении угла θ можно считать, что θ ≈ sin θ, и получать требуемую линейную зависимость Uвых = f(θ) от синусной обмотки. Однако в этом случае желательную точность линейной аппроксимации 0,1 % можно получить только при изменении угла θ в пределах ±4,5°. Поэтому использовать для линейного поворотного трансформатора одну синусную обмотку нерационально.

Более широкий диапазон изменения угла θ, в пределах которого выходная характеристика с достаточной точностью считается линейной, можно получить, если выходное напряжение представить в виде функции

Для получения указанной зависимости применяют две схемы соединения обмоток вращающегося трансформатора: с первичным симметрированием (на статоре) и со вторичным симметрированием (на роторе).

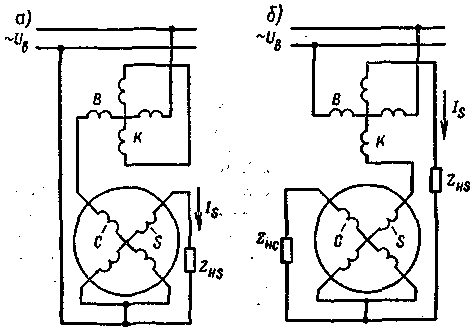Рис.   5.29.   Схемы   линейного   вращающегося   трансформатора

Первичное симметрирование. В схеме первичного симметрирования (рис. 5.29, а) компенсационную обмотку К замыкают накоротко, а обмотку возбуждения В соединяют последовательно с косинусной обмоткой С ротора; концы их подключают к сети. К синусной обмотке S присоединяют нагрузочное сопротивление ZнS. Поскольку обмотка К замкнута накоротко, поперечный поток Фq = 0. Для цепи обмоток В и С составим уравнение

Так как ЭДС, индуцированные в обмотках В и С, совпадают по фазе, то они складываются алгебраически. Поэтому с учетом (5.44) и (5.46) сумма

откуда

Следовательно, согласно (5.48) ЭДС, индуцируемая в выходной обмотке S,

Пренебрегая падениями напряжения в обмотках В, С и S и принимая Ев + ЕC ≈ Uв , получаем выходное напряжение

Если вращающийся трансформатор выполнен с k = 0,52 ÷ 0,56, то в пределах изменения угла ротора θ = ±55° выходное напряжение Uвых пропорционально этому углу.

Вторичное симметрирование. В схеме вторичного симметрирования (рис. 5.29,б) нагрузка ZнS включена в цепь последовательно соединенных обмоток S и К ; обмотка В присоединена к сети, а к обмотке С подключено симметрирующее сопротивление ZнС. Величину этого сопротивления подбирают таким образом, чтобы поперечные МДС обмоток S и С компенсировали друг друга.

При этих условиях в машине действуют постоянный по амплитуде продольный поток Фd создаваемый обмоткой В, и поперечный поток Фq, создаваемый обмоткой К и пропорциональный току нагрузки IS. Потоки Фd и Фq индуцируют в синусной обмотке ЭДС ES = kЕв sin θ + 4,44f1 w2 kоб2 Фqm cos θ, или, переходя к комплексным значениям,

где X1q — индуктивное сопротивление обмотки статора, обусловленное потоком Фq .

Так как в данном случае ÍS = ÉS/(ZS + ZнS + ZK), то уравнение (5.61) принимает вид

откуда где B́ = kjX1q /(ZS + ZнS + ZK) — некоторый комплексный коэффициент.

Если коэффициент В = 0,52 ÷ 0,56, то зависимость Uвых = f(θ) в пределах угла θ = ±55° линейная. Значение сопротивления ZнC, обеспечивающее взаимную компенсацию поперечных МДС обмоток S и С, определяется из условия

Следовательно, для вторичного симметрирования необходимо, чтобы полное сопротивление цепи косинусной обмотки равнялось удвоенному сопротивлению цепи синусной обмотки.

Преимущества и недостатки различных схем симметрирования. В линейных вращающихся трансформаторах с первичным симметрированием изменение нагрузка ZнS практически не оказывает влияния на величину ЭДС ES, т. е. на линейность выходной характеристики, так как обмотка К компенсирует поперечный поток Фq , а сопротивление ZнS ≥ ZS. Однако при изменении угла поворота ротора возникают небольшие погрешности в выходном напряжении из-за изменения тока и падения напряжения в первичном контуре.

В линейных трансформаторах со вторичным симметрированием при изменении нагрузки нарушается условие симметрирования и возникают значительные отклонения от линейной зависимости, поэтому их применяют сравнительно редко.