§ 2.5. ИДЕАЛИЗИРОВАННЫЙ ТРАНСФОРМАТОР

Для выяснения сущности физических процессов, происходящих в трансформаторе, рассмотрим идеализированный трансформатор, у которого магнитный поток Ф полностью замыкается по стальному магнитопроводу и сцеплен с обеими обмотками, а потери в стали отсутствуют. К первичной обмотке трансформатора (рис. 2.22, а) подводится синусоидальное напряжение и1 = Um sin ωt, благодаря чему по этой обмотке проходит переменный ток, создающий переменный магнитный поток. Переменный поток наводит в обмотках трансформатора ЭДС е1 = - w1 dФ/dt; e2 = — w2 dФ/dt.

В режиме холостого хода цепь вторичной обмотки разомкнута и ток i2 = 0. При этом для контура первичной обмотки трансформатора

u1 = i1r1+w1dФ/dt,                                              (2.6)

где   u1 — мгновенное   значение   приложенного   к   первичной обмотке напряжения.

Уравнение (2.6) справедливо, если принять, что не только i2 =0, но и отсутствуют потери в стали магнитопровода (от вихревых токов и гистерезиса); иначе эти потери должны были бы учитываться в виде потерь от тока, проходящего по замкнутой накоротко вторичной обмотке с большим активным; сопротивлением. Вводя в формулу (2.6) значение ЭДС e1 = - w1 dФ/dt, индуцируемой в первичной обмотке переменным магнитным потоком, и пренебрегая падением напряжения в активном сопротивлении первичной обмотки i1r1из-за его малости, получаем

u1+e1= 0,                                                     (2.7)

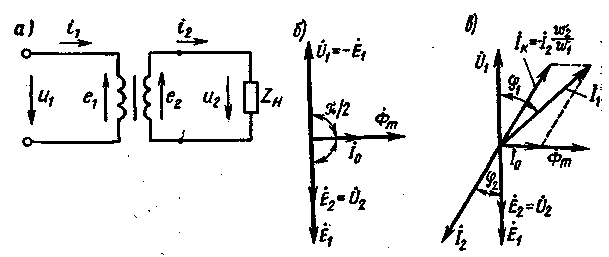Рис. 2.22. Схема включения (а) и векторные диаграммы (б, в) идеализированного трансформатора

т. е. напряжение, приложенное к первичной обмотке, практически полностью уравновешивается индуцированной в этой обмотке ЭДС.

Если питающее напряжение u1 изменяется по синусоидальному закону u1 = U1msinωt, то магнитный поток также изменяется синусоидально, отставая по фазе от приложенного напряжения на угол 90°,

Ф = ∫

u1 w1

dt =

U1m w1

∫sinωtdt = - Фmcosωt + C = Фmsin(ωt -

π 2

)

Можно показать, что постоянная интегрирования в установившемся режиме С = 0.

Связь между ЭДС и магнитным потоком определяется из уравнения

e1 = - w1

d dt

[Фmsin(ωt -

π 2

)] = -w1ωФmcos(ωt-

π 2

) = 2πfw1Фmcos(ωt - π/2)

,

и выражается  для  амплитудного значения  ЭДС формулой E1m = 2πfw1Фm

или для действующего значения формулой:

E1 = 4,44fw1Фm.

(2.8)

Учитывая синусоидальный характер изменения напряжения и1 и ЭДС е1 уравнение (2.7) можно представить в комплексной форме:

Ú + É1 = 0.

(2.9)

Уравнение (2.9) справедливо для идеализированного трансформатора, в котором пренебрежимо мало активное сопротивление обмоток и отсутствуют потери в стали магнитопровода. Однако, несмотря на принятые допущения, оно правильно определяет сущность качественных процессов, происходящих в трансформаторе, и поэтому является одним из фундаментальных в теории электрических машин. Количественные ошибки, вызванные идеализацией трансформатора, можно всегда довольно легко подсчитать.

Предположив, что насыщение в стали трансформатора отсутствует и весь магнитный поток замыкается по стальному магнитопроводу, можно считать ток первичной обмотки идеализированного трансформатора прямо пропорциональным магнитному потоку. В связи с этим на векторной диаграмме идеализированного транеформатора в режиме холостого хода (рис. 2.22,б) ток холостого хода Í0 изображен вектором, совпадающим по направлению с вектором магнитного потока Ф́т. На этой же диаграмме векторы ЭДС É1и напряжения Ú1 показаны в противофазе в соответствий с уравнением (2.9), а вектор магнитного потока Ф́m опережает вектор ЭДС на 90°. Поскольку магнитный поток не имеет действующего значения, на диаграмме показано его амплитудное значение. Там же показан вектор ЭДС Е́2, совпадающий по фазе с вектором Е́1, так как ЭДС Е2индуцируется тем же самым магнитным потоком, что и Е1и может быть определена по формуле

E2 = 4,44fw2Фm.

(2.10)

При работе под нагрузкой для первичной обмотки идеализированного трансформатора можно написать уравнение

u1 = w1

dФ1 dt

+ w1

dФ2 dt

= w1

d dt

(Ф1+Ф2),

где Ф1 и Ф2 — потоки, создаваемые токами первичной и вторичной обмоток.

Обозначая, как и при холостом ходе,

e1 = - w1

d dt

(Ф1+Ф2),

получаем

u1 +e1 = 0,

т. е. такое же соотношение, что и при холостом ходе. Очевидно, если первичное напряжение при нагрузке идеализированного трансформатора остается неизменным, то величина ЭДС et такая же, как и при холостом ходе. Следовательно, результирующий поток при нагрузке равен потоку при холостом ходе:

Ф1 + Ф2 = Ф0,

или в комплексной форме

Ф́m1 + Ф́m2 = Ф́m0.                                                      (2.11)

Неизменность магнитного потока при переходе от режима холостого хода к режиму нагрузки является важнейшим свойством трансформатора. Из этого свойства следует закон равновесия магнитодвижущих сил (МДС) в трансформаторе:

F́1 + F́2 = F́0,

(2.12)

где F1 и F2 — МДС, создаваемые первичной и вторичной обмотками трансформатора при нагрузке; F0 — МДС, создаваемая первичной обмоткой при холостом ходе.

При переменном токе оперируют с амплитудами МДС; при этом из (2.12) следует, что

√

2

Í1w1 + √

2

Í2w2 = √

2

Í0w1

или

Í1 = Í0 + [ - Í2(w2/w1)].

(2.13)

Для наглядности уравнение (2.13) можно представить иначе:

Í1 = Í0 + Íк,

(2.14)

где Íк = -Í2(w2/w1) — нагрузочная составляющая тока первичной обмотки (компенсационный ток).

Таким образом, МДС, создаваемая током Iк, равна по величине и противоположна по фазе МДС вторичной обмотки, т. е. компенсирует МДС вторичной обмотки. Это обусловливает неизменность магнитного потока трансформатора. Векторная диаграмма идеализированного трансформатора, работающего под нагрузкой, показана на рис. 2.22,в. Мощность нагрузочной составляющей первичного тока равна мощности, отдаваемой трансформатором нагрузке, так как

IкE1cosφ2 = I2(w2/w1)E2(w1/w2)cosφ2 = I2E2cosφ2.

Следовательно, нагрузочная составляющая тока 1г не только уравновешивает МДС вторичной обмотки, но и обеспечивает поступление в трансформатор из сети мощности, отдаваемой приемнику электрической энергии, подключенному к вторичной обмотке.

Основные закономерности работы идеализированного трансформатора справедливы и для реальных трансформаторов.