§ 2.9. ИЗМЕНЕНИЕ ВТОРИЧНОГО НАПРЯЖЕНИЯ И ВНЕШНИЕ ХАРАКТЕРИСТИКИ

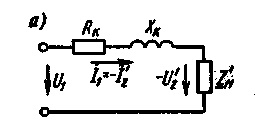
Изменение напряжения. Поскольку ток холостого хода в силовых трансформаторах большой и средней мощности сравнительно мал (0,5 — 3% от номинального), во многих случаях при расчетах используют упрощенную схему замещения (рис. 2.33,a) без намагничивающего контура. В этой схеме активные сопротивления R1 и R'2 первичной и вторичной обмоток соединены последовательно и образуют результирующее активное сопротивление Rк = R1 + R'2. Аналогично индуктивные сопротивле­ния Х1 и Х'2 образуют результирующее индуктивное сопротивление Хк = X1 + Х'2. Погрешность в определении первичного тока, вызванная таким упрощением, при нагрузках, близких к   номинальной,   составляет   примерно   0,1 %,   что   вполне допустимо.

Рис. 2.33. Упрощенная схема замещений трансформатора и ее векторная диаграмма при активноиндуктивной нагрузке

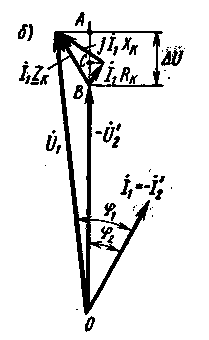Для упрощенной схемы замещения можно построить векторную диаграмму (рис. 2.33,6). В этой диаграмме вектор Í1Rк представляет собой результирующее активное падение напряжения в приведенном трансформаторе, вектор jÍ1Xк — результирующее реактивное падение напряжения, а вектор Í1Zк — результирующее полное падение напряжения. При этом

Í1Zк = Í1Rк + jÍ1Xк                                           (2.42)

Если известны значения uк.а, ик.р и ик,то полное падение напряжения в трансформаторе и его активная и реактивная составляющие:

I1Zк = βuкUном/100;        I1Rк = βик.аUном/100;         I1Xк = βuк.рUном/100,

где β = I2/I2ном ≈ I1/I1ном - коэффициент нагрузки.

Векторная диаграмма, представленная на рис. 2.33,6, позволяет также определить изменение напряжения трансформатора в зависимости от нагрузки. Обычно его рассчитывают при постоянном значении U1 = U1ном и номинальной частоте fном как отношение алгебраической разности значений вторичного напряжения при холостом ходе U20 и нагрузке U2 к напряжению U20 при холостом ходе и выражают в процентах:

Δи = (U20 - U2) 100/U20 = (U'20 - U'2) 100/U'20.                  (2.43)

Так как при холостом ходе отсутствуют падения напряжения в обмотках трансформатора, то U'20 = U1 и при номинальном значении U1 = U1ном

Δu = [(U1ном - U'2)/U1ном]100.

(2.44)

Из диаграммы (рис. 2.33,6) следует, что из-за малости угла φ1 - φ2 за модуль вектора Ú1 приближенно можно принять его проекцию на направление вектора — Ú'2, т. е. отрезок OA. Тогда ΔU = U1 - U'2 = OA - OB = BA.

Спроектировав аналогично векторы Í1Rк и jÍ1Xк на направление вектора Ú'2, получим

ΔU = BA = BC + CA = I1Rкcosφ2 + I1Xкsinφ2.

Таким образом, относительное изменение напряжения (%)

Δu =  [(I1Rкcosφ2+ I1Xкsin φ2)/Uном]100.

(2.45)

При номинальной нагрузке формула (2.45) принимает вид

Δuном =  [(IномRкcosφ2 + IномXкsin φ2)/Uном]100,

или

Δuном = ик.а cos φ2 + ик.р sin φ2.

Из (2.45) следует, что изменение напряжения трансформатора пропорционально току нагрузки I'2≈11 и зависит от угла φ2. Поэтому, используя понятие коэффициента нагрузки
β = I2/I2ном ≈ I1/I1ном, получаем

Δu = βΔuном = β(ик.аcosφ2+ ик.р sin φ2)

(2.46)

Более точная формула, используемая для силовых тран­сформаторов, имеет вид

Δu = β(uк.аcosφ2 + uк.рsinφ2) +

β2(uк.рcosφ2 - uк.аsinφ2)2 200

(2.47)

Однако и формула (2.46) дает результат, точность которого вполне приемлема в большинстве практически встречающихся случаев.

Внешние характеристики. Зависимость U2 = f(I2) или U2 = f(β) при U1 = U1ном = const, f = fном = const и cosφ2 = const называют внешней характеристикой трансформатора. Для ее построения можно использовать формулу

U'2 = U1ном(1 - Δu/100) = U1ном[1 - β(ик.аcosφ2+ик.рsinφ2)/100 - β2(ик.рcosφ2 - ик.аsin φ2)2/20000].

(2.48)

В пределах изменения коэффициента нагрузки β от 0 до 1 внешние характеристики практически прямолинейны (рис. 2.34, а).

Напряжение короткого замыкания ик, его составляющие ик.а и ик.р зависят в определенной степени от номинальной мощности трансформатора. В трансформаторах средней и большой

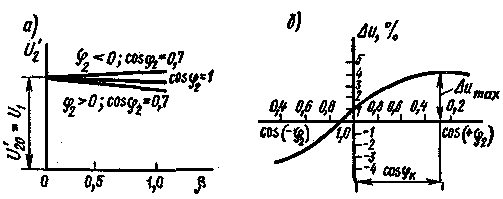Рис. 2.34. Внешние характеристики трансформаторов и график изменения Δu

мощности реактивная составляющая напряжения короткого замыкания значительно больше, чем активная. Поэтому в таких трансформаторах реактивная нагрузка вызывает большее изменение напряжения U'2, чем активная, т.е. чем меньше cosφ2, тем ниже проходит внешняя характеристика и значительнее изменяется напряжение U'2. При активно-индуктивнои нагрузке всегда напряжение U'2 < U1; при активно-емкостной нагрузке и некоторых углах φ2 оно может стать большим U1 [в формуле (2.48) при φ2<0 члены, содержащие sinφ2, становятся отрицательными]. При заданном значении β относительное изменение напряжения Δu зависит от величины угла φ2. При активной нагрузке величина Δu невелика; при активно-индуктивной нагрузке она возрастает и достигает максимального значения, когда φ2 = φк; при активно-емкостной нагрузке эта величина может стать отрицательной (рис. 2.34, б).

Характер изменения вторичного напряжения в трансформаторах средней и большой мощности (при Хк > Rк) при различных значениях угла φ2 показан на рис. 2.35. При φ2 > 0 (рис. 2.35, а) увеличение нагрузки приводит к довольно быстрому

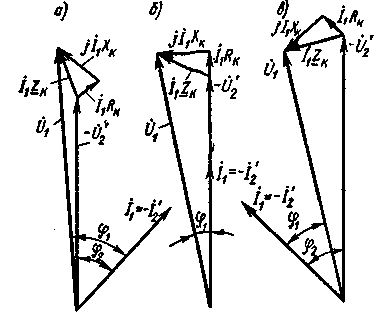Рис. 2.35. Упрощенные векторные диаграммы трансформатора при различных значениях угла φ2

возрастанию алгебраической разности ΔU = U1 — U'2. При φ2 = 0 (рис. 2.35,6) величина ΔU возрастает с увеличением нагрузки в значительно меньшей степени. При φ2 < 0 (рис. 2.35,в), т. е. когда ток I'2 опережает напряжение U'2 (активно-емкостная нагрузка), величина ΔU может изменить свой знак.

Изменение вторичного напряжения трансформатора при переменной нагрузке можно определить по диаграммам, приведенным на рис. 2.36. Если U1 = const и φ2 = const, а изменяется только ток I'2 (модуль вектора Í'2), то используется диаграмма (рис. 2.36, а). В этой диаграмме угол ВСЕ = (φк — φ2) = const. Как внешний угол треугольника ВСА он равен сумме углов ABC и CAB, которые опираются соответственно на дуги ВС и СА. Следовательно, и угол AFB также равен разности φк — φ2, так как он опирается на дугу ВСА. При изменении тока нагрузки I'2 изменяются стороны треугольника падения напряжений BCD и положение векторов Í1Zк и — Ú'2, но угол φк — φ2 остается неизменным. Следовательно, точка С перемещается по дуге ВСА окружности с диаметром BF = U1/[sin(φк — φ2)]. Изменение напряжения трансформатора ΔU = U1 — U'2определяется отрезком СЕ, отсекаемым на продолжении вектора  — Ú'2 дугой BE, проведенной из точки А радиусом АВ.
Если U1 = const и I'2 = const, а изменяется только угол φ2, то используется диаграмма (рис. 2.36,6). Для ее построения из точки О проводим полуокружность 1 радиусом OB = U1 а из точки О' — полуокружность 2 также радиусом О'С = U1 Так как треугольник OD'O' равен треугольнику падений напряжений BCD, то полуокружность 1 представляет собой геометрическое

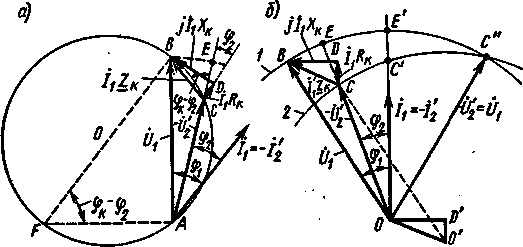Рис. 2.36. Круговые диаграммы трансформатора при перемен­ной нагрузке и U1 = const: о) — при  φ2 = const и  изменении  тока I'2;  б) — при  I'2 = const  и  изменении φ2

место концов вектора Ú1, а полуокружность 2 — геометрическое место концов вектора — Ú'2. Отрезки СЕ, расположенные меж ду этими полуокружностями, представляют собой изменения напряжения ΔU = U1 — U'2. Точки С' и Е' соответствуют режиму, при котором φ2 = 0, части окружностей 1 и 2, расположенные левее этих точек,— углам π/2 > φ2 > 0 (активно-индуктивная нагрузка), а части, расположенные правее этих точек,— углам — π/2 < φ2 < 0 (активно-емкостная нагрузка). В точке С", соответствующей некоторой активно-емкостной на грузке,   U1 = U'2   и   ΔU = 0.   В   области   правее   этой   точки U'2 > U1.

Уменьшение падения напряжения. Наличие индуктивных падений напряжения, вызываемых потоками рассеяния, ведет к не желательному изменению напряжения трансформатора под нагрузкой. Чтобы уменьшить потоки рассеяния, первичные и вторичные обмотки выполняют на одних и тех же стержнях, по возможности приближая одну обмотку к другой. При концентрической обмотке на характер магнитного поля потоков рассеяния (см. рис. 2.25,6) влияют токи обеих обмоток, и при режимах нагрузки, близких к номинальной, можно
считать, что Í1 = Í0 — Í2w2/w1 ≈ - Í2w2/w1 т. е. МДС первичной и вторичной обмоток равны по величине и находятся в противофазе. Поэтому сближение обмоток ведет к уменьшению потоков рассеяния.

Минимальное расстояние между обмотками ограничивается электрической прочностью изоляционного промежутка. Вследствие этого высоковольтные трансформаторы, в которых изоляционный промежуток больше, имеют относительно большие потоки рассеяния и напряжения короткого замыкания, чем низковольтные трансформаторы. При чередующейся обмотке (рис. 2.25, в) потоки рассеяния несколько больше, чем при концентрической.