§ 2.7. КОМПЛЕКСНЫЕ УРАВНЕНИЯ И ВЕКТОРНАЯ ДИАГРАММА

В реальном трансформаторе помимо основного магнитного потока Ф, замыкающегося по стали и сцепленного со всеми обмотками трансформатора, имеются также потоки рассеяния Ф_σ1 и Ф_σ2 (рис. 2.25), которые сцеплены только с одной из обмоток. Потоки рассеяния не участвуют в передаче энергии, но создают в каждой из обмоток соответствующие ЭДС самоиндукции
Е_σ1 = 4,44fw₁Ф_σ1m; E_σ2 = 4,44fw₂Ф_σ2m.
С учетом ЭДС самоиндукции и падений напряжения в активных сопротивлениях обмоток можно составить комплексные уравнения для первичной и вторичной обмоток трансформатора. С учетом (2.13) получим следующую систему уравнений:

Ú1 + É1 + Éσ1 = Í1R1; É2 + Éσ2 = Í2R2 + Í2Zн; Í1 = Í0 + ( - Í2w2/w1),

}

(2.20)

где Zh — сопротивление нагрузки, подключенной к трансформатору.

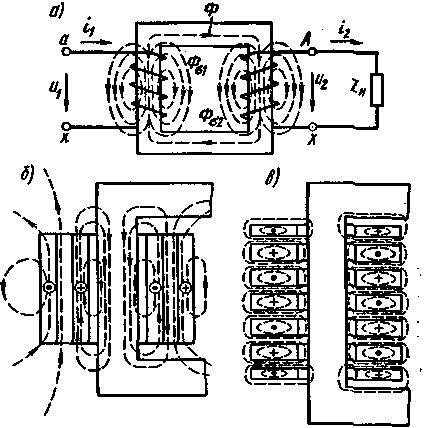Рис. 2.25. Схема магнитных потоков в трансформаторе [а)   и   распределение   потоков   рассеяния   при   концентрической (б) и чередующейся (в) обмотках

Поскольку потоки рассеяния полностью или частично замыкаются по воздуху, они пропорциональны МДС соответствующих обмоток или соответствующим токам:

E_σ1 = I₁X₁; E_σ2 = I₂X₂.                                         (2.21)

Величины X1 и Х2 называют индуктивными сопротивлениями обмоток трансформатора, обусловленными потоками рассеяния.

Так как векторы ЭДС Е́_σ1 и Е́_σ2 отстают от соответствующих потоков и токов на 90^o,то

Éσ1 = -jÍ1X1; Éσ2 = -jÍ2X2.                                         (2.22)

При этом комплексные уравнения трансформатора примут вид

Ú1 + É1 = Í1R1 + jÍ1X1 = Í1Z1;

(2.23)

É2 + Í2R2 + jÍ2X2 + Í2Zн = Í2Z2 + Í2Zн;

(2.24)

Í1 + ( -Í2w2/w1) = Í0.

(2.25)

Замена ЭДС Éσ1 и Eσ2 падениями напряжений -jÍ1X1 и -jÍ2X2 наглядно показывает роль потоков рассеяния:  они создают индуктивные  падения   напряжения  в  обмотках,  не участвуя   в  передаче   энергии   из   одной   обмотки   в   другую.

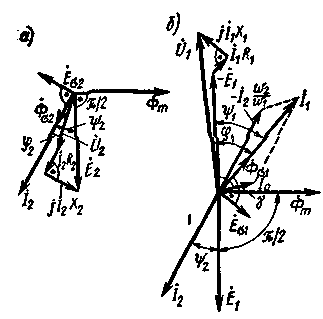Рис.  2.26.   Векторные   диаграммы обмоток трансформатора при активно-индуктивной нагрузке

Проще становится и построение векторной диаграммы, соответствующей системе уравнений (2.23) - (2.25), в которой целесообразно также заменить  паление  напряжения  в  нагрузке величиной U2 = I2Zн, т.е. вторичным напряжением трансформатора, определяемым из (2.24):

Ú2 = É2 - Í2R2 - jÍ2X2.

(2.26)

Векторную диаграмму вторичной обмотки трансформатора (рис. 2.26, а) строят согласно уравнению (2.26). Характер диаграммы определяется током нагрузки I2, который принимается заданным по величине и фазе. Иными словами, задаваясь векторами  вторичных тока I2 и напряжения U2, можно построить вектор ЭДС

É2 = Ú2 + Í2R2 = jÍ2X2,                        (2.27)

   

если известны параметры трансформатора. Вектор I2R2 параллелен вектору тока I2, а вектор jI2X2 опережает вектор ЭДС E2 на 90о. Векторную  диаграмму  первичной  обмотки  трансформатора (рис. 2.26,6) строят в соответствии с уравнением

Ú1 = -É1 + Í1R1 + jÍ1X1.

(2.28)

Построение диаграммы начинают с вектора потока Ф́0, который создается током холостого хода Í0, Этот ток опережает вектор потока Ф́m на угол γ = 5÷10о. Вектор ЭДС É1, как и É2, отстает от потока Ф́m на угол 90о. Ток в первичной обмотке трансформатора Í1 = Í0 + (-Í2w2/w1), поэтому на рис 2.26,б нужно показать и вектор тока Í2, сдвинутый на угол ψ2 относительно вектора É1 (векторы É1 и É2 совпадают по направлению). Зная Í2, можно изобразить вектор -Í2w2/w1 и получитьь вектор Í1 как сумму векторов Í0 и -Í2w2/w1.

Найдя вектор тока Í1, можно определить значения векторов Í1R1 и jÍ1X1 и построить искеомый вектор напряжения Ú1 как сумму трех составляющих: векторов -É1 и падений напряжений в обмотках Í1R1 и jÍ1X1.

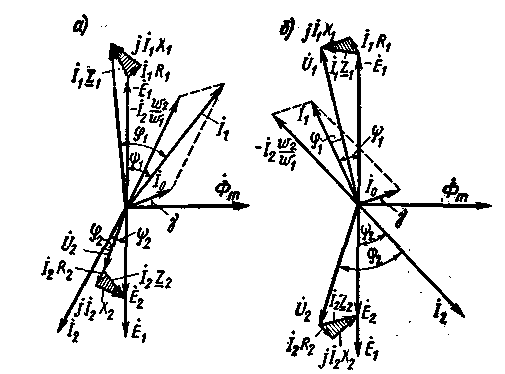Рис. 2.27. Полные векторные диаграммы трансформатора при активно-индуктивной (а) и активно-емкостной (б) нагрузках

Целесообразнее строить общую диаграмму трансформатора для его первичной и вторичной обмоток (рис. 2.27,а,б), хотя эти обмотки и не связаны между собой электрически.