§ 3.4. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ

Пульсирующее поле. При питании однофазной обмотки переменным током возникает магнитное поле, пульсирующее во времени с частотой изменения тока. В этом случае при синусоидальном распределении МДС (рис. 3.12) в каждой точке воздушного зазора, расположенной на расстоянии х от оси обмотки, действует МДС

где F0 = Fm sin ωt - МДС в точке, расположенной на оси обмотки.

Выражение (3.14) можно преобразовать к виду

Каждый из членов правой части (3.13) представляет собой уравнение бегущей (или вращающейся) волны МДС. Следовательно, пульсирующее магнитное поле, синусоидально распределенное в пространстве, можно представить в виде суммы двух магнитных полей, вращающихся в противоположных направлениях (рис. 3.13). При этом бегущие волны МДС, создающие эти магнитные поля,

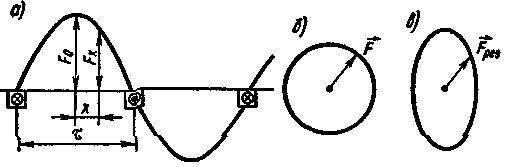Рис.  3.12.  Диаграмма  распределения  МДС  в  воздушном зазоре (а) и годографы пространственного вектора МДС (б, в)

Рис.  3.13.  Вращающиеся магнитные поля однофазной обмотки

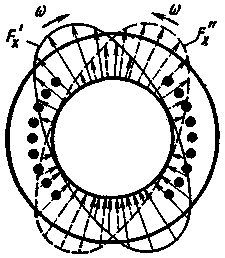В каждом из этих полей максимальные значения МДС в различные моменты времени остаются неизменными. Следовательно, если каждое из этих полей представить в виде пространственного вектора МДС F (рис. 3.12,6), то конец его будет описывать окружность. Такое поле называют круговым.

В качестве положительного направления условно примем направление вращения бегущей волны МДС по часовой стрелке. Координату точки х, в которой МДС F'x максимальна и равна 0,5Fm, можно получить, положив sin (ωt - πx/τ) = 1. При этом ωt - πx/τ = π/2, откуда

Следовательно, при увеличении угла ωt координата точки х перемещается в положительном направлении, т. е. МДС F'x вращается по часовой стрелке, a F''x — против часовой стрелки. Линейная скорость перемещения бегущей волны МДС

т. е. за один период магнитное поле проходит пару полюсов. Частота вращения бегущей волны МДС (частота вращения магнитного поля)

Следовательно, изменяя число полюсов электрической ма-шины 2р, можно получать различные частоты вращения магнитного поля.

Из (3.17) следует, что в многополюсной машине за один период изменения переменного тока магнитное поле поворачивается на пространственный угол 360°/р, соответствующий одной паре полюсов. Поэтому при рассмотрении электромагнитных процессов в электрических машинах вводят понятие «электрические градусы», с которыми оперируют при построении векторных диаграмм, проектировании обмоток и пр. При этом 360 временным градусам соответствует 360р электрических градуса, а электрические градусы имеют связь с геометрическими градусами в виде соотношения α°эл = рα°геом.

Круговое вращающееся поле при трехфазной обмотке. Если на статоре электрической машины расположить симметричную трехфазную обмотку (рис. 3.14), у которой оси фаз АХ, BY и CZ сдвинуты в пространстве на угол 120°, то при питании ее симметричным трехфазным током получим круговое вращающееся магнитное поле. На рис. 3.14 для простоты фазы обмотки показаны сосредоточенными, но распределение МДС, образуемое каждой фазой, следует считать синусоидальным.

Рис.   3.14.   Расположение обмоток фаз на статоре двухполюсной трехфазной машины

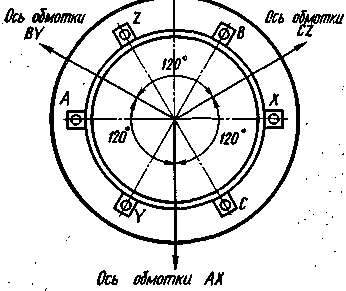Ввиду того что в рассматриваемой обмотке фазы АХ, BY и CZ смещены в пространстве на (2/3) τ, а токи в них сдвинуты во времени на угол (2/3) π, получим следующие выражения для составляющих МДС в точке х от каждой из фаз:

FxA = Fm sin ωt cos

πx τ

=

Fm 2

sin (ωt -

πx τ

) +

Fm 2

sin (ωt +

πx τ

);

FxB = Fm sin (ωt -

2π 3

) cos (

πx _ 2π τ   3

) =

Fm 2

sin(ωt -

πx τ

) +

Fm 2

sin (ωt +

πx _ 4π τ   3

);

FxC = Fm sin (ωt -

4π 3

) cos (

πx _ 4π τ   3

) =

Fm 2

sin(ωt -

πx τ

) +

Fm 2

(ωt +

πx τ

+

4π 3

).

Результирующую МДС в точке х можно получить путем сложения отдельных ее составляющих FxA, FxB, FxC. При этом обратновращающиеся волны МДС исчезают, а результирующая МДС

Круговое вращающееся поле при двухфазной обмотке. В симметричной двухфазной обмотке фазы АХ и BY (рис. 3.15, а) сдвинуты в пространстве на половину полюсного деления τ. Если такую обмотку питать симметричным двухфазным током, при котором токи отдельных фаз ÍА и ÍВ (рис. 3.15,6) сдвинуты во времени на угол 90° (ÍВ = ± jÍА ) то возникает круговое вращающееся поле.

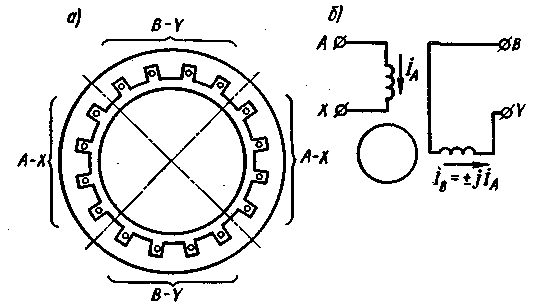Рис. 3.15. Схема двухполюсной двухфазной машины и расположение на статоре обмоток ее фаз

Для составляющих МДС, образуемых этими токами, получим следующие выражения:

FxA = Fm sin ωt cos

πx τ

=

Fm 2

sin(ωt -

πx τ

) +

Fm 2

sin(ωt

+

πx τ

);

FxB = Fmsin(ωt -

π 2

)cos(

πx _ π τ   2

) =

Fm 2

sin(ωt -

πx τ

) +

Fm 2

sin(ωt +

πx τ

- π);

При этом уравнение бегущей волны принимает вид

Частота вращения поля, образованного двухфазной обмоткой, определяется так же, как и поля, образованного трехфазной обмоткой, по формуле (3.17). Для изменения направления вращения поля следует изменить порядок чередования тока в фазах обмотки, т. е. переключить провода, присоединяющие фазы обмотки к сети. Общий случай кругового вращающегося поля. В общем случае, когда по симметричной m-фазной обмотке (фазы которой сдвинуты в пространстве на угол α = 2π/т) проходят переменные токи, сдвинутые во времени на угол 2π/т, уравнение бегущей волны МДС имеет вид

Несимметричная m-фазная обмотка также может создать круговое вращающееся поле, если на ее фазы подать определенным образом подобранную m-фазную несимметричную систему токов. Однако на практике фазы многофазных обмоток обычно располагают симметрично, чтобы получить круговое поле при минимальных токах в фазах и электрических потерях в них.

Круговое вращающееся магнитное поле обладает следующими характерными свойствами:

а)  максимумы результирующих волн МДС и индукции всегда совпадают с осью той фазы, в которой ток имеет максимум. Это положение легко проверить, задаваясь величиной ωt, соответствующей максимуму тока в фазе, и определяя по (3.15) координату точки х, в которой МДС F'x максимальна;

б)  магнитное поле перемещается в сторону оси той фазы, в которой ожидается ближайший максимум. Это свойство непосредственно следует из предыдущего;

в)  для изменения направления вращения поля необходимо изменить порядок чередования тока в фазах. В трехфазных машинах для этого следует поменять местами провода, подводящие ток из трехфазной сети к двум любым фазам обмотки. В двухфазных машинах нужно переключить провода, присоединяющие фазы обмотки к двухфазной сети.

Эллиптическое поле. Круговое вращающееся магнитное поле возникает при симметрии токов, проходящих по фазам (симметрии МДС катушек отдельных фаз), симметричном расположении этих фаз в пространстве, сдвиге во времени между фазными токами, равном пространственному сдвигу между фазами и синусоидальном распределении индукции в воздушном зазоре машины вдоль окружности статора (ротора). При несоблюдении хотя бы одного из указанных условий возникает не круговое, а эллиптическое вращающееся поле, у которого максимальное значение результирующей МДС и индукции для различных моментов времени не остается постоянным, как при круговом поле. В таком поле пространственный вектор МДС описывает эллипс (см. рис. 3.12, в).

Эллиптическое поле можно представить в виде двух эквивалентных круговых полей, вращающихся в противоположных направлениях. Поле, вращающееся по направлению вращения результирующего эллиптического поля, называют прямым; поле, вращающееся в противоположном направлении,— обратным. Разложение эллиптического поля на прямое и обратное круговые поля производят методом симметричных составляющих, с помощью которого определяют МДС прямой иобратной последовательностей.

 

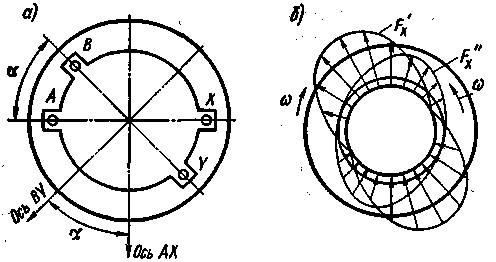Рис. 3.16. Расположение обмоток фаз на статоре несимметричной двухфазной машины (а) и вращающиеся магнитные поля при несимметричном их питании (б)

Рассмотрим, например, двухфазную машину, у которой на статоре расположены две фазные обмотки (фазы) АХ и BY, оси которых смещены в пространстве на некоторый угол α (рис. 3.16, а). Токи, проходящие по этим фазам, и соответствующие векторы МДС FxA и FxB сдвинуты во времени на некоторый угол β. Фазы АХ и BY создают пульсирующие магнитные поля, синусоидально распределенные в пространстве. МДС этих фаз, действующие в любой точке х воздушного зазора,

МДС фаз АХ и BY аналогично (3.15) можно представить в виде суммы двух бегущих волн МДС противоположных направлений:

В выражениях (3.21) складываются или вычитаются временные и пространственные углы, т. е. они становятся эквивалентными. Это объясняется тем, что пространственное положение вектора МДС вращающегося поля определяется временем и частотой тока, питающего фазы, — за один период поле перемещается на пару полюсов. Результирующее магнитное поле, создаваемое совместным действием двух обмоток, можно получить путем сложения составляющих векторов МДС прямой последовательности, вращающихся по часовой стрелке (образующих прямое поле):

а также векторов МДС обратной последовательности, вращаю-щихся против часовой стрелки (образующих обратное поле)

F"xA = 0,5FmA sin (ωt + πx/τ) и F"xB = 0,5FmB sin (ωt + β + πx/τ

− +

α).

Суммарные МДС полей, вращающихся в противоположные стороны, т. е. F'x = F'xA + F'xB и F''x = F"xA + F"xB, не равны по величине (рис. 3.16,6), а поэтому результирующее поле машины не пульсирующее, а вращающееся. В этом поле максимальное значение результирующей МДС в различные моменты времени не остается постоянным, как при круговом поле, т. е. поле эллиптическое. В двухфазной машине можно также получить и круговое вращающееся поле; при этом одна из составляющих МДС F'x или F"x должна отсутствовать. Условия получения кругового поля в такой машине сводятся к взаимной компенсации одной из пар МДС F'xA и F'xB или F"xA и F"xB. Последнее может быть, если указанные МДС равны по амплитуде, но противоположны по фазе, т. е. если α ± β = π.