§ 3.7. МЕТОДЫ РАСЧЕТА МАГНИТНОЙ ЦЕПИ ЭЛЕКТРИЧЕСКИХ МАШИН

Принципы расчета. Расчет магнитной цепи вращающихся электрических машин основан на тех же принципах, что и расчет магнитной цепи трансформатора; его цель - найти связь между величинами магнитного потока и тока обмотки, которая создает этот поток.

Различие между магнитными расчетами трансформатора и вращающейся машины определяется разницей в конструкциях: в машине имеется воздушный зазор между статором и ротором, который главным образом и определяет магнитное сопротивление; кроме того, машина имеет более сложную конфигурацию отдельных частей магнитопровода (зубцов ротора и статора и т. д.).

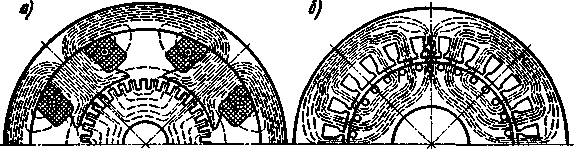
Магнитный поток в электрических машинах может созда­ваться обмотками, по которым проходит переменный ток (асинхронные машины) или постоянный ток (синхронные машины и машины постоянного тока). Эти обмотки могут быть сосредоточенными или распределенными по окружности статора или ротора. Соответственно различают машины с явновыраженными (рис. 3.27, а) и неявновыраженными (рис. 3.27,6) полюсами.

При холостом ходе магнитное поле многополюсной машины симметрично, т. е. магнитные потоки всех полюсов одинаковы, и их магнитные линии проходят через одинаковые участки магнитной цепи. Это позволяет вести расчет на пару полюсов.

Расчет магнитной системы машин переменного и постоянного   тока   проводят   по   одной   и   той   же

Рис.  3.27.  Магнитные поля электрических  машин  с  явновыраженными (а) и неявновыраженными (б)

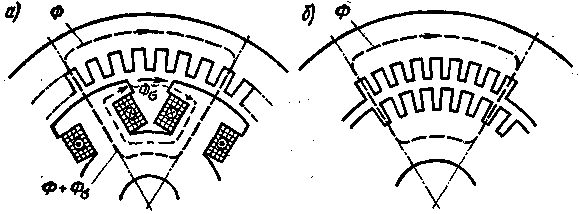
Рис. 3.28. Расчетные схемы магнитной системы электрической машины

методике на основании закона полного тока. МДС обмотки, создающей магнитный поток возбуждения, определяют для части магнитной системы, ограниченной двумя осями симметрии полюсов.

В машинах с явновыраженными полюсами (рис. 3.28, о) магнитную цепь разбивают на характерные участки: воздушный зазор, зубцовый слой, сердечники полюсов, ярма статора и ротора.   В  данном   случае   закон   полного   тока  имеет   вид

где FB — МДС (на пару полюсов) обмотки, создающей магнитный поток возбуждения; Fδ, Fz, Fm, Fa1, Fa2 — магнитные напряжения соответственно в воздушном зазоре, зубцовом слое, сердечниках полюсов, ярмах статора и ротора.

В машинах с не явновыраженными полюсами в магнитной системе отсутствуют сердечники полюсов, но имеются два зубцовых слоя на статоре и роторе (рис. 3.28,6). При этом

где Fz1 и Fz2 — магнитные напряжения в зубцовых слоях статора и ротора.

Ниже приведена методика определения магнитных напряжений на каждом из участков магнитной цепи.

Магнитное напряжение в воздушном зазоре. При неизменном воздушном зазоре между ротором (или статором) и сердечником полюса (что является характерным для многих синхронных машин и машин постоянного тока) распределение индукции в воздушном зазоре имеет вид криволинейной трапеции 1 (рис. 3.29, а). При определении магнитного напряжения в зазоре действительное распределение индукции заменяют прямоугольным 2, предполагая индукцию неизменной на некоторой теоретической дуге bi. Дуга bi должна быть выбрана так, чтобы поток полюса, пропорциональный площади, ограничиваемой кривой индукции, остался неизменным. Обычно bi

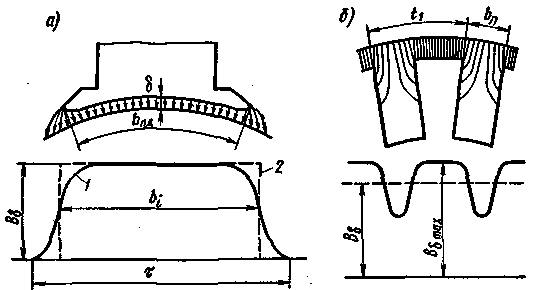Рис. 3.29. Кривые распределения магнитной индукции в воздушном зазоре при гладком и зубчатом якоре

мало отличается от конструктивной длины полюсной дуги bпд: при равномерном воздушном зазоре можно считать, что bi = bпд + 2δ (где δ - воздушный зазор), а при полюсном наконечнике со скошенными краями bi ≈ bпд. Отношение αi = bi /τ называют коэффициентом полюсного (магнитного) перекрытия.

Магнитное напряжение в воздушном зазоре определяют по Значению потока, проходящего через зазор из статора в ротор (или наоборот):

где li - продольная расчетная (активная) длина воздушного зазора; Вδ - индукция в воздушном зазоре (при номинальном режиме она изменяется от 0,6 до 1,1 Тл, причем большие значения соответствуют машинам большей мощности).

Из формулы (3.26) следует, что при заданной индукции Вδ в воздушном зазоре с увеличением коэффициента полюсного перекрытия αi возрастает и магнитный поток Ф. Однако при значительном увеличении αi сильно возрастает поток рассеяния Фσ, который замыкается через ярмо и сердечники полюсов, минуя якорь (см. рис. 3.28, а). Обычно αi = 0,6 ÷ 0,8, причем меньшие значения соответствуют машинам меньшей мощности.

Напряженность магнитного поля в воздушном зазоре

а магнитное напряжение (на два воздушных зазора) где Lδ = δi — длина отрезка расчетной магнитной линии в воздушном зазоре.

При наличии зубцов на роторе или статоре длина расчетной магнитной линии в зазоре δi больше расстояния δ между ротором и статором, так как магнитные линии в зазоре искривлены (см. рис. 3.29,6). Это обстоятельство учитывается путем введения в расчет некоторого коэффициента kδ, называемого коэффициентом воздушного зазора или коэффициентом Картера (по имени английского ученого, впервые установившего количественную связь между средней длиной магнитной линии в зазоре и конфигурацией зубцового слоя), поэтому δi = kδ δ.

Значение kδ при наличии зубцов только на роторе или статоре машины можно определить по формуле kδ = t1/(t1 — γδ), где t1 -зубцовое деление; γ = (b0/δ)2/(5 + b0/δ) при b0/δ > 1; b0 — ширина шлица паза (при полузакрытых и полуоткрытых пазах); при открытых пазах b0 принимают равным ширине паза bп.

Если зубцы имеются на роторе и статоре (асинхронные машины, машины постоянного тока с компенсационной обмоткой, синхронные машины с успокоительной обмоткой), то

где kδ1 и kδ2 - коэффициенты воздушного зазора для ротора и статора.

При определении индукции Вδ и напряженности Hδ магнитного поля в воздушном зазоре расчетную (активную) длину зазора следует вычислять с учетом различных конструктивных длин статора lа1 и ротора lа2 (рис. 3.30, а) и наличия радиальных вентиляционных каналов (рис. 3.30,6). Обычно принимают, что расчетная длина li = 0,5 (lа1 + lа2). При наличии в роторе или статоре nк вентиляционных каналов шириной bк за эквивалентную длину соответствующей части машины принимают l'а = l — 0,5nк bк, где l — конструктивная длина этой части.

Зависимость величины Fδ от индукции Вδ (или от Ф)

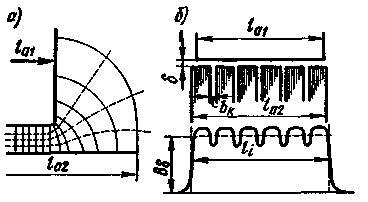Рис. 3.30. Кривые распределения магнитной индук­ции в воздушном зазоре у краев ротора и статора и при наличии радиальных вентиляционных каналов

является линейной, так как μ0 = const. Обычно при номинальном режиме работы машины Fδ = (0,7 ÷ 0,9)FB.

Магнитное напряжение в зубцовом слое. В зубцах ротора и статора индукция значительно больше, чем в воздушном зазоре. В слое, прилегающем к воздушному зазору,

где γ = 0,9 ÷ 0,93 - коэффициент заполнения объема якоря сталью, учитывающий наличие изоляции между листами, bz — ширина зубца в данном месте.

При полузакрытых пазах овальной или трапецеидальной формы (рис. 3.31, а) зубцы имеют параллельные стенки, вследствие чего индукция Bz неизменна по всей высоте зубца. В таком зубце постоянна и напряженность Магнитного поля Hz, которая определяется по подсчитанному значению Вz на основании кривой намагничивания для данной марки стали.

При прямоугольных пазах зубцы приобретают клинообразную форму, при которой индукция в зубцах увеличивается по мере приближения к основанию паза ротора (рис. 3.31,6) и к головке зубца статора (рис. 3.31, в).

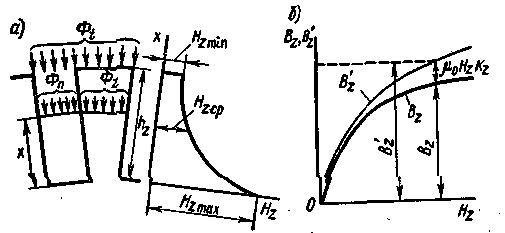
При определении магнитного напряжения в зубцовом слое, когда индукция в зубцах превышает 1,8 Тл, следует учитывать, что поток Фt зубцового деления (pис. 3.32, а) из-за большого магнитного насыщения зубцов делится на две части, одна из которых (зубцовый поток Фz) проходит через зубец, а вторая (пазовый поток Фп) — через паз. При этом для любого сечения зубцового слоя на расстоянии х от дна паза

Разделим обе части (3.31) на площадь Szx поперечного сечения зубца в данном месте (за вычетом площади изоляционных прокладок между листами):

При этом Фzx и Фпx изменяются по высоте зубца с изменением площади Szx и условий насыщения.

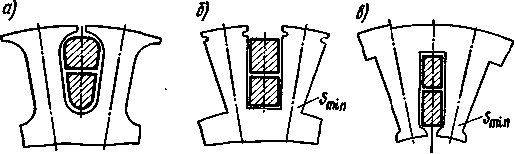Рис. 3.31. Зубцовые слои ротора и статора

Рис. 3.32.   Кривые   распределения   магнитных   потоков в зубцовом слое (а) и построение зависимостей (б): Вz =f(Нz )и В'z =f(Нz)

Величину Фt/Szx = B'zx можно рассматривать как некоторую фиктивную (расчетную) индукцию в зубце. Действительная индукция в зубце Bzx = Фzx /Szx, а индукция в пазу Bпх = Фпх/Sпх; следовательно,

где kz = Sпх/Szx — зубцовый коэффициент, зависящий от геометрических размеров зубца и паза в данном сечении; Нпх -напряженность магнитного поля в пазу на расстоянии х от дна.

Таким образом,

Практически напряженность магнитного поля в пазу мало изменяется по ширине паза и, следовательно, можно принять что на любом расстоянии х от дна паза напряженности магнитного поля в пазу Нпх и в зубце Hzx одинаковы. Это допущение позволяет весьма просто получить зависимость между pacчетной индукцией и напряженностью магнитного поля в зубцах (рис. 3.32,6). Задаваясь напряженностью магнитного поля в зубце Hzx, по кривой намагничивания стали можно построить график действительной индукции в зубце Bz = f(Hz ), а затем по формуле (3.32) - график расчётной индукции Bz = f(Hz) для некоторого постоянного значения kz.

Практически напряженность поля в зубцах Hz определяют по номограмме (рис. 3.33), построенной для всех встречающих¬ся на практике значений kz. Чтобы найти магнитное напряжение в зубцовом слое, зубец разделяют по высоте на несколько участков величиной Δhz и для каждого участка вычисляют индукцию Bz, B'z и напряженность Hz. Затем строят кривую изменения напряженности поля Hz вдоль высоты зубца (рис. 3.32, а) и вычисляют магнитное напряжение

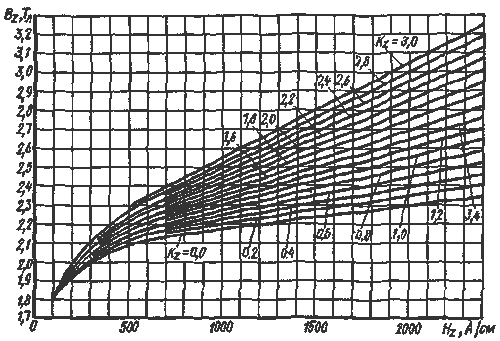Рис. 3.33. Номограмма для определения напряженности Hz магнитного поля в зубцах, выполненных из электротехнической стали по значению расчетной индукции B'z (сталь горячекатаная)

При расчете Fz за величину Szx принимают только площадь, приходящуюся на стальные листы (не учитывая изоляционные прокладки между ними). При клинообразных зубцах на различных участках зубца из-за изменения Szx изменяется не только расчетная индукция B'z но и коэффициент kz.

Часто используют упрощенный прием, при котором в качестве расчетной эквивалентной напряженности магнитного поля в зубце Нz экв принимают ее значение, вычисленное по формуле Симпсона для трех сечений (верхнего, нижнего и среднего):

При этом

В ряде случаев за эквивалентную расчетную величину напряженности магнитного поля в зубце Нz экв принимают ее значение для сечения зубца, расположенного на 1/3 его высоты (считая от наиболее узкого места). Естественно, что этот способ является менее точным.

Обычно для машин переменного тока общепромышлен­ного исполнения при номинальном режиме индукция в зубцах с параллельными стенками Bz = 1,4 ÷ 1,8 Тл; в клиновидных зубцах Bz max= 2,0 ÷ 2,2 Тл. В машинах постоянного тока эти значения обычно выше на 5 — 10%.

Магнитное напряжение в полюсах, ярмах ротора и статора. В машинах с явновыраженными полюсами расчетный магнитный поток в ярмах ротора и статора может иметь различные значения в зависимости от места установки полюсов. Если полюсы расположены на роторе (обычно у синхронных машин), через них и ярмо ротора замыкается не только полезный поток Ф, но и поток рассеяния Фσ. Поэтому для полюсов и ярма ротора расчетным потоком является суммарный поток:

где σ = 1 + Фσ/Ф — коэффициент магнитного рассеяния.

Для ярма статора (якоря) расчетным потоком является поток Ф.

Если полюсы расположены на статоре (обычно у машин постоянного тока), расчетным потоком для них и ярма статора является поток σФ, а для ярма ротора — поток Ф. Определение потока рассеяния Фσ в явнополюсных машинах является весьма сложной задачей, которая решается достаточно точно путем построения картины магнитного поля. Обычно коэффициент рассеяния σ = 1,1 ÷ 1,2.

Чтобы найти магнитные напряжения Fа1 и Fa2 в ярмах статора и ротора, необходимо построить для них картины магнитного поля, так как магнитный поток, проходящий через различные сечения вдоль средней магнитной линии ярма, в общем случае неодинаков. Например, при распределенной обмотке (в асинхронных двигателях) наибольший поток в ярмах статора и ротора имеется в среднем сечении 1 - 1 (рис. 3.34, а). Такое же распределение потока характерно для статоров синхронных машин и роторов машин постоянного тока. В статорах машин постоянного тока и роторах явнополюсных синхронных машин поток по длине средней линии ярма изменяется мало.

При практических расчетах часто пренебрегают неравномерностью распределения магнитного поля в ярмах статора и ротора и принимают, что индукция в них постоянна по всему сечению и неизменна вдоль средней магнитной линии ярма. В этом случае магнитные напряжения Fа1 и Fa2 определяют путем вычисления магнитных индукций Ва1 и Ва2 и установления расчетных длин средних магнитных линий La1 и La2

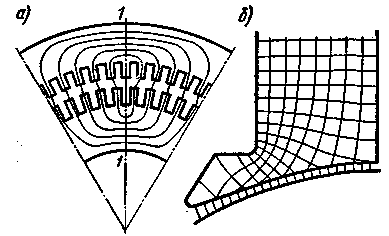Рис. 3.34. Магнитные поля в ярмах статора и ротора и в полюсе

для этих частей машины (они определяются по геометрическим размерам статора и ротора без учета поперечного сечения вала): где Ha1 и На2 — напряженность магнитного поля в ярмах статора и ротора, которые принимаются постоянными.

Некоторая неточность при определении магнитных напря-жений Fa1 и Fa2 без построения картин поля мало влияет на МДС Fв, так как индукция в ярмах ротора и статора невелика. Обычно она равна 1,2 — 1,4 Тл и магнитное напряжение в них составляет 5 — 10% от величины Fв.

Магнитное поле в сердечнике полюса также распределено довольно равномерно (рис. 3.34,6), и можно считать, что индукция Вт и напряженность в нем магнитного поля Нт постоянны вдоль высоты hm, а расчетная длина магнитной линии равна hm. При этом

При номинальном режиме индукция в сердечниках полю-сов составляет Вт= 1,3 ÷1,6 Тл. Однако в некоторых случаях в полюсных наконечниках могут иметься значительные насыщения, влияющие на распределение магнитного потока в воздушном зазоре под краями полюсов.

Ток возбуждения и намагничивающий ток. Если магнитный поток машины создается обмоткой возбуждения, питаемой постоянным током, то необходимый ток возбуждения определяется по известному значению МДС величины Fв на пару полюсов:

где wв — число витков обмотки возбуждения.

При создании магнитного потока многофазной Обмоткой, питаемой переменным током, необходимый намагничивающий ток в фазе

где wф и ko6.ф — число витков в фазе и обмоточный коэффициент данной обмотки; m - число фаз.

Магнитная характеристика. На рис. 3.35, а приведена типичная магнитная характеристика Ф = f(Fв) в относительных единицах для электрических машин с явновыраженными полюсами (синхронных машин и машин постоянного тока). Ее можно построить по результатам расчета магнитной системы машины при различных значениях магнитного потока. На магнитной характеристике резко выражен начальный прямолинейный участок, что обусловлено наличием сравнительно большого воздушного зазора, для которого характерна линейная зависимость магнитного напряжения от магнитного потока Ф. При сравнительно малых значениях магнитного потока, а следовательно, и магнитной индукции в ферромагнитных участках магнитной системы магнитными напряжениями на этих участках можно пренебречь и считать, что Fв ≈ Fδ. По мере увеличения магнитного потока магнитные сопротивления участков возрастают, особенно сильно зубцового слоя. При индукции в зубцах, примерно равной 1,6 Тл, зависимость Ф = f(Fв ) начинает отклоняться от прямолинейной.

В большинстве электрических машин точку а, соответствующую номинальному режиму, выбирают на криволинейном участке магнитной характеристики; при работе на линейном участке (т. е. при небольшой магнитной индукции) плохо используется сталь магнитной системы, а при больших

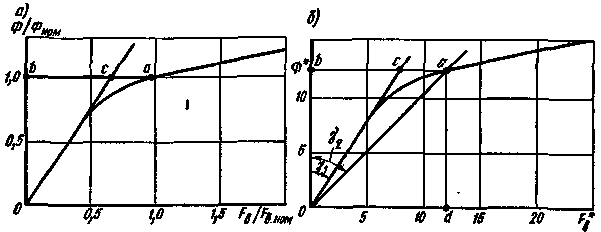Рис. 3.35. Магнитные характеристики электрических машин

насыщениях резко возрастает МДС обмотки, создающей магнитный поток, а следовательно, число витков этой обмотки и поперечное сечение провода. Таким образом, ненасыщенная машина и машина с большим насыщением магнитной системы требуют повышенного расхода активных материалов.

Количественно степень насыщения магнитной системы харак¬теризуется коэффициентом насыщения kнас, который можно найти из магнитной характеристики (рис. 3.35, а) как отношение отрезка ab, соответствующего МДС Fв ном, к отрезку bс, отсекаемому продолжением прямолинейного участка магнитной характеристики. Для машин переменного тока kнас = 1,1 ÷ 1,3; для машин постоянного тока kнас = 1,4 ÷ 1,8. Применение несколько меньших коэффициентов насыщения в синхронных машинах по сравнению с машинами постоянного тока объясняется стремлением уменьшить магнитные потери в стали якоря и сократить число витков обмотки возбуждения.

Магнитные характеристики различных машин с одинаковыми коэффициентами насыщения, выраженные в относительных единицах, практически совпадают. Это означает, что все многообразие магнитных характеристик можно свести к одной кривой, выраженной в некоторых условных единицах. Такая универсальная кривая, полученная из магнитной характеристики реальной машины, изображена на рис. 3.35,6 и соответствует приведенным ниже цифрам:

Ф*. . . . . . . .	3	5	7	9	10	11	12	13	14	15
Fв*. . . . . . . .	1.9	3.2	4.5	5.9	6.9	8.2	10.6	15.0	20.0	25.0

Если требуется построить магнитную характеристику для машины, имеющей, например, kнас = 1,5, то поступают следующим образом. На универсальной магнитной характеристике (рис. 3.31,6) из начала координат проводят вспомогательную прямую, образующую с осью ординат угол γ2, тангенс которого в 1,5 раза больше тангенса угла γ1, образуемого прямолинейной частью универсальной магнитной характеристики с той же осью. Вспомогательная прямая пересекает универсальную характеристику в точке а, которая и соответствует номинальному режиму, т. е. в данном случае Ф*ном = 12,3 (точка b) и F*в.ном = 11,85 (точка d).

В соответствии с полученными значениями Ф*ном и F*в.ном можно перестроить универсальную магнитную характеристику в характеристику, выраженную в относительных единицах с kнас = 1,5, используя формулы Ф/Фном = Ф*/Ф*ном и Fв/Fв.ном = F*в/F*в.ном. Построенные таким способом расчетные кривые дают погрешность не более 3%.