§ 4.4. РАБОТА АСИНХРОННОЙ МАШИНЫ ПРИ ВРАЩАЮЩЕМСЯ РОТОРЕ

ЭДС и ток в обмотке ротора. Рассмотрим общий случай индуцирования ЭДС в обмотке ротора, увлекаемого вращающимся магнитным полем. Так как эта обмотка пересекается магнитным потоком с частотой пs = п1 - п2 , частота индуцируемой в ней ЭДС

Учитывая, что pп1 /60 = f1 и (п1 - п2 )/п1 = s, представим (4.12) в ином виде:

При вращении ротора ЭДС в его обмотке

Учитывая, что ЭДС при заторможенном роторе Е2 = 4,44f1 w2 kоб2 Фm, получаем

Если обмотка ротора замкнута, по ней проходит ток с частотой f2 , который создает бегущую волну МДС F2 ; вращающуюся относительно ротора с частотой

Направление вращения МДС ротора определяется порядком чередования максимумов тока в фазах, т. е. МДС ротора вращается в ту же сторону, что и магнитное поле статора (см. § 3.4). Легко заметить, что частота вращения МДС ротора относительно статора равна сумме частот п2 + nF2 = п1.

Следовательно, при вращении ротора МДС cтamopa F1 и МДС ротора F2 вращаются в пространстве с одинаковой частотой, т. е. относительно друг друга они неподвижны. Таким образом, полученные выше для заторможенного ротора выводы о взаимодействии токов в первичной и вторичной обмотках применимы и для вращающегося ротора.

Из изложенного следует, что в асинхронной машине магнитное поле, вращающееся с частотой n1, возникает в результате совместного действия бегущих волн МДС ротора и статора. Оно служит связующим звеном между статором и ротором, обеспечивая обмен энергией между ними, точно так же, как переменное магнитное поле в трансформаторе осуществляет передачу энергии из первичной обмотки во вторичную.

Энергетическая диаграмма. При работе асинхронной машины в двигательном режиме (рис. 4.12) к статору из сети подводится мощность

Часть этой мощности затрачивается на покрытие электрических потерь ΔРэл1 в активном сопротивлении обмотки статора и магнитных потерь ΔРм1 в статоре. В ротор посредством вращающегося магнитного поля передается электромагнитная мощность

Часть электромагнитной мощности, полученной ротором, тратится на покрытие электрических потерь ΔРэл2 в его обмотке. В машинах с фазным ротором возникают также потери в щеточных контактах на кольцах, которые обычно включают в потери ΔРэл2. Оставшаяся часть мощности Рэм превращается в механическую мощность

Магнитные потери ΔРм2 в стали ротора из-за малой частоты перемагничивания практически отсутствуют. Механическая мощность, за исключением небольших потерь на трение, является выходной полезной мощностью двигателя:

где ΔРт и ΔРдоб — соответственно потери на трение (механи-ческие) и добавочные потери.

Выразим электромагнитную и механическую мощности через электромагнитный вращающий момент М:

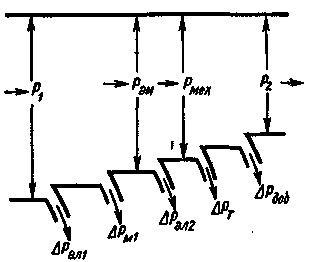Рис. 4.12. Энергетическая диаграмма асинхронной машины

где ω1 = 2πn1 /60 и ω2 = 2πn2 /60 — угловые скорости магнитного поля и ротора.

Из энергетической диаграммы (рис. 4.12) следует, что

или

Из формулы (4.20) имеем

Формулы (4.21) и (4.22) позволяют произвести анализ важнейших свойств асинхронного двигателя, а именно - установить связь между скольжением и КПД, а также зависимость электромагнитного момента от параметров машины и режима ее работы.

Связь между скольжением и КПД. Представим КПД асинхронного двигателя в виде

где η1 и η2 — КПД статора и ротора.

Поскольку

справедливо неравенство

Следовательно, η < η2 < (1 — s).

Таким образом, для работы асинхронного двигателя в номинальном режиме с высоким КПД необходимо, чтобы в этом режиме он имел небольшое скольжение. Обычно sном = 0,01 ÷ 0,06, при этом обмотку ротора выполняют с He6oльшим активным сопротивлением.

Номинальную частоту вращения ротора

можно принять равной приблизительно 0,97n1.

Значения частоты вращения n1 и приближенные значения n2 для асинхронных двигателей общепромышленного применения при f1 = 50 Гц в зависимости от числа полюсов 2р приведены ниже:

Незначительное отклонение частоты вращения ротора от синхронной частоты вращения магнитного поля позволяет в технических документах указывать не величину n2ном, а величину n1 или число полюсов.

Электромагнитный момент. Формулу (4.21), полученную из энергетической диаграммы, преобразуем к более удобному для анализа виду, подставив в нее значения

где ψ2 —угол сдвига фаз между ЭДС и током ротора.

При этом с учетом (4.13) получаем

где сM = рm2 kоб2 /√2 - постоянная.

Формула (4.29) справедлива не только для асинхронных машин, но и для электрических машин всех типов. Во всех этих машинах электромагнитный момент пропорционален произведению магнитного потока на активную составляющую тока ротора.

Поясним физический смысл этой формулы на примере асинхронного двигателя с короткозамкнутым ротором. На рис. 4.13 изображена развертка ротора, где кружками показаны поперечные сечения стержней. Вращающийся магнитный поток (кривая индукции в воздушном зазоре Bδ), пересекая проводники обмотки ротора, индуцирует в них переменную синусоидальную ЭДС, мгновенное значение которой е = Bδ lv. Следовательно, кривая распределения индукции Bδ вдоль окружности ротора представляет собой кривую распределения мгновенных значений ЭДС в стержнях, выраженную в другом масштабе. Направление этих ЭДС, определенное по правилу правой руки, показано крестиками и точками ниже сечений стержней. Мгновенное значение тока i в стержнях также изображается синусоидой (кривая i), сдвинутой относительно кривой ЭДС на угол ψ2. Направление тока в них отмечено крестиками и точками, проставленными внутри стержней.

Ток ротора, взаимодействуя с магнитным потоком, вызывает появление электромагнитных сил. При этом на каждый проводник действует усилие f = Bδ li. Распределение усилий по стержням представлено кривой f. Таким образом, к проводникам, лежащим на дуге π - ψ2, приложены силы, увлекающие ротор за вращающимся магнитным потоком,

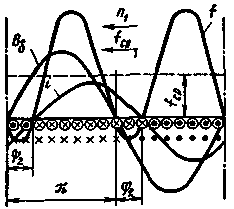Рис. 4.13. Кривые распределения индукции, тока и электромагнитных сил, действующих на проводники асинхронной машины

а на дуге ψ2 — тормозящие силы. Поэтому при неизменной силе тока I2 результирующее усилие Fрез, а следовательно, и вращающий момент М тем меньше, чем больше угол ψ2. В пределе при ψ2 = π/2 момент М = 0, так как на половину проводников действует усилие, направленное в одну сторону, а на другую половину - такое же усилие, направленное в противоположную сторону.

Формула (4.29) позволяет установить связь между значением момента и физическими явлениями, происходящими в двигателе. Ею удобно пользоваться при качественном анализе поведения двигателя в различных режимах. Недостаток формулы (4.29) заключается в том, что входящие в нее величины (Фm , I2 и cosψ2 ) не связаны непосредственно с напряжением сети и режимом работы машины, а их экспериментальное определение довольно сложно. Поэтому ниже выведена другая формула для электромагнитного вращающего момента, позволяющая более просто определять его значение и влияние на него различных параметров машины в эксплуатационных режимах.