§ 4.14. РАБОТА АСИНХРОННОГО ДВИГАТЕЛЯ ПРИ НЕСИНУСОИДАЛЬНОМ НАПРЯЖЕНИИ

В схемах частотного регулирования, когда асинхронный двигатель получает питание от статического преобразователя частоты, к обмоткам двигателя подводится несинусоидальное напряжение прямоугольной формы (см. рис. 4.45, б). Анализ особенностей работы асинхронного двигателя от несинусоидального напряжения обычно проводят, разлагая заданную форму кривой напряжения в гармонический ряд и исследуя отдельно действие каждой гармонической. При указанной форме подведенного к фазе напряжения гармонический ряд не содержит четных гармонических:

Высшие гармонические питающего напряжения обусловливают появление высших гармонических тока и магнитного потока, вследствие чего возникают дополнительные потери в обмотках и стали магнитопровода. Кроме того, наличие высших гармонических приводит к появлению вращающих и тормо­зящих моментов от взаимодействия токов и потоков одного порядка, а также колебательных моментов от взаимодействия между собой гармонических разных порядков.

Магнитное поле. Каждая гармоническая напряжения создает магнитное поле, вращающееся с частотой

Исключение составляют третья гармоническая и другие, кратные трем, которые создают пульсирующее поле, так как МДС указанных гармонических во всех трех обмотках статора совпадают по времени. Если преобразователь частоты обеспечивает сдвиг по фазе между первыми гармоническими напряжения трех фаз α1 = 120°, то для высших гармонических этот сдвиг αv = 120°v. Однако для третьей гармонической α3 = 360°, что равносильно отсутствию сдвига по фазе. Различие в сдвигах по фазе приводит к тому, что направления вращения магнитных полей, созданных высшими гармоническими тока, различны, так как у них различно чередование максимума токов в фазах. Например, для пятой гармонической α5 = 120° • 5 = 600° = 2 • 360° — 120°, т. е. чередование максимумов тока в фазах является обратным по сравнению с чередованием токов первой гармонической. Следовательно, пятая гармоническая магнитного потока вращается в сторону, противоположную направлению вращения основного магнитного поля (поля первой гармонической). Для седьмой гармонической α7 = 120° • 7 = 840° = 2 • 360° + 120° чередование максимумов тока, а следовательно, и направление вращения поля совпадают с первой гармонической.

В табл. 4.1 приведены данные для магнитных полей высших гармоник, вычисленные до 25-й гармоники включительно.

Номер гармонической	Амплитуда	Направление вращения	Скольжение Sv при S1 = 0	Номер гармонической	Амплитуда	Направление вращения	Скольжение Sv при S1 = 0
1	1	+	0	15	0.066	0	-
3	0.333	0	-	17	0.059	-	1.06
5	0.200	-	1.2	19	0.052	+	0.95
7	0.143	+	0.86	21	0.047	0	-
9	0.111	0	-	23	0.043	-	1.04
11	0.091	-	1.09	25	0.040	+	0.96
13	0.077	+	0.92

Знаком « + » показано совпадение направления вращения поля высшей гармонической с первой, знаком «-» - обратное направление вращения, знаком «0» — неподвижное поле (для третьей гармонической и гармонических, кратных трем).

Наиболее опасной является третья гармоническая напряжения, так как она имеет максимальную амплитуду и сравнительно небольшую частоту. Поэтому во всех устройствах частотного регулирования необходимо устранение третьей гармонической тока путем применения специальных реакто­ров или соединения обмоток двигателя по схеме Y, что исключает прохождение совпадающих во времени третьих гармонических тока.

Схема замещения. Расчет действия высших гармонических (с 5-й и выше, кроме кратных трем) целесообразно проводить по схеме замещения асинхронного двигателя (рис. 4.52). Скольже­ние для высших гармонических можно определить по формуле

Поскольку при номинальном режиме работы скольжение для первой гармонической невелико (s1ном = 0,02÷0,05), приближенное значение sv (при s1 =0):

Очевидно, что знак « + » в формуле (4.78 а) соответствует отрицательному направлению поля высшей гармонической. Значения sv, подсчитанные по формуле (4.78 а), приведены в табл. 4.2. Данные таблицы показывают, что в первом приближении скольжение для высших гармонических может быть принято равным единице. Индуктивные сопротивления Xvl и X'v2, обусловленные потоками рассеяния, пропорциональны частоте и берутся кратными номеру гармонической

Активные сопротивления в машинах небольшой мощности не зависят от частоты:

Как показывает практика, в машинах средней и большой мощности при высоких частотах происходит довольно интенсивное вытеснение тока, вследствие чего активные сопротивления увеличиваются с возрастанием частоты и их можно определять по формулам, аналогичным для индуктивных сопротивлений:

При расчетах высших гармонических токов намагничивающим контуром схемы замещения можно пренебречь в связи с малостью амплитуд напряжений и повышенной частотой. Поэтому ток в рабочем контуре схемы замещения для машин средней и большой мощности

Электрические потери в обмотках от токов высших гармонических. Эти потери определяются по схеме замещения (рис. 4.52). Для крупных электрических машин

ΔPэлv = m1 Iv2(Rv1 + R'v2 ) =

m1 Uv2(Rv1 + R'v2 ) (Rv1 + R'v2 )2 + (Xv1 + X'v2 )2

=

=

m1 U12v(R1 + R'2 )/v2 v2[(R1 + R'2 )2 + (X1 + X'2 )2]

=

m1 U12(R1 + R'2 ) v3[(R1 + R'2 )2 + (X1 + X'2 )2]

=

Pк v3

где Рк = m1U12(R1 + R'2)/[(R1 + R'2)2 + (X1+X'2)2] - электрические потери в обмотках двигателя в режиме короткого замыкания при номинальном синусоидальном напряжении. Электрические потери в обмотках двигателя при коротком замыкании Рк больше электрических потерь ΔРэл.ном при номинальном режиме и номинальном синусоидальном напряжении: где kп = (Iп /Iном ) — отношение пускового тока к номинальному; для машин, работающих при синусоидальном напряжении, kп = 5÷7, а для машин, работающих при прямоугольном напряжении, kп = 3÷5.

Поэтому

Коэффициент увеличения электрических потерь в двигателе при питании его напряжением прямоугольной формы

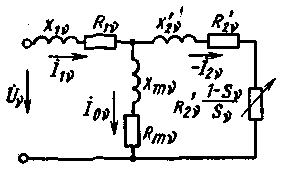Рис. 4.52. Упрощенная схема замещения   асинхронного   двигателя при питании его  несинусоидальным напряжением

При kп = 3÷5 этот коэффициент

Следовательно, в крупных машинах увеличение электрических потерь может быть довольно существенном и примерно равноценным возрастанию тока на 5 — 15%. Чтобы уменьшить электрические потери, крупные машины, работающие при несинусоидальном напряжении, обычно выполняют на пониженную кратность пускового тока kп = 3÷5, т. е. с увеличенными значениями индуктивных сопротивлений X1 и X2 . Это, в свою очередь, приводит к снижению перегрузочной способности двигателя. В машинах небольшой мощности электрические потери в обмотках возрастают в меньшей степени так как у них активное сопротивление из-за вытеснения тока увеличивается незначительно. Аналогично предыдущему для них

Магнитные потери в стали от высших гармонических. Обычно магнитные потери невелики, так как амплитуды высших гармонических магнитного потока малы. Поскольку для высших гармонических машина находится в режиме короткого замыкания, приближенно можно принять, что ЭДС статора Ev ≈ 0,5 Uv. Относительное значение потока

При прямоугольной форме напряжения

В первом приближении магнитные потери в стали можно определить по соотношению

Магнитные потери в стали от пятой гармонической составляют около 0,5% от основных потерь, от седьмой гармонической — 0,19 % и т. п. Суммарные потери в стали от высших гармонических, определенные по формуле (4.85), не превышают 0,7%. Формула (4.85) не является точной, так как магнитные потери ΔPмv от высших гармонических возникают из-за перемагничивания стали по частичному циклу и имеют примерно в два раза большую величину, чем по формуле; однако это не изменяет вывода о незначительном увеличении потерь в стали.

Вращающие и тормозящие моменты от высших гармонических. Эти моменты рассчитывают так же, как электромагнит­ный момент от основной гармонической:

или где ωv — угловая скорость магнитного поля данной гармони-ческой; sv — скольжение для поля данной гармонической.

Направление момента определяется направлением вращения поля высшей гармонической относительно основного поля — при совпадении направлений этих полей момент вращающий, при несовпадении — тормозной. Из табл. 4.1 видно, что вращающим моментам соответствует s < l ; тормозным — s > 1 .

Для упрощенной оценки моментов можно положить электрические потери в роторе равными потерям в статоре:

Считая, как и прежде, для высших гармонических sv ≈ 1 и ωv ≈ ω1v, получаем

где Мп ≈ 0,5Pк /ω1 — пусковой момент от основной гармонической напряжения при тех же условиях (электрические потери в роторе и в статоре одинаковы).

Обычно пусковой момент двигателей с короткозамкнутым ротором Мп ≈ Мном . Следовательно, моменты от высших гармонических весьма незначительны, например от пятой гармонической момент Мv менее 0,2% от Мп и т. п.:

Номер гармонической.	1	5	7	11	13	17
Мv /Мп	+ 1	-1.6*10-3	+0.4*10-3	-0.07*10-3	+0.035*10-3	-0.012*10-3

В малых машинах, где эффект от вытеснения тока невелик, моменты еще меньше:

т. е. меньшим машинам соответствуют меньшие значения Mv /Mп.

Колебательные моменты. В результате взаимодействия токов одних частот с потоками других возникают знакопеременные моменты, частота которых значительно выше основной частоты, а среднее значение равно нулю. Общее количество колебательных моментов очень велико, так как взаимодействие возникает между всеми гармоническими. Однако колебательные моменты, возникающие от взаимодействия высших гармонических между собой, имеют тот же порядок, что и рассмотренные выше вращающие моменты, т. е. пренебрежимо малы. Практически могут иметь значение лишь колебательные мо­менты, образуемые взаимодействием высших гармонических тока ротора с магнитным потоком основной гармонической. Мгновенное значение такого колебательного момента

Знаки «+», «—» в скобках аргумента зависят от того, совпадает направление вращения волны МДС высшей гармонической с направлением вращения основной гармонической или нет. Например, пятая гармоническая МДС имеет отрицательное направление (см. табл. 4.2); следовательно, частота ее относительно МДС первой гармонической: n5,1 = n1 - ( - n5 ) = n1 - (-5n1) = 6n1 . Для седьмой гармонической оба направления вращения совпадают: n7,1 = n1 - n7 = n1 - 7n1 = - 6n1 . Таким образом, колебательные моменты, создаваемые парой соседних гармонических тока ротора с первой гармонической потока, имеют одну и ту же частоту (в данном случае 6n1), но противоположны по знаку.

Обычно достаточно бывает рассмотреть две пары колебательных моментов: моменты от пятой и седьмой гармонических и моменты от одиннадцатой и тринадцатой гармонических. Амплитудное значение колебательных моментов соответствующих пар

Поскольку момент от основной гармонической

получаем

Для крупных электрических машин согласно (4.81)

где Iк - ток короткого замыкания двигателя при синусоидальном питающем напряжении.

Полагая при номинальном режиме cos ψ21ном ≈ 1,0 и I21ном ≈ Iк /kп , получаем

Значения амплитуд колебательных моментов, вычисленные по формуле (4.94) при kп = 3÷5, составляют 7-12% от М1ном для момента, изменяющегося с частотой 6ω1 (от пятой и седьмой гармонических), и 0,8—1,5% для момента, изменяющегося с частотой 12ω1 (от одиннадцатой и тринадцатой гармонических).

Амплитуда колебательных моментов не Зависит от значения нагрузки. Поэтому при небольшой нагрузке в режиме, близком к холостому ходу, амплитуда колебательных моментов может превышать основной электромагнитный момент двигателя. Это явление может вызвать неравномерность вращения ротора, особенно заметное при малых частотах, когда периоды изменения колебательного момента достаточно велики.