§ 3.8. РАССЕЯНИЕ И ИНДУКТИВНЫЕ СОПРОТИВЛЕНИЯ ОБМОТОК В МАШИНАХ ПЕРЕМЕННОГО ТОКА

Магнитные проводимости потоков рассеяния. В машинах переменного тока потоки рассеяния и соответствующие им индуктивные сопротивления имеют относительно большие значения по сравнению с трансформаторами. Это объясняется тем, что в машинах проводники обмоток располагают в пазах, и, следовательно, длина путей потоков рассеяния по воздуху сокращается.

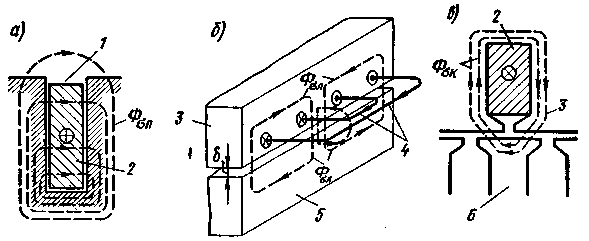
В общем случае в машине имеются следующие потоки рассеяния: пазовый Фσп, проходящий через стенки паза (рис. 3.36, а); лобовой Фσл, замыкающийся вокруг лобовых частей обмотки (рис. 3.36,6); поток Фσк, замыкающийся через головки (коронки) зубцов и воздушный зазор, но сцепленный только с одной из обмоток (рис. 3.36, в); дифференциальный Фσд, обусловленный наличием высших гармонических в кривой поля и ЭДС. Каждому потоку соответствует определенная магнитная проводимость, поэтому магнитную проводимость для потоков рассеяния обычно представляют в виде

где Λп, Λл, Λк, Λд — соответственно проводимости потоков Фσп, Фσл, Фσк и Фσд. При нахождении потоков рассеяния и создаваемых ими индуктивных сопротивлений обычно используют удельные магнитные проводимости (на единицу расчетной активной длины li машины), так как они определяются геометрическими размерами тех частей машины, через которые проходит соответствующий поток рассеяния. При этом

Рис.   3.36.   Силовые  линии   потоков   рассеяния  в   электрических машинах переменного тока: 1— паз;  2 — проводник;  3 — статор;  4 — лобовые  части;  5 —ротор;  б — зубец ротора

За расчетную активную длину li при определении потоков рассеяния принимают конструктивную длину l соответствую-щей части машины (статора или ротора); при наличии в ней пк радиальных вентиляционных каналов шириной bк

Пазовый поток рассеяния. На рис. 3.37 изображена обмотка переменного тока, проводники которой на двух полюсных делениях 2τ распределены в шести пазах, т. е. при q = 3. Вокруг проводников с током показан поток рассеяния Фσп, построенный обычным способом исходя из равномерного распределения МДС. Поток рассеяния, образуемый проводниками рассматриваемой обмотки, согласно закону полного тока

где qFп — суммарная МДС обмотки; Fп — МДС проводников, расположенных в одном пазу; Rм.п — магнитное сопротивление для потока рассеяния, соответствующее одному пазу.

Таким образом, пазовый поток рассеяния Фσп, сцепленный с проводниками одного паза, можно рассматривать как поток уединенного паза и считать, что проводники, расположенные в соседних пазах, не влияют на этот поток.

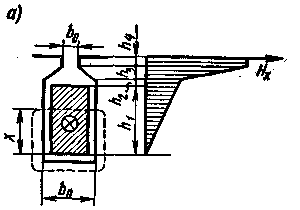
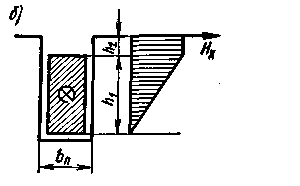
Для определения проводимости Λп потока рассеяния, проходящего через стенки паза, и соответствующего ему индуктивного сопротивления рассмотрим распределение напряженности Нх этого потока вдоль высоты паза (рис. 3.38). МДС для изображенного на рис. 3.38, а штриховой линией контура обхода (на расстоянии х от нижнего края проводников)

где Fп =√2Iф wп — МДС, расположенной в пазу катушки, по которой проходит ток фазы Iф ; wп — число витков катушки; h1 — высота проводников с током.

Если пренебречь магнитным напряжением на стальных участках рассматриваемого контура, то напряженность магнитного поля в части паза высотой h1 где расположены проводники с током, Нх = (Fп /bп )(x/h1 ).

Рис. 3.37. Схема образования потоков рассеяния вокруг проводников, расположенных в пазах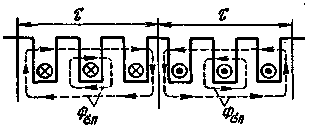

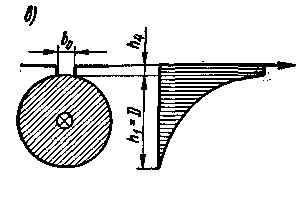	Рис. 3.38. Распределение напряженности потока рассеяния вдоль высоты паза для полузакрытого, открытого и круглого пазов

МДС Fx в части паза, расположенной выше проводников с током, остается постоянной, а напряженность поля Нх изменяется обратно пропорционально расстоянию между стенками паза в рассматриваемом сечении. Следовательно, потокосцепления потока рассеяния Фσп с расположенной в пазу катушкой на различных участках паза равны: на участке высотой h1

на участке высотой h2 на участке высотой h3

Ψ3 = μ0 Fп li

h1 ∫ 0

dx bп - x h3 (bп - b0)

= μ0 Fп wп li

h3 b3

,

где b3 - (bп - b0 )/[ln(bп /b0 )] ≈ (bп + b0 )/2,3; на участке высотой h4

Общее потокосцепление катушки, расположенной в пазу,

где коэффициент «2» указывает на потокосцепление второй стороны катушки.

При этом индуктивность катушки, обусловленная пазовым потоком рассеяния,

а магнитная проводимость потока где удельная проводимость

В одной фазе однослойной обмотки содержится pq пазовых катушек, которые в общем случае образуют а параллельных ветвей. Поэтому индуктивность фазы обмотки, обусловленная проводимостью пазового потока рассеяния,

Учитывая, что общее число последовательно включенных витков в фазе wф = wп pq/a, получаем, что

Таким образом, составляющая индуктивного сопротивления фазы, обусловленная пазовыми потоками рассеяния,

При других конфигурациях пазов удельная проводимость λп определяется аналогично. При открытых пазах (рис. 3.38,6) оба последних члена в уравнении (3.47) исчезают. При круглых пазах (рис. 3.38, в)

т. е. диаметр находящегося в пазу проводника не влияет на поток рассеяния, так как одновременно пропорционально изменяются ширина и высота паза.

Полученные формулы справедливы для однослойных обмоток. В двухслойных обмотках при шаге обмотки у ≠ τ в некоторых пазах проводники верхнего и нижнего слоев принадлежат к различным фазам и токи в них сдвинуты между собой по фазе. Это изменяет магнитное поле паза, вследствие чего проводимость пазового потока уменьшается. Поэтому для двухслойной обмотки

где ks = (1 + 3β)/4 — коэффициент, равный единице при диаметральной обмотке, т. е. при у = τ, и меньше единицы при укороченном шаге, когда у < τ и β = y/τ < 1.

Поток рассеяния вокруг лобовых частей катушек. Вокруг лобовых частей катушек замыкается поток, часть которого является потоком взаимоиндукции, а другая часть — потоком рассеяния. Поток рассеяния определяется геометрическими размерами и типом обмотки. На рис. 3.39 для примера показана картина магнитного поля от потоков рассеяния Фσл вокруг лобовых соединений для однослойной обмотки.

Удельная проводимость потока рассеяния

где с - постоянный коэффициент, равный 0,67 для однослойных двухплоскостных обмоток; 0,47 - для трехплоскостных; 0,34 - для двухслойных обмоток; lл - средняя длина лобовых частей.

Формула (3.52) является эмпирической, так как аналитическое определение проводимости приводит к весьма сложным и громоздким выражениям. Подобные формулы для определения удельной проводимости λл для короткозамкнутых и других специальных обмоток приводятся в пособиях по проектированию электрических машин.

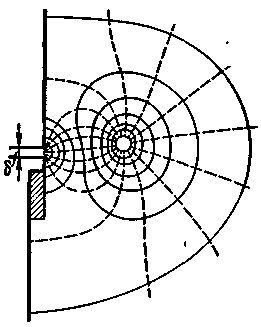Рис.  3.39.  Магнитное  поле  от потоков рассеяния вокруг лобовых   соединений    однослойной обмотки

Рис.   3.40.   Схема  прохождения потока рассеяния через головки зубцов.

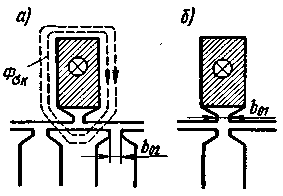Поток  рассеяния  по  головкам  (коронкам)  зубцов.   Поток рассеяния Фσк, проходящий через головку каждого зубца, зависит от взаимного положения зубцов ротора и статора. Когда середина рассматриваемого паза, например статора, находится против середины зубца ротора, поток рассеяния статора Фσк максимален (рис. 3.40, а). При повороте ротора этот поток постепенно уменьшается и становится равным нулю, когда середина паза ротора окажется против середины паза статора (рис. 3.40,6). Но статор и ротор имеют обычно различные числа пазов, вследствие чего отдельные пазы, принадлежащие одной фазе обмотки статора (или ротора), занимают различное положение относительно головок зубцов ротора (статора). В результате потокосцепления всей фазной обмотки, обусловленные проводимостью через головки зубцов, мало зависят от взаимного положения ротора и статора.

Приближенно средняя удельная проводимость по головкам Зубцов

где n1 = (t1 - b01 - b02)/2 (b01 и b02 - ширина прорезей в пазах статора и ротора); t1 - зубцовое деление; δ - воздушный зазор.

Проводимость по головкам зубцов тем больше, чем больше зубцовое деление и меньше воздушный зазор между статором в ротором.

Дифференциальное рассеяние. Распределение обмотки по пазам приводит к тому, что ее МДС изменяется ступенчато. Вследствие этого в кривой распределения индукции вдоль окружности статора и ротора имеются пространственные высшие гармонические. Например, фаза АХ создает пространственные высшие гармонические

Взаимодействуя с другими фазами, высшие гармонические, так же как и первая гармоническая, создают вращающиеся магнитные поля, которые индуцируют в обмотках соответствующие ЭДС. Поскольку высшие гармонические токов не могут передавать мощность из одной обмотки в другую, создаваемые ими магнитные потоки относят к потокам рассеяния, которым соответствует некоторая удельная проводи-мость λд, называемая дифференциальной.

Амплитуды высших гармонических магнитных потоков тем меньше, чем меньше зубцовые деления, и зависимость их от числа пазов сходна с аналогичной зависимостью проводимости по головкам зубцов от числа пазов. По этой аналогии очень часто определяют расчетную дифференциальную проводимость λ'д, учитывающую наличие как высших гармонических потоков, так и рассеяние через головки зубцов. При этом λ'д = λд + λк.

Наиболее часто употребляют эмпирическую формулу

где t - зубцовое деление статора или ротора, kδ - коэффициент воздушного зазора, учитьвающий наличие пазов на статоре и роторе; ξ — коэффициент, значение которого зависит от величины q, укорочения шага обмотки β и геометрических размеров воздушного зазора и зубцовой зоны (отношение b0/t и b0/δ).

Индуктивное сопротивление рассеяния обмотки, обусловленное всеми потоками рассеяния, по аналогии с (3.49) можно выразить формулой

где λ = λп + λл + λ'д.