Глава десятая
АСИНХРОННЫЕ МАШИНЫ
10.12. МЕХАНИЧЕСКАЯ ХАРАКТЕРИСТИКА АСИНХРОННОГО ДВИГАТЕЛЯ
Механической характеристикой называется зависимость частоты вращения ротора двигателя или скольжения от момента, развиваемого двигателем при установившемся режиме работы.
n= f(М) или s = f(M).
Механическая характеристика является одной из важнейших характеристик двигателя. При выборе двигателя к производственному механизму из множества двигателей с различными механическими характеристиками выбирают тот, механическая характеристика которого удовлетворяет требованиям механизма.
Уравнение механической характеристики асинхронного двигателя может быть получено на основании формулы (10.41) и схемы замещения.
С помощью схемы замещения (см. рис. 10.17) определяют приведенный ток фазы ротора:
| I'2 = | U1ф | , | |||
| √ | (r1 + | r'2 | ) + (x1 + x'2)2 | ||
| s | |||||
| r'2 | = r'2 + | r'2(1 - s) | . |
| s | s |
Полученное значение тока I'2 nподставляют в уравнение момента (10.41), в котором предварительно I2 и r2 заменяют через их приведенные значения:
| M = | 3I22r2 | = | 3I'22r'2 | . |
| ω0s | ω0s |
| M = | 3U1ф2r'2 | = | ||
| ω0s [(r1 + | r' | )2 + (x1 + x'2)2] | ||
| s | ||||
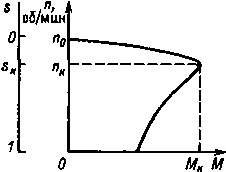 |
| Рис. 10.18. Механическая характеристика асинхронного двигателя |
Выражение (10.51) представляет собой уравнение механической характеристики, поскольку оно связывает момент и скольжение двигателя. Остальные входящие в уравнение величины: напряжение сети и параметры двигателя — постоянны 1 и не зависят от s и М. Располагая параметрами двигателя, можно рассчитать и построить его механическую характеристику, которая будет иметь вид, изображенный на рис. 10.18.
1 Сопротивление r2 зависит от частоты f2 и, следовательно, от s, но для двигателей общего назначения изменение r2 незначительно.
Однако необходимо отметить, что после включения двигателя в нем происходят сложные переходные электромагнитные процессы. В тех случаях, когда время разбега оказывается соизмеримым с временем электромагнитных процессов, механическая характеристика двигателя в период разбега может существенно отличаться от статической.
Одной из важных точек характеристики, представляющей интерес при анализе работы и выборе двигателя, является точка, где момент, развиваемый двигателем, достигает наибольшего значения. Эта точка имеет координаты nкр , sкр , Mmax . Значение критического скольжения sкр , при котором двигатель развивает максимальный (критический) момент Мmax, легко определить, если взять производную dM/ds выражения (10.51) и приравнять ее нулю.
После дифференцирования и последующих преобразований выражение sкр будет иметь следующий вид:
| sкр = ± | r'2 | . |
| √r12 + xк2 |
Подставив sкр вместо s в уравнение (10.51), получим выражение максимального момента
| Мmax = | 3U1ф2 | . |
| 2ω0(r1 ± √r12 + xк2) |
Необходимо отметить, что из выражений (10.51) — (10.53) вытекает следующее.
Момент, развиваемый двигателем, при любом скольжении пропорционален квадрату напряжения. Максимальный момент пропорционален квадрату напряжения и не зависит от сопротивления цепи ротора. Критическое скольжение пропорционально сопротивлению цепи ротора и не зависит от напряжения сети.
Полученные выражения удобны для анализа, однако из-за отсутствия в каталогах параметров r1, х1, х2 их использование для расчетов и построения характеристик затруднено.
В практике обычно пользуются уравнением механической характеристики, с помощью которого можно произвести необходимые расчеты и построения, используя только каталожные данные.
Активное сопротивление обмотки статора r1 значительно меньше остальных сопротивлений цепи статора и ротора, и им обычно пренебрегают. Тогда выражения (10.51) — (10.53) будут иметь вид
| M = | 3U1ф2r'2 | ; |
| ω0s [(r'2/s)2 + хк2] |
sкр = ± r'2/хк;
| Mmax= | 3U1ф2 | ; |
| 2ω0хк |
Упрощенное уравнение механической характеристики получается из совместного решения уравнений (10.54) — (10.56):
| M = | 2M max | ; |
| s/sк + sк/s |
Значение Мmax определяется из отношения Мmax/Мном = λ, указываемого в каталогах, a sкр — из уравнения (10.57), если решить его относительно sкр и вместо текущих значений s и М подставить их номинальные значения, которые легко определить по паспортным данным:
sкр = sном (λ ± √λ2 - 1),
Следует отметить, что в зоне от М = 0 до М ≈ 0,9Мmax механическая характеристика близка к прямой линии. Поэтому, например, при расчетах пусковых и регулировочных резисторов эту часть механической характеристики принимают за прямую линию, проходящую через точки М = 0, n = n0 и Мном , nном . Уравнение механической характеристики в этой части будет иметь вид
| M = | Мном | s. |
| sном |
