ЭЛЕКТРОТЕХНИКА

Глава третья
ТРЕХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

3.5. СОЕДИНЕНИЕ ПРИЕМНИКОВ ТРЕУГОЛЬНИКОМ

Как видно из схемы рис. 3.12, каждая фаза приемника при соединении треугольником подключена к двум линейным проводам. Поэтому независимо от значения и характера сопротивлений приемника каждое фазное напряжение равно соответствующему линейному напряжению:

Если не учитывать сопротивлений проводов сети, то напряжения приемника следует считать равными линейным напряжениям источника.

На основании схемы рис. 3.12 и выражения (3.16) можно сделать вывод о том, что соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника или однофазные приемники рассчитаны на напряжение, равное номинальному линейному напряжению сети.

Фазные токи Iab , Ibc и Iса в общем случае не равны линейным токам Ia , Ib и Ic . Применяя первый закон Кирхгофа к узловым точкам а , b и с, можно получить следующие соотношения между линейными и фазными точками:

Используя указанные соотношения и имея векторы фазных токов, нетрудно построить векторы линейных токов.

3.5.1. Симметричная нагрузка. В отношении любой фазы справедливы все формулы, полученные ранее для однофазных цепей, например

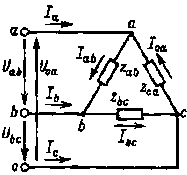Рис.   3.12.   Соединение   фаз приемника треугольником

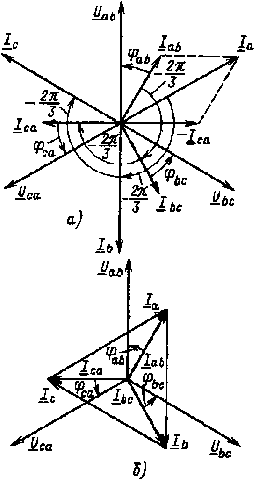Рис.   3.13.   Векторные   диаграммы   при   соединении   приемника   треугольником в случае симметричной нагрузки

Очевидно, при симметричной нагрузке

Векторная диаграмма фазных (линейных) напряжений, а также фазных токов при симметричной активно-индуктивной нагрузке приведена на рис. 3.13, а. Там же в соответствии с выражениями (3.17) построены векторы линейных токов. Следует обратить внимание на то, что при изображении векторных диаграмм в случае соединения треугольником вектор линейного напряжения Uab принято направлять вертикально вверх.

Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке существуют симметричные системы фазных и линейных токов.

Векторы линейных токов чаще изображают соединяющими векторы соответствующих фазных токов, как показано на рис. 3.13, б. На основании векторной диаграммы рис. 3.13, б

Ia = 2Iab sin 60° = √3Iab,
Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно   написать,   что   при   симметричной   нагрузке   вообще

Для определения мощностей трехфазного приемника при симметричной нагрузке можно воспользоваться полученными ранее формулами (3.13) и (3.14).

Пример 3.3. К трехфазной сети с линейными напряжениями Uл = 220 В должен быть подключен трехфазный приемник, каждая фаза которого рассчитана на напряжение 220 В и содержит активное сопротивление rф = 8,65 Ом, а также индуктивное сопротивление xф = 5 Ом, соединенные последовательно.

Определить фазные и линейные токи, углы сдвига фаз между фазными напряжениями и токами, а также мощности.

Решение. Так как каждая из фаз приемника рассчитана на напряжение, равное линейному напряжению трехфазной сети, фазы приемника должны быть соединены треугольником (см. рис. 3.12).

Полные сопротивления фаз, фазные и линейные токи:

Углы сдвига фаз между напряжениями и токами

Полная активная и реактивная мощности приемника и любой фазы

Векторные диаграммы приемника приведены на рис. 3.13.

3.5.2. Несимметричная нагрузка. Как и при соединении звездой, в случае соединения треугольником однофазные приемники делят на три примерно равные в отношении мощности группы. Каждая группа подключается к двум проводам, между которыми имеется напряжение, отличающееся по фазе от двух других напряжений сети (рис. 3.14). В пределах каждой группы приемники соединяются параллельно.

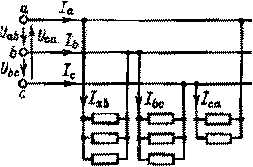Рис. 3.14. К вопросу о соединении однофазных приемников треугольником

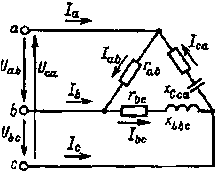Рис. 3.15. Схема цепи к примеру 3.4

После замены приемников каждой фазы одним приемником с эквивалентным сопротивлением и соответствующего их расположения получим схему, приведенную на рис. 3.12.

Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также фазные мощности можно определить по формулам (3.18). При несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными. Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bс — активно-индуктивная, а в фазе са — активно-емкостная (рис. 3.15), приведена на рис. 3.16. Построение векторов линейных токов произведено в соответствии с выражениями (3.17).

Для определения мощностей всех фаз следует пользоваться формулами

Формулы (3.13) и (3.14), полученные ранее для симметричной нагрузки, не пригодны для определения мощностей при несимметричной нагрузке.

Если кроме фазных токов требуется определить линейные токи, задачу следует решать в комплексной форме. Для этой же цели можно воспользоваться векторной диаграммой.

При решении задачи в комплексной форме необходимо прежде всего выразить в комплексной форме фазные напряжения, а также полные сопротивления фаз. Когда это сделано, нетрудно по закону Ома определить фазные токи. Например, комплексное выражение тока Iab будет

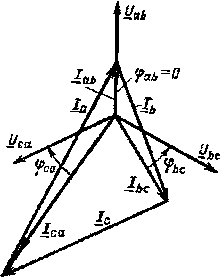Рис. 3.16. Векторная диаграмма фазных и линейных напряжений и токов при соединении приемника треугольником в случае несимметричной нагрузки

Линейные токи определяются через фазные с помощью выражений (3.17).

Комплексным методом можно воспользоваться и для определения фазных мощностей. Так, мощности фазы аb будут равны

Рассмотрим, как будут изменяться значения различных величин в электрической цепи рис. 3.15 при изменении сопротивления приемников. Например, если при xCca /rca = const увеличить вдвое сопротивление zca , то ток Ica уменьшится, а угол φca не изменится (см. рис. 3.16). Очевидно, при этом уменьшатся и токи Iа , Ic , а также мощности Рса , Qса , Sса . Токи Iаb , Ibc , Ib , углы φab , φbc , а также мощности Рab , Qab , Sab , Рbc , Qbc , Sbc останутся постоянными. При отключения фазы са сопротивление
zca = ∞, Iса = 0, токи Iаb , Ibc , Ib , а также углы φab , φbc не изменятся, а токи Iа и Ic уменьшатся Ia = Iab , Ic = - Ibc .

Пример 3.4, В электрической цепи рис. 3.15 Ua = 220 В, rаb = 40 Ом, rbc = 17,3 Ом, хLbc = 10 Ом, rса = 8,65 Ом,
хСса = 5 Ом. Определить фазные и линейные токи, а также мощности.

Решение. Условимся определять линейные токи аналитически, для чего будем решать задачу комплексным методом. Поскольку вектор линейного напряжения Uab при соединении в треугольник принято обычно направлять как вектор ЭДС Еа вертикально вверх (см. рис. 3.2, б), для определения комплексных значений линейных напряжений можно воспользоваться выражениями (3.2). Получим

Комплексные значения полных сопротивлений фаз

Комплексные и действующие значения фазных и линейных токов:

Iab =	Uab	=	220	= 5,5 А;   Ibc = - 9,5 - j5,5 А;
	Zab		40

Далее можно решать задачу, не прибегая к комплексному методу. Активные, реактивные и полные мощности фаз:

Рab = Iab2rab = 1210 Вт; Рbc = 2090 Вт; Рca = 4190 Вт; Qab = 0; Qbc = Ibc2xLbc = 1210 вар;
Qca = Ica2xCca = - 2420 вар; Sab = Рab = 1210 В•А; Sbc = Ubc Ibc = 2420 В•A; Sca = Uca Ica = 4840 В•А.

Общие активные и реактивные мощности:

Углы сдвига фаз между фазными напряжениями и токами

φab = 0, φab = arcsin	xLbc	= 30°,   φca = arcsin	xCca	= - 30°.
	zbc		zca

Векторная диаграмма приемника дана на рис. 3.16.