ЭЛЕКТРОТЕХНИКА

Глава пятая
ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ЭДС, ТОКИ И НАПРЯЖЕНИЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

5.5. АНАЛИЗ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ НЕСИНУСОИДАЛЬНОМ НАПРЯЖЕНИИ ИСТОЧНИКА ПИТАНИЯ

Известно, что к линейным электрическим цепям применим метод наложения. В соответствии с этим запись периодическо­го несинусоидального напряжения источника энергии рядом Фурье дает возможность представить его несколькими последовательно соединенными и одновременно действующими ис­точниками ЭДС или напряжений и осуществлять анализ электрического   состояния   цепей   на   основе   метода   наложения.

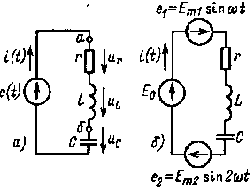Рис. 5.7. Электрическая цепь с источником несинусоидальной ЭДС (а) и ее схема замещения (б)

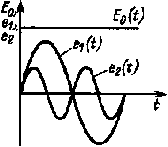Рис. 5.8. Временные диа­граммы ЭДС источников

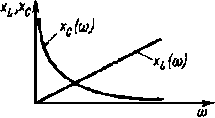Рис. 5.9. Частотные характеристики индуктивного и емкостного элементов

Например, рассмотрим электрическую цепь рис. 5.7, а, в которой к источнику с несинусоидальной ЭДС

подключены последовательно резистивный, индуктивный и емкостный элементы.

С учетом вышесказанного в рассматриваемой электрической цепи ЭДС e(t) может быть представлена тремя ЭДС (рис. 5.7, б). Графики E0(t), а также e1(t) и e2(t) изображены на рис. 5.8. В соответствии с методом наложения данная электрическая цепь рассчитывается как цепь, в которой действуют три независимые ЭДС. При этом определение тока и напряжений от ЭДС E0 осуществляется, как при расчете цепей постоянного тока, а от ЭДС e1 и е2 — как при расчете цепей синусоидального тока. При расчете цепи от ЭДС е2 и ЭДС более высших гармоник необходимо производить пересчет значений xL и хC, так как они зависят от частоты (рис. 5.9):

xLk = kωL;    хCk =	1	.
	kωС

В анализируемой электрической цепи постоянная составляющая ЭДС E0 не вызывает установившегося тока, так как сопротивление емкостного элемента при постоянном токе равно  бесконечности  (рис.   5.9).   Определяем  ток  и   напряжение в электрической цепи с ЭДС е1 и е2. Для первой гармоники

где

Ilm =	Elm	=	Elm	;    φ1 = arctg	ωL - 1/ωC	.
	z1		√r2 + (ωL - 1/ωC)2		r

В общем случае φk = ψke- ψki , тогда ψki = ψke - φk , а для первой гармоники ψ1i = ψ1e - φ1.

Для второй гармоники i2 = I2m sin (2ωt + φ2), где

I2m =	E2m	=	E2m	;
	z1		√r2 + (2ωL - 1/2ωC)2

φ2 = arctg	2ωL - 1/2ωC	;
	r

При этом ток цепи i = I0 + i1 + i2 и так как I0 = 0, то i = i1 + i2, т. е. i(t) = Ilm sin (ωt + ψ1) + I2m sin (2ωt + ψ2). Действующее значение тока цепи

I =	√	(	Ilm	)2 + (	I2m	)2.
			√2		√2

Напряжение ur резистивного элемента совпадает по фазе с током цепи и в общем случае

ur = U0r + u1r + u2r, а так как   U0r = I0r = 0, то ur = u1r + u2r , т. е.

где Ulmr = Ilmr; U2mr = I2mr.

Аналогично   могут   быть   определены   значения   uL и uC:

uC(t) = IlmxC sin(ωt + ψ1 - π/2) + I2m	xC	sin (2ωt + ψ2 - π/2).
	2

Определение гармонических составляющих токов i1 и i2, а также напряжений ur , uL и uС можно также осуществить с использованием комплексных чисел.

Пример 5.3. Несинусоидальная ЭДС e(t) линейной электрической цепи рис. 5.7, а изменяется по закону e(t) = 200 + 180 sin (ωt -- 30°) + 120 sin 3ωt. Параметры цепи: r = 6 Ом, xL = ωL = 2 Ом,
хC = 1/ωС = 18 Ом. Определить мгновенное, действующее значение тока в   цепи   и  действующее   значение   напряжения   на   участке   цепи   аb.

Решение. По отношению к постоянной составляющей ЭДС Е0 = 200 В сопротивление конденсатора равно бесконечности, т. е. хС = 1/ωС = 1/0•С = ∞. Следовательно, постоянная составляющая тока I0 =0.

Расчет первой гармоники:

полное сопротивление цепи

угол сдвига фаз между ЭДС е1  и током

φ1 = arctg	ωL - 1/ωС	= - 69°20';
	r

так как φ1 = ψ1e - ψ1i, то амплитуда и действующее значение первой гармоники тока

I1m =	E1m	=	180	= 10,5 A; I1 =	I1m	=	10,5	= 7,5 А;
	z1		17		√2		√2

мгновенное значение тока действующее значение напряжения на участке ab

Расчет для третьей гармоники:

полное сопротивление цепи

т. е. для данной гармоники наблюдается резонанс напряжений, а следовательно, угол сдвига фаз между ЭДС е3 и током

φ3 = arctg	3ωL - 1/3ωC	= 0;
	r

амплитуда и действующее значение тока

I3m =	E3m	=	120	= 20 A; I3 =	I3m	=	20	= 14,3 A.
	z3		6		√2		√2

мгновенное значение тока

i3 = 20 sin 3ωt;

действующее значение напряжения на участке ab

Uaб3 = I3zaб3= I3 √r2 + (3ωL)2 = 14,3 √62 + 62 = 121,3 В.

Расчет общего тока:

мгновенное значение тока в цепи

i(t) = 10,5 sin(ωt + 39°20') + 20sin 3ωt;

действующие значения тока в цепи и напряжения на участке аb

I = √I12 +I32 = √7,52 + 14,32 = 16,1 А;

Uaб = √U2aб1 + U2aб3 = √47,22 + 121,32 = 130,1 В.

В ряде случаев при проведении практических расчетов периодические несинусоидальные ЭДС и напряжения можно представить эквивалентными синусоидами: так, при изучении нелинейной электрической цепи, т. е. цепи, содержащей катушку с ферромагнитным магнитопроводом (см. гл. 6), несинусоидальный ток заменяется эквивалентной синусоидой. Подобная замена осуществляется так, чтобы действующее значение эквивалентной синусоиды ЭДС или напряжения равнялось действующему значению несинусоидальной величины.

При определении, например, действующего значения эквивалентной синусоиды напряжения Uэк путем обычного интегрирования по формуле, аналогичной (5.1), ее амплитудное значение

Uэкm = √2Uэк .

Мгновенное значение эквивалентной синусоиды напряжения

uэк = Uэкm sin ωt,

где ω = 2π/Т.

Расчет цепи ведется так же, как и цепей синусоидального тока, т. е. ток в цепи

Iэк = Uэк /Z.

Активная мощность цепи.

Р = Uэк Iэк cos φэк,

где cos φэк = r/z.