Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.7. ПОДКЛЮЧЕНИЕ ЦЕПИ С ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫМИ РЕЗИСТИВНЫМ r И ЕМКОСТНЫМ С ЭЛЕМЕНТАМИ К СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ
Допустим, что до включения цепи конденсатор был не заряжен. После замыкания выключателя (рис. 4.7, а) конденсатор начнет заряжаться, в результате в проводах возникнет ток и между обкладками конденсатора появится напряжение uC. Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид
0 = ir + uC - U.
Так как ток в цепи
i = dq/dt,
i = C duC/dt.
Подставив выражение тока i в (4.40), получим
Cr duC/dt + uC = U.
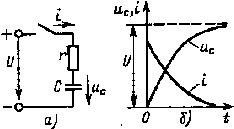 |
| Рис. 4.7 Зависимости i(t), uC(t)(б) при подключении цепи r, С (a) к сети с постоянным напряжением |
В этом случае, так же как и при анализе переходных процессов в цепях с индуктивностью, напряжение на емкости в переходный период состоит из двух слагаемых:
uC = uCуст + uCсв ,
Дифференциальное уравнение (4.41) без правой части
Cr duCсв /dt + uCсв = 0
uCсв = Aept.
Показатель степени р является корнем характеристического уравнения Сrр + 1 = 0:
| р = - | 1 | = - | 1 | . |
| rC | T |
Подставив в (4.43) р = - 1/Т, получим
uCсв = Ae-t/T.
Напряжение на емкости
uC = uCуст + Ae-t/T.
После окончания переходного процесса (заряда конденсатора) ток в цепи прекратится и, как вытекает из выражения (4.40), напряжение на емкости окажется равным напряжению сети:
uCуст = U.
Значение A определяют с помощью второго закона коммутации: при t = 0+ uC = 0.
Таким образом, напряжение на емкости в переходный период
uС = U - Ue-t/T.
Подставив uС в (4.40), получим выражение для тока
| i = | U | e-t/T. |
| r |
На рис. 4.7, б изображены графики напряжения на емкости uС итока i при включении цепи рис. 4.7, а.
Пример 4.4. Определить постоянную времени и длительность переходного процесса при включении цепи, изображенной на рис. 4.7, а. Параметры цепи: r = 10000 Ом, С = 80 мкФ.
Решение. Постоянная времени цепи
Т = rС =10000•80•10-6 = 0,8 с.
Длительность переходного процесса
t = 4T = 4•0,8 = 3,2 с.
