Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
2.5. ЦЕПЬ, СОДЕРЖАЩАЯ ИНДУКТИВНЫЙ ЭЛЕМЕНТ С ИНДУКТИВНОСТЬЮ L
Обмотки (катушки) электрических машин, трансформаторов, магнитных усилителей, электромагнитов, реле, контакторов, индукторов электрических нагревательных устройств и печей переменного тока обладают значительной индуктивностью. В радиотехнических устройствах индуктивные катушки используются для образования колебательных контуров, электрических фильтров и т. п. Параметрами катушек являются активное сопротивление r и индуктивность L. Изменяющийся во времени ток наводит в этих катушках ЭДС самоиндукции, которая по значению во многих случаях заметно больше, чем падение напряжения на активных сопротивлениях.
Рассмотрим вначале катушку, активное сопротивление которой настолько мало, что им можно пренебречь.
Для выяснения процессов, происходящих в цепи с индуктивностью (рис. 2.7, а), допустим, что ток в индуктивности изменяется синусоидально
(2.5)
i = Im sin ωt.
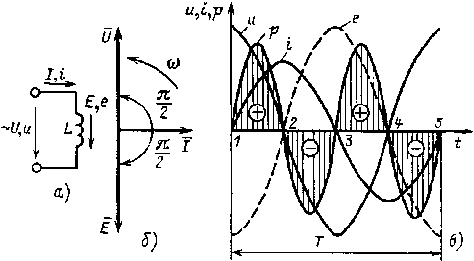 |
Рис. 2.7. Электрическая цепь, содержащая индуктивный элемент с индуктивностью L (а), ее векторная диаграмма (б) и графики мгновенных значений u, i, p (в) |
Ток вызывает в индуктивности ЭДС самоиндукции
(2.6)
eL = - Ldi/dt.
Уравнение, составленное по второму закону Кирхгофа для данной цепи, имеет вид
(2.7)
eL = - и.
Выразив eL и i через их значения из (2.5) и (2.6). найдем напряжение на индуктивности:
| u = L | dIm sin ωt | . |
| dt |
Выполнив операцию дифференцирования, получим
| и = ωLIm cos ωt = ωLIm sin (ωt + | π | ) = Um sin (ωt + | π | ). |
| 2 | 2 |
Из сравнения выражений (2.5) и (2.8) можно сделать вывод, что ток в цепи с индуктивностью и напряжение на индуктивности изменяются по синусоиде, а напряжение опережает по фазе ток на угол 90°.
Векторная диаграмма цепи с индуктивностью изображена на рис. 2.7, б, а графики мгновенных значений тока и напряжения — на рис. 2.7, в.
Напряжение и ток в цепи с индуктивностью, как следует из выражения (2.8), связаны соотношением
Um = ωLIm ,
(2.9)
Im = Um /ωL
Разделив левую и правую части (2.9) на √2, получим закон Ома для цепи переменного тока с индуктивностью.
| I = | U | = | U | . |
| ωL | xL |
Представив в (2.7) ЭДС самоиндукции и напряжение векторами, получим уравнение цепи в векторной форме для действующих значений
Ē = - Ū,
Ē = - Īx‾L.
Таким образом, ЭДС самоиндукции может быть выражена через ток и индуктивное сопротивление. Такой способ выражения ЭДС во многих случаях значительно упрощает анализ цепей с индуктивностью.
Мгновенная мощность цепи с индуктивностью равна
| р = ui = Im sin ωt • Um sin (ωt + | π | ) = | UmIm | sin 2ωt = UI sin 2ωt =Pm sin 2ωt. |
| 2 | 2 |
Мгновенное значение мощности (рис. 2.7, в) изменяется синусоидально с частотой, в 2 раза большей частоты тока. Амплитудное значение мощности
Pm = UI.
Легко показать аналитически и из графика рис. 2.7, в, что среднее значение мощности за период (активная мощность) равно нулю:
|
T | ||||
| P = | ∫ | ui dt = 0. | |||
| 0 |
Для пояснения энергетических процессов в цепи с индуктивностью используем график рис. 2.7, в.
В интервале времени от t = 0 (точка 1) до t= T/4 (точка 2), когда ток в цепи возрастает от 0 до Im, электрическая энергия из сети поступает в индуктивность, преобразуется и накапливается в ней в виде энергии магнитного поля.
Наибольшее значение энергии магнитного поля будет в момент времени, соответствующий точке 2, когда ток достигает амплитудного значения.
| WL = | I2mL | . |
| 2 |
Можно показать, что эта энергия равна заштрихованной площади графика р = f(t) в интервале времени между точками 1 и 2 (отмечена знаком « + ». Действительно,
| T/4 | T/4 |
|
||||||||||||||||||||
| WL = | ∫ | ui dt = | ∫ | |||||||||||||||||||
| 0 | 0 |
В интервале времени между точками 2 и 3 ток в цепи убывает. Энергия магнитного поля преобразуется в электрическую энергию и возвращается в сеть. В момент времени, соответствующий точке 3, ток и энергия магнитного поля равны нулю.
Энергия, отданная в сеть, равна заштрихованной площади графика p = f(t) в интервале времени между точками 2 и 3 (отмечена знаком « - »). Из графиков рис. 2.7, в видно, что площади, определяющие запасенную и отданную энергию, равны. Следовательно, энергия, накопленная в магнитном поле индуктивности в первую четверть периода, полностью возвращается в сеть во вторую четверть периода.
В следующую четверть периода в интервале времени между точками 3 и 4 изменяются направления тока и магнитного потока. Происходит процесс, аналогичный процессу в первую четверть периода: энергия из сети поступает в индуктивность и накапливается в ней в виде энергии магнитного поля. В последнюю четверть периода в интервале времени между точками 4 и 5 энергия магнитного поля возвращается в сеть.
Таким образом, в цепи с индуктивностью происходит непрерывный периодический процесс обмена энергией между сетью (источником энергии) и индуктивностью.
