ЭЛЕКТРОТЕХНИКА

Глава шестая
ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
А. МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ

6.4. ДОПУЩЕНИЯ И ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ ОСНОВНЫХ ЗАКОНОВ МАГНИТНЫХ ЦЕПЕЙ ПРИ РАСЧЕТЕ И АНАЛИЗЕ

Предположим, что имеется некоторая магнитная цепь (рис 6.8, а), содержащая несколько участков из ферромагнитного материала с различными площадями поперечного сечения (S1, S2...) и длинами (l1, l2...); участки l1 и l4, l2 и l5 разделены воздушными зазорами.

Магнитные поля, возникающие под действием МДС обмоток, принято подразделять на основные поля, характеризуемые основными магнитными потоками Ф1, Ф2 и Ф3, и на поля рас­сеяния, характеризуемые некоторыми эквивалентными маг­нитными потоками рассеяния Фр1 и Фр2 (рис. 6.8, а). Основными называются магнитные поля, линии магнитной индукции которых на всем протяжении проходят по магнитопроводу. Линии магнитной индукции полей рассеяния замыкаются вокруг витков соответствующих катушек, проходят большей частью по воздуху и не пересекают витков других катушек. Эквивалентный магнитный поток рассеяния можно определить следующим образом:

где Ф', Ф" и т. д. — магнитные потоки поля рассеяния, пронизы­вающие части w', w" и т, д. общего числа витков wобмотки. Ве­личина Ψр = w'Ф' + w''Ф'' + ... называется потокосцеплением обмотки.

Если степень насыщения ферромагнитного материала и воздушные зазоры невелики, то эквивалентные магнитные потоки рассеяния можно не учитывать, как мы и будем поступать в дальнейшем, При таком допущении магнитный поток любой ветви магнитопровода на всем ее протяжении следует считать одним и тем же. Кроме того, при анализе и расчете магнитных цепей принимают обычно следующие допущения: не учитывают выпучивания линий магнитной индукции в воздушных зазорах, а также их искривлений в узлах разветвления потоков и местах резких перегибов магнитной цепи, считая, что конфигурация линий магнитной индукции совпадает с конфигурацией магнитной цепи (рис. 6.8, б); принимают, что во всех точках площади поперечного сечения любого участка магнитной цепи напряженности магнитного поля, а значит, и магнитные индукции имеют одно и то же значение. Учитывая это, при анализе и расчете магнитных цепей выбирают контуры, совпадающие со средней линией магнитной индукции, показанной на рис. 6.8, в пунктиром.

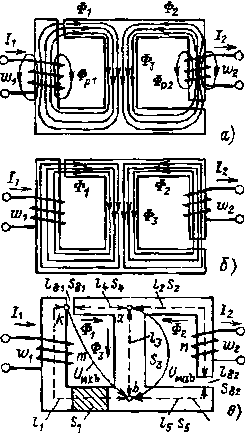Рис.   6.8.   К   пояснению   основных законов магнитных цепей

При расчете и анализе магнитных цепей большое значение имеют положительные направления магнитных потоков и напряженностей магнитного поля, так как в зависимости от них выбираются знаки перед указанными величинами в уравнениях. Положительные направления указываются на расчетных чертежах стрелками.

В случае одной намагничивающей обмотки за положительное направление магнитного потока принимают направление, связанное правилом правоходового винта с положительным направлением тока намагничивающей катушки. В том случае, когда положительное направление магнитного потока не очевидно, что может быть при наличии нескольких намагничивающих обмоток, можно задаться им произвольно. Действительное направление магнитною потока выявляется в этом случае в результате анализа или расчета.

За положительные направления магнитных индукций магнитного поля следует принимать, очевидно, направления, совпадающие с положительными направлениями соответствующих магнитных потоков. Учитывая это, на расчетных чертежах нет необходимости указывать положительные направления всех величин (магнитных потоков, индукций и напряженностей). Достаточно указать, например, только положительные направления магнитных потоков.

Одним из важнейших соотношений для разветвленных магнитных цепей является соотношение между магнитными потоками, согласно которому алгебраическая сумма магнитных потоков ветвей, сходящихся в узле разветвления потоков, равна нулю:

Магнитные потоки, направленные к узлу разветвления потоков, входят в (6.8) со знаком « + », направленные от узла — со знаком « - » или наоборот. Например, при указанных на рис. 6.8, в направлениях потоков для узла aФ1 + Ф2 - Ф3 = 0.

Уравнение (6.8) называют иногда первым законом Кирхгофа для магнитной цепи.

Наряду с уравнением (6.8) при анализе и расчете магнитных цепей широко используется закон полного тока (6.5), который применительно к магнитным цепям соответствующим образом преобразуется. Согласно закону полного тока (6.5) для контура bmkanb при обходе его по часовой стрелке

∫○ Н cos α dl = I1w1 - I2w2.

Заменив интеграл суммой интегралов по участкам и учитывая, что в пределах любого участка с одной и той же площадью поперечного сечения Н = const, а также что на участках, где положительное направление напряженности Н совпадает с направлением обхода контура,
cos α = 1, а где не совпадает, cos α = - 1, после преобразований получим

H1l1 + Hδ1lδ1 + H4l4 - H2l2 - Hδ2lδ2 - H5l5 = I1w1 - I2w2 .

В общем виде закон полного тока для любого замкнутою контура магнитной цепи

Со знаком « + » в (6.9) следует включать напряженности, положительные направления которых совпадают с направлением обхода контура, и токи, положительные направления которых связаны с направлением обхода контура правилом правоходового винта.

Как было показано ранее, напряженность Н можно рассматривать как удельную МДС, необходимую для создания магнитного потока на единице длины контура интегрирования. Тогда, очевидно, произведение Hl можно рассматривать как МДС, необходимую для создания магнитного потока на участке магнитной цепи длиной l. Величину Hl называют разностью скалярных магнитных потенциалов и иногда магнитным напряжением: Hl = Uм . На участке магнитной цепи, не содержащем намагничивающей обмотки, положительное направление магнитного напряжения совпадает с направлением напряженности.

Если в выражении (6.9) МДС F = ΣIw уподобить алгебраической сумме ЭДС, а ΣHl = ΣUм — алгебраической сумме напряжений в электрической цепи, то оно окажется сходным со вторым законом Кирхгофа для электрической цепи. Выражение (6.9) называют иногда вторым законом Кирхгофа для магнитной цепи.

Уравнение (6.9) может быть применено и к замкнутому в геометрическом смысле контуру. Это значит, что часть контура может проходить по стрелке, указывающей положительное направление магнитного напряжения между какими-либо точками контура. Указанная особенность уравнения (6.9) позволяет легко найти магнитное напряжение между интересующими нас точками магнитопровода.

Найдем, например, магнитное напряжение между точками k и b (см. рис 6.8, в) Выбрав положительное направление искомого магнитного напряжения Uмkb, например, как показано на рисунке, и обходя контур аbkа по часовой стрелке, получим

H3l3- Uмkb+ Hδ1lδ1 + H4l4 = 0.

Uмkb = H3l3+ Hδ1lδ1 + H4l4.

Для определения Uмkb можно воспользоваться также контуром bmkb или bkand. Например, при обходе по часовой стрелке контура bmkb найдем, что Uмkb = I1w1 - H1l1.

Как видно, в случае, когда контур проходит через участок, содержащий намагничивающую обмотку, в выражении магнитного напряжения появляется МДС обмотки.

Следует заметить, что если в выражении магнитного напряжения Uм = HI заменить H на B/μа, а В — на Ф/S, то получим

Uм = ФRм,

Уподобив Ф току, a Rм — сопротивлению электрической цепи, можно считать, что выражение Uм = ФRм аналогично закону Ома для пассивного участка электрической цепи. Очевидно, любой член в левой части (6.9) может быть заменен выражением ФRм.