ЭЛЕКТРОТЕХНИКА

Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

2.3 ВЕКТОРНЫЕ ДИАГРАММЫ

Для упрощения анализа и расчета цепей переменного тока целесообразно использовать векторы.

В электротехнике векторами изображаются изменяющиеся синусоидально ЭДС, напряжения и токи, но в отличие от векторов, которыми изображались силы и скорости в механике, эти векторы вращаются с постоянной угловой частотой ω и не означают направление действия.

Допустим, что радиус-вектор ОА (рис. 2.3,а), представляющий собой в определенном масштабе амплитудное значение ЭДС Ет , вращается с постоянной угловой частотой ω = 2πf против часовой стрелки. Проекция вектора ОА на вертикальную ось (ось у) будет равна

Выразив ОА через амплитудное значение ЭДС Ет и α через ωt, получим выражение мгновенного значения ЭДС, изменяющейся синусоидально:

График мгновенных значений ЭДС изображен на рис. 2.3,б. За начало отсчета выбран момент времени, когда радиус-вектор совпадает с горизонтальной осью (ось х).

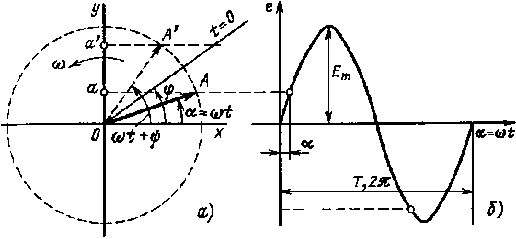Рис.  2.3.  Вращающиеся векторы (а) и график  мгновенных значений синусоидальной ЭДС (б)

Если в момент t = 0 радиус-вектор ОА совпадает с линией, расположенной под углом ψ к оси х, то проекция Оа' и, следовательно, ЭДС будут соответственно равны

Аналогично можно представить в виде векторов, вращающихся против часовой стрелки с постоянной угловой частотой ω, напряжение и ток.

Расчет цепей синусоидального тока производят в действующих значениях ЭДС, напряжений и токов. При этом суммирование Е, U, I проще осуществить с помощью вращающихся векторов, вместо того чтобы, сложив мгновенные значения е, и, i, определить действующие значения результирующих Е, U, I интегрированием гармонических функций. Адекватность этих действий можно обосновать так.

Допустим, что в каком-то узле цепи переменного тока (рис. 2.4, а) известны значения токов i1 и i2:

Требуется определить ток i.

На основании первого закона Кирхгофа мгновенное значение тока

т. e.

Ток i можно определить аналитически путем тригонометрических преобразований  или графически сложением графиков мгновенных значений токов i1 и i2, как это сделано на рис. 2.4, б. Результирующий ток также изменяется синусоидально и в соответствии с рис. 2.4, б

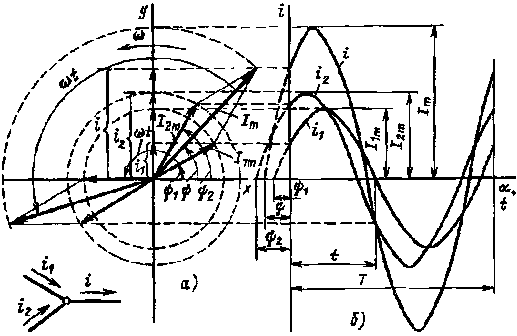Рис. 2.4. Сложение синусоидальных токов с помощью векторов (а): графики мгновенных значений токов (б)

Значительно проще произвести сложение токов i1 и i2, если изобразить амплитуды токов в виде векторов и сложить их по правилу параллелограмма. На рис. 2.4, а амплитуды токов I1m и I2m изображены в виде векторов под углами начальных фаз ψ1 и ψ2 относительно оси х. По прошествии времени t векторы повернутся на угол α = ωt. Проекции амплитуд на ось у составят

Сложив векторы I1m и I2m по правилу параллелограмма (см. рис. 2,4, а), получим амплитуду результирующего тока Im . Сумма проекций токов I1m и I2m равна проекции результирующего тока Im :

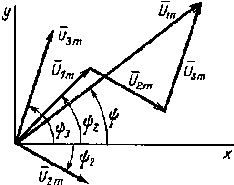Рис  2.5.  Векторная  диаграмма напряжений

Полученное выражение соответствует первому закону Кирхгофа  для  рассматриваемого узла  цепи   (см.   рис.   2.4, а). Из рис. 2.4. а видно, что взаимное расположение векторов I1m, I2m и Im в любой момент времени остается неизменным, так как они вращаются с постоянной угловой частотой ω. Аналогично можно определить сумму нескольких изменяющихся синусоидально с одинаковой частотой напряжений или ЭДС Например, в последовательной цепи переменного тока действуют три напряжения:

Сумму u = u1 + u2 + u3 напряжений можно определить путем сложения векторов их амплитуд (рис. 2.5) и последующей записи результирующего напряжения u = Um sin (ωt + ψ).

Совокупность нескольких вращающихся векторов, соответствующих уравнениям электрической цепи, называется векторной диаграммой.

Обычно векторные диаграммы строят не для амплитудных, а для действующих значений. Векторы действующих значений отличаются от векторов амплитудных значений только масштабами, так как

При построении векторных диаграмм обычно один из исходных векторов располагают на плоскости произвольно, остальные же векторы — под соответствующими углами к исходному. При этом в подавляющем большинстве случаев можно обойтись без нанесения осей координат х и у.