Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.4. ПОДКЛЮЧЕНИЕ КАТУШКИ С r, L К СЕТИ С СИНУСОИДАЛЬНЫМ НАПРЯЖЕНИЕМ
Уравнение для цепи рис. 4.4, а, составленное по второму закону Кирхгофа, имеет вид
е =ir - и.
Выразив в (4.26) напряжение u через амплитудное значение и ЭДС е - через индуктивность и скорость изменения тока, получим дифференциальное уравнение
L di/dt + ir = Um sin (ωt + ψ).
Решение дифференциального уравнения для свободного тока
L diсв /dt + iсв r = 0
iсв = Aept.
Показатель степени р определяют из характеристического уравнения Lp + r = 0:
| р = - | r | = - | 1 | , |
| L | T |
Ток в цепи в переходный период
i = iуст + Ae-t/T.
Принужденный ток в цепи после окончания переходного процесса определяют по закону Ома:
| iуст = | Um | sin (ωt + ψ - φ), |
| z |
| z = √r2 + xL2 , φ = arccos | r | , |
| z |
Значение A определяют из (4.27) с помощью первого закона коммутации:
при t = 0+ i(0+) = i(0-) = 0 и
| 0 = | Um | sin(ψ - φ) + A, |
| z |
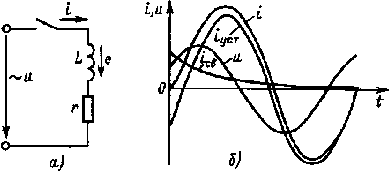 |
Рис. 4.4. Зависимости i(t), iуст(t), iсв(t), u(t) (б) при подключении цепи r, L, (а) к сети с синусоидальным напряжением |
откуда
| А= - | Um | sin (ψ - φ), |
| z |
После подстановки А в (4.27) получим
| i = | Um | sin (ωt + ψ - φ) - | Um | sin (ψ - φ) e-t/T. |
| z | z |
Из анализа (4.28) вытекает, что характер переходного процесса зависит от ψ и φ. На рис. 4.4, б изображены графики мгновенных значений напряжения, установившегося, свободного и полного токов при включении цепи рис. 4.4, а. Следует отметить, что если в момент включения при
t = 0+, ψ - φ = 0, или ψ = φ, то принужденный ток равен нулю, поэтому свободный ток не возникает и в цепи после включения сразу наступает установившийся режим.
