ЭЛЕКТРОТЕХНИКА

Глава шестая
ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
А. МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ

6.7. РАЗВЕТВЛЕННЫЕ МАГНИТНЫЕ ЦЕПИ

6.7.1. Основные соотношения. Когда в разветвленной магнитной цепи магнитные потоки возбуждаются одной обмоткой, направление их при заданном токе определяется однозначно по правилу правоходового винта. Если же для возбуждения потоков используется несколько обмоток, то магнитные потоки могут быть направлены поразному в зависимости от направлений и значений МДС обмоток, а также от параметров магнитопровода.

Рассмотрим в качестве примера возможные направления магнитных потоков в магнитной цепи, изображенной на рис. 6.8.

При I1 > 0 и I2 = 0 магнитные потоки Ф1 и Ф3 будут направлены так, как показано на рисунке (Ф1 > 0 и Ф3 > 0), а поток Ф2 — в противоположную сторону (Ф2 < 0). При I1 = 0 и I2 > 0 потоки Ф2 > 0 и Ф3 > 0, а Ф1 < 0.

Изменяя I1 при I2 = const или I2 при I1 = const, можно получить Ф1 <> 0 и Ф2 <> 0; магнитный поток Ф3 при любых токах I1 > 0 и I2 > 0 будет направлен так, как показано на рисунке.

Так как в каждой ветви разветвленной магнитной цепи магнитный поток имеет одно и то же значение, между магнитными индукциями, а также между напряженностями участков любой ветви существуют соотношения, полученные ранее для неразветвленной цепи.

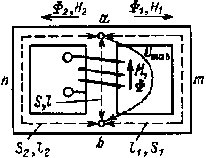Рис. 6.14. К анализу соотношений в разветвленных магнитных цепях

Рассмотрим  соотношения   между   напряженностями,   магнитными индукциями и потоками двух ветвей amb и аnb, не содержащих обмоток (рис.  6.14). По закону полного тока для контуров аmbа и аnbа имеем

H1l1 - Umab = 0 и  H2l2 - Umab = 0.

Из полученных уравнений следует, что

Если l1 = l2, то независимо oт площадей поперечного сечения S1 и S2, а также марки ферромагнитных материалов ветвей получим Н1 = Н2. Если ветви выполнены из одинакового ферромагнитного материала, то при H1 = Н2 и
В1 = В2. Магнитные потоки ветвей в случае В1 = В2 будут равны лишь при равенстве площадей, так как Ф1 = В1S1, a
Ф2 = B2S2.

Если в магнитной цепи l1 > l2, то согласно (6.15) H1 < H2 и, следовательно, В1 < В2. Количественное соотношение между потоками зависит от соотношений между индукциями и площадями :

Ф1	=	В1S1	;
Ф2		В2S2

Может   оказаться,   например,   что   Ф1 > Ф2   при   В1 < В2 .

На соотношение напряженностей, магнитных индукций и потоков существенное влияние оказывают воздушные за­зоры. Допустим, что во вторую ветвь введен воздушный зазор длиной lδ. Тогда

Так  как обычно  Hδ >> H2,   вместо  (6.16)   можно  написать

H1l1 = H2l2 + Hδlδ,

откуда следует, что при l1 = l2 H1 > H2; как правило, Hδlδ в несколько раз превышает H2l2, поэтому напряженность H2 в ветви с воздушным зазором в несколько раз меньше напряженности H1.

6.7.2. Последовательность расчета симметричных магнитных цепей.

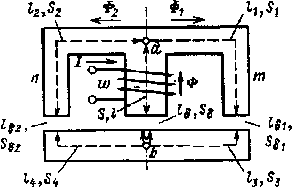Рис. 6.15. Разветвленная симметричная магнитная цепь

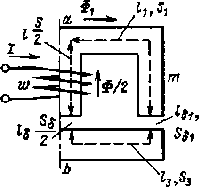Рис. 6.16. К расчету разветвленной симметричной магнитной цепи

Предположим, что имеется разветвленная симметричная магнитная цепь (рис. 6.15) некоторого электромагнитного устройства.

В силу симметрии магнитной цепи и выражения (6.8) можно утверждать, что

Ф1 = Ф2 = Ф/2.

Вследствие простого соотношения между магнитными потоками расчет разветвленных симметричных магнитных цепей производится практически в том же порядке, что и расчет неразветвленных магнитных цепей.

Обычно при расчете симметричную магнитную цепь делят мысленно на две одинаковые части по оси симметрии ab и производят расчет одной ее половины (рис. 6.16).

6.7.3.  Последовательность расчета несимметричных магнитных цепей.

Некоторая сложность расчета несимметричных магнитных цепей объясняется тем, что количественные соотношения между магнитными потоками   ветвей   остаются   неизвестными   до   определения   потоков.

Расчет несимметричных магнитных цепей производится графо­аналитическим методом с использованием соотношения между магнитными потоками в разветвленных цепях (6.8), закона полного тока (6.9) и вб. а. х., методика расчета которых была рассмотрена выше. В зависимости от исходных данных последовательность расчета несимметричных цепей несколько изменяется.

Рассмотрим в качестве примера последовательность расчета магнитной цепи, изображенной на рис. 6.8, если требуется определить МДС I1w1 при заданной магнитной индукции Вδ2 и известной МДС I2w2.

Зная Вδ2, нетрудно найти магнитный поток Ф2 = Вδ2Sδ2, а затем подсчитать магнитное напряжение Umab :

Umab = I2w2 - H2l2 - Hδ2lδ2 - H5l5.

Построив с помощью уравнения Umab = Н3l3 вб. а. х. Ф3(Umab) и зная магнитное напряжение Umab, легко определить магнитный поток Ф3.

Зная потоки Ф2 и Ф3, найдем поток Ф1 = Ф3 — Ф2. После этого можно определить МДС I1w1.

I1w1 = Н1l1 + Hδ1lδ1 + Н4l4 + Umab .