ЭЛЕКТРОТЕХНИКА

Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

4.5. ОТКЛЮЧЕНИЕ КАТУШКИ С r, L ОТ СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ

Допустим, что до отключения в цепи рис. 4.5, а был установившийся ток I = U/r и энергия магнитного поля катушки составляла

Казалось бы, после размыкания выключателя ток должен мгновенно прекратиться. Однако на основании первого закона коммутации при t = 0+ ток сохраняет свое прежнее значение.

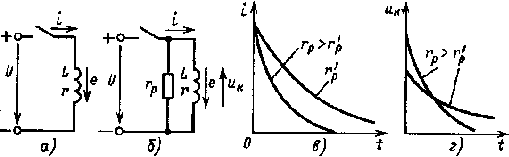Рис. 4.5. Отключение цепи r, L(а) от сети постоянного тока; без разрядного резистора (а), с разрядным резистором (б); зависимости   i(t)  (в)  и  uL(t)(г)  при  отключении   цепи  r,   L с  разрядным резистором

Возникает как будто несоответствие: цепь разомкнута, ток есть. В действительности при размыкании выключатели происходит следующее. Ток уменьшается, и в катушке индуктируется значительная ЭДС. При этом напряжение между контактами выключателя, равное сумме напряжения сети и ЭДС самоиндукции, пробивает воздушный промежуток между контактами — возникает электрическая дута и электрическая цепь оказывается замкнутой. По мере увеличения расстояния между контактами сопротивление дуги возрастает, ток и ЭДС уменьшаются и цепь оказывается разомкнутой. За время переходного процесса энергия магнитного поля катушки выделяется в виде теплоты в электрической дуге и сопротивлении катушки.

Переходный процесс в этом случае получается довольно сложным вследствие того, что сопротивление дуги нелинейное и изменяется во времени (его анализ выходит за рамки данного учебного пособия).

Отключение цепи с индуктивностью вызывает обгорание контактов размыкающего устройства и появление значительных ЭДС и напряжения на выводах катушки, превышающих в несколько раз напряжение сети (это может привести к пробою изоляции катушки).

Во избежание этого в силовых цепях, обладающих значительной индуктивностью (обмотки возбуждения генераторов и двигателей постоянного тока, синхронных двигателей, магнитных плит и т. п.), параллельно обмоткам включают разрядные резисторы (рис. 4.5, б).

В этом случае после отключения выключателя катушка индуктивности (r, L) оказывается замкнутой на разрядное сопротивление rр . Ток в цепи будет убывать значительно медленнее. По этой причине значение возникающей ЭДС будет существенно меньше, чем без разрядного резистора, и возникшая слабая дуга исчезает почти мгновенно. В последующих рассуждениях и выводах предполагается, что дуга между контактами не возникает и цепь размыкается мгновенно.

Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид

Заменив e в (4.29), получим

Решением дифференциального уравнения будет выражение

Из характеристического уравнения pL+ (r + rp)= 0 определяют показатель степени р:

р  = -	r + rp	= -	1	.
	L		Т

Подставив это выражение в (4.31), получим

где Т = L/(r + rp) — постоянная времени цепи.

Значение А определяют из начальных условий на основании первого закона коммутации: при t = 0+

Выражение тока в цепи имеет вид

Подставив   в   (4.29)   значение   i   из   (4.32),   получим   ЭДС

е =	U	(r + rp)e-t/T = Iнач(r + rp)e-t/T.
	r

Напряжение на  выводах  катушки  равно  напряжению  на разрядном резисторе:

uк = irр =	U	rpe-t/T - Iнач rpe-t/T.
	r

В начальный момент при t = 0+

а

Из выражений (4.33) и (4.34) вытекает, что начальные значения eнач и uк.нач зависят от сопротивления разрядного резистора. При больших значениях rр они могут оказаться чрезмерно большими и опасными для изоляция установки.

На рис. 4.5, в изображены графики i(t) и uк(t) катушки после отключения цепи для двух значений rр, rр > r'р.

На практике обычно выбирают rр в 4—8 раз больше собственного сопротивления обмотки индуктивной катушки:

Пример 4.2. Определить начальные значения ЭДС самоиндукции и напряжения на катушке при отключении цепи, изображенной на рис. 4.5, б, для двух значений rр: а) rр = 4r; б) rр = 20r. Параметры цепи: r =100 Ом, U = 400 В.

Решение. Начальное значение тока в катушке

Начальные значения ЭДС:

а) Енач = Iнач (r + rp) = 4 (100 + 4•100) = 2000 В; Uк.нач = Iнач rp = 4•400=1600 В;

б) Енач = Iнач (r + rp) = 4(100 + 20•100) = 8400 В; Uк.нач = Iнач rp = 4•20•100 = 8000 В.