Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.9. РАЗРЯД КОНДЕНСАТОРА НА КАТУШКУ С r, L
Допустим, что конденсатор С (рис. 4.9, a) был включен а сеть постоянного тока и, следовательно, заряжен до напряжения сети U.
После переключения выключателя из положения а в положение б конденсатор окажется замкнутым на цепочку r, L. Под действием напряжения на конденсаторе uC в цепи возникнет ток и конденсатор начнет разряжаться. Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид
e = ir - uC.
Выразив в (4.49) e через ток и индуктивность
e = - L di/dt,
| i = - С | duC | , duC = - | i dt | , uC = - | 1 | ∫i dt, |
| dt | C | C |
| -L | di | - ir - | 1 | ∫i dt = 0. |
| dt | C |
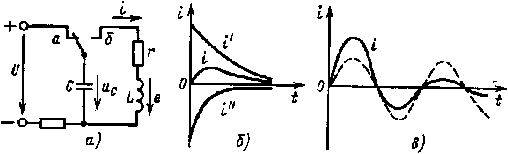 |
Рис.4.9. Зависимости i(t) при апериоди- ческом (б) и коле- бательном (в) раз- рядах конденсато- ра на сопротивле- ние r и индук ти-вность L цепи (a) |
Взяв производную от левой и правой частей уравнения, получим дифференциальное уравнение второго порядка без правой части
| d2i | + | r | di | + | i | = 0. |
| dt2 | L | dt | CL |
Решением дифференциального уравнении является выражение
i = A1ep1t + A2ep2t.
| Корнями характеристического уравнения р2 + | r | р + | 1 | = 0 будут |
| L | CL |
| p1.2 = - | r | ± | √ | ( | r | )2 | - | 1 | . |
| 2L | 2L | CL |
Обозначив r/2L = β и 1/LC = ω02, получим
p1.2= - β ± √β2 - ω02 = - β ± γ.
γ = √β2 - ω02.
Значения A1 и A2 определяют из начальных условий с помощью первого и второго законов коммутации.
По первому закону коммутации при t = 0+ i = 0 и из (4.51) вытекает,
A1 = - A2.
По второму закону коммутации при t = 0+
uC = U.
Таким образом, в первый момент после замыкания цепи, как следует из (4.49), ЭДС равна
- U, так как ir = 0.
e = - Ldi/dt = -U
di/dt = U/L.
di/dt = А1р1ep1t + А2р2еp2t = U/L.
При t = 0+
А1р1 + А2р2 = U/L.
Из совместного решения (4.52) и (4.53) получим
| А1 = | U | = - А2. |
| L(р1 - р2) |
Выразим р1 и р2 через β и γ:
| А1 = | U | , А2 = - | U | . |
| 2Lγ | 2Lγ |
Следовательно, выражение для тока в переходный период будет иметь вид
| i = | U | ep1t - | U | еp2t. |
| 2Lγ | 2Lγ |
Характер переходного процесса зависит от соотношения параметров r, L, С цепи и определяется корнями характеристического уравнения.
При 1/CL < (r/2L)2 корни будут действительными:
р1 = - β + γ, р2 = - β - γ.
| i = | U | e(- β + γ)t - | U | e- (β + γ)t = i' + i". |
| 2Lγ | 2Lγ |
Графики тока для этого случая изображены на рис. 4.9, б. При (r/2L)2 < 1/LC корни характеристического уравнения оказываются комплексными сопряженными:
р1 = - β + jω, р2 = - β - jω,
Значения А1 и А2 в этом случае будут равны
| А1 = | U | , А2 = - | U | . |
| 2jωL | 2jωL |
Подставив значения p1, p2 и А1, А2 в (4.51), получим
| i = | U | [e(- β + jω)t - e(- β - jω)t] - | U | [ejωt - e-jωt]е-βt = |
| 2jωL | 2jωL |
| = | U | е-βt 2jsin ωt = | U | sin ωtе-βt. |
| 2jωL | ωL |
На рис. 4.9, в изображен график i(t).Ток изменяется по закону, представляющему собой произведение синусоиды с амплитудой UjωL на показательную функцию. В идеальном случае, когда r = 0, возникнут синусоидальные колебания с неизменной амплитудой.
Действительно, при r = 0, β = 0, ω = ω0 ток
| i = | U | sin ω0t, |
| ω0L |
ω0 = 1/√LC, Т = 1/f = 2π/ω0.
На рис. 4.9, в пунктирной линией изображен график незатухающих колебаний.
