ЭЛЕКТРОТЕХНИКА

Глава пятая
ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ЭДС, ТОКИ И НАПРЯЖЕНИЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

5.2. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ПЕРИОДИЧЕСКИХ НЕСИНУСОИДАЛЬНЫХ ВЕЛИЧИН

Периодические несинусоидальные величины могут быть представлены временными диаграммами, тригонометрическим рядом Фурье, а также эквивалентными синусоидами. Наиболее наглядными, дающими полное представление о несинусоидальной величине являются временные диаграммы, т. е. графики зависимости  мгновенных  значений  от  времени  (рис.   5.2 — 5.4).

Несинусоидальные ЭДС, токи и напряжения, с которыми приходится встречаться в электротехнике и промышленной электронике, являются периодическими функциями, удовлетворяющими условиям Дирихле и, следовательно, могут быть представлены тригонометрическим рядом Фурье:

где A0 — постоянная  составляющая;  A1m sin(ωt + ψ1) — основная или первая гармоника, частота которой ω = 2π/Т равна частоте исследуемой несинусоидальной величины; Akm sin(kωt + ψk) — высшие k-е гармоники; Akm и ψk — амплитуды и начальные фазы k-x гармоник.

Тригонометрический ряд может быть представлен как в виде суммы синусов (синусный ряд), так и суммы косинусов (косинусный ряд) гармонических составляющих.

В зависимости от характера реальной кривой f(ωt) тригонометрический ряд может не содержать постоянней составляющей, четных или нечетных высших гармоник, а также начальных фаз. Например, тригонометрические ряды Фурье некоторых несинусоидальных напряжений имеют вид:

напряжение на нагрузке при однополупериодном выпрямлении (см. рис. 5.2, а)

u(t) =	Umax	(1 +	π	cos ωt +	2	cos 2ωt -	2	cos 4ωt + ... );
	π		2		3		15

напряжение на нагрузке при двухполупериодном выпрямлении (см. рис; 5.2, б)

u(t) =	2Umax	(1 +	2	cos 2ωt -	2	cos 4ωt +	2	соs 6ωt - ... );
	π		3		15		35

напряжение на нагрузке при трехфазном выпрямлении (см. рис. 5.2, в)

u(t) =	3Umax	(1 +	2	cos 6ωt -	2	cos 12ωt +	2	соs 18ωt - ... );
	π		35		143		323

напряжение треугольной формы (ем. рис. 5.3, а)

u(t) =	8Umax	( sin ωt -	1	sin 3ωt +	1	sin 5ωt -	1	sin 7ωt + ... );
	π2		9		25		49

напряжение прямоугольной формы (см. рис. 5.3, б)

u(t) =	4Umax	( sin ωt +	1	sin 3ωt +	1	sin 5ωt +	1	sin 7ωt + ... );
	π		3		5		7

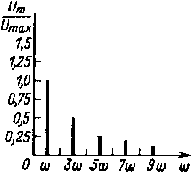Рис. 5.5. Диаграмма амплитудно-частотного спектра

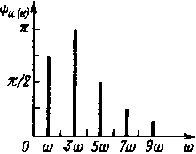Рис. 5.6. Диаграмма фазочастотного спектра

В практических расчетах цепей с несинусоидальными ЭДС, токами и напряжениями их мгновенные значения приближенно отображают конечным рядом Фурье (3 — 7 членов ряда). Число членов  ряда  определяется  необходимой   точностью  расчета.

Характеристика несинусоидальных величин, представленных рядом Фурье, может быть осуществлена графически с по­мощью диаграмм амплитудно-частотного (рис. 5.5) и фазоча­стотного (рис. 5.6) спектров. Данные диаграммы характеризуют форму несинусоидальных кривых, причем первая диаграмма показывает спектральный состав по амплитудам, т. е. представ­ляет зависимость амплитуд гармоник в относительных еди­ницах от частоты, вторая диаграмма выражает зависимость начальных фаз гармоник от частоты.

Периодические несинусоидальные ЭДС, напряжения и токи могут быть представлены так же эквивалентными синусоидами (см. § 5.5).