Глава шестая
ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
Б. МАГНИТНЫЕ ЦЕПИ С ПЕРЕМЕННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ
6.11. ФОРМЫ КРИВЫХ ЭДС е, МАГНИТНОГО ПОТОКА Ф, ТОКА i И МГНОВЕННОЙ МОЩНОСТИ ρ ИДЕАЛИЗИРОВАННОЙ ОБМОТКИ
В соответствии с уравнением (6.21) обмотка с ферромагнитным магнитопроводом (см. рис 6.21, а) может быть заменена для удобства анализа устройством, изображенным на рис. 6,21, б. Часть этого устройства, состоящую из обмотки, расположенной на ферромагнитном магнитопроводе, будем называть в дальнейшем идеализированной обмоткой.
Предположим, что к идеализированной обмотке подведено напряжение u' (см. рис. 6.21, б), изменяющееся по синусоидальному закону:
u' = Um' sin (ωt + π/2).
Так как согласно второму закону Кирхгофа u' = - е, то
e = Em' sin (ωt - π/2).
где Еm = Um' и, очевидно, Е = U' .
Чтобы получить закон изменения магнитного потока, воспользуемся выражением
е = - wdФ/dt, из которого после замены ЭДС согласно (6.23) найдем| Ф = - ∫ | e | dt = - ∫ | Em sin(ωt - π/2) | dt = | Em | sin ωt + Ф0, |
| w | w | ωw |
Так как напряжение u' не имеет постоянной составляющей, то не будут иметь постоянных составляющих также ток i и МДС iw. Поэтому следует считать, что и Ф0 = 0. Величина Em /ωw представляет собой амплитуду магнитного потока
| Em | = Фт. |
| ωw |
Учитывая сказанное, вместо (6.24) окончательно будем иметь
Ф = Фт sin ωt.
На основании полученных соотношений для идеализированной обмотки можно утверждать, что независимо от свойств ферромагнитного материала и особенностей магнитопровода, в частности от того, есть или отсутствует воздушный зазор, справедливо следующее:
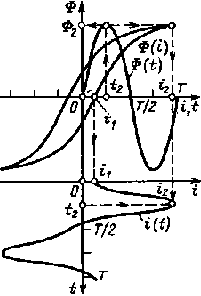 |
| Рис. 6.25. К вопросу построения графика тока идеализированной обмотки |
при синусоидальном напряжении u' ЭДС е и магнитный поток Ф изменяются также по синусоидальному закону;
при указанных на рис. 6.21 положительных направлениях ЭДС отстает по фазе от напряжения на угол π, а от магнитного потока — на угол π/2;
амплитуда магнитного потока прямо пропорциональна амплитуде ЭДС, а значит и амплитуде напряжения, поскольку Ет = Um';
изменение числа витков w или частоты переменного тока
f = ω/2π при заданном значении Um' приводит к изменению амплитуды магнитного потока Фm.
Из выражения (6.25) нетрудно получить широко распространенную формулу действующего значения ЭДС
| Е = | Еm | = | ωwФm | = | 2π | fwФm, |
| √2 | √2 | √2 |
Е = 4,44fwФm = 4,44fwBmS,
Чтобы построить график i(r), можно воспользоваться графиком Ф(t) и магнитной характеристикой Ф(i) обмотки (рис. 6.25).
Для построения графика Ф(t), который не зависит от свойств ферромагнитного материала и параметров магнитопровода, следует воспользоваться выражениями (6.25) и (6.26), учитывая, что Ет = Um'.
Магнитную характеристику Ф(i) можно построить путем расчета магнитной цепи (рис. 6.21,б), используя в качестве кривой намагничивания В (Н) динамический цикл гистерезиса, соответствующий заданной частоте f и амплитудному значению магнитной индукции Вт, зависящему согласно (6.27) и равенству Е = U' от действующего значения напряжения U'. Рассмотрим последовательность расчета магнитной цепи (рис. 6.21, б), считая, что lδ = 0, а l— общая длина средней линии магнитной индукции.
Задавшись, например, магнитным потоком Ф1, определяем магнитную индукцию B1 = Ф1/S, по кривой намагничивания В (Н) находим напряженность магнитного поля Н1, с помощью закона полного тока для мгновенных значений напряженности и тока H1l = i1w подсчитываем ток
i1 = Н1l/w. Чтобы построить магнитную характеристику, необходимо проделать указанные операции для различных значений магнитного потока в пределах периода его изменения. Поскольку Ф = ВS, a i = Нl/w, магнитная характеристика будет подобна динамической петле гистерезиса.
Построение графика i(t) с помощью графиков Ф(t) и Ф(i) (рис. 6.25) может быть произведено в таком порядке. Задаемся, предположим, временем t1 = 0; пользуясь графиком Ф(t), находим Ф1 = 0, а используя график Ф(i), определяем ток i1; в системе координат i, t при t1 = 0 откладываем значение тока i1. Задавшись временем t2 = T/4, по графику Ф(t) находим Ф2, а по графику Ф(i) — ток i2. В системе координат i, t при t2= Т/4 откладываем значение тока i2. Для построения графика i(t) необходимо определить токи при различных значениях времен в пределах периода Т.
Изучив рассмотренную методику построения графика i(t), нетрудно сделать заключение о том, что для построения указанного графика нет необходимости строить график Ф(i); достаточно иметь зависимость Ф (t) и динамический цикл гистерезиса. График Ф(i) был использован для большей наглядности.
Как следует из выражений (6.22), (6.23) и (6.26), а также графика i(t), при синусоидальных u', е и Ф ток iидеализированной обмотки получается несинусоидальным. Можно показать, что он будет тем сильнее отличаться от синусоидального, чем больше степень насыщения ферромагнитного материала магнитопровода при амплитудном значении магнитного потока и шире динамическая петля гистерезиса.
Построение графика i'(t) при наличии воздушного зазора (lδ ≠ 0) отличается лишь тем, что для определения тока i' следует использовать закон полного тока в виде Hl + Hδlδ = i'w.
Чтобы составить представление об изменении максимального тока обмотки при введении воздушного зазора в магнитопровод, запишем уравнение по закону полного тока для максимальных значений напряженностей и тока Hmaxl+ Hδmlδ = I'maxw
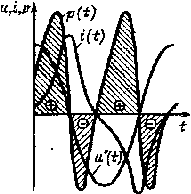 |
| Рис. 6.26. Графики u'(t), i'(t) и р(t) идеализированной обмотки |
Последнее уравнение можно переписать в такой форме:
Hmax l + Hδm lδ = Imax w + Iδm wδ,
где Imax w = Hmax l, Iδm wδ = Hδm lδ. Очевидно, I'max = Imax + Iδm.Как известно, при Вδm = Вт Нδm >> Нmax . Поэтому даже при воздушных зазорах Hδm lδ > Hmax l (см. пример 6.1), следовательно, и Iδm > Imax . Таким образом, ток I'max при lδ ≠ 0 обычно больше тока Imax при lδ = 0 на Iδm > Imax.
Нетрудно показать, что график i'(t) при lδ ≠ 0 меньше отличается от синусоиды, чем график i(t) при lδ = 0. Действительно, согласно закону полного тока для мгновенных значений напряженностей и токов Hl + Hδlδ = i'w = iw+ iδw. Очевидно i' = i+ iδ .
Если Um' имеет то же значение, что при lδ = 0, то Фm также не изменится. Поэтому график i(t) несинусоидального тока останется прежним. Поскольку зависимость Ф(i) для воздушного зазора линейная, а Ф(t) представляет собой синусоиду, ток iδ будет также синусоидальным. Суммирование токов i и iδ для получения графика i'(t) приведет вследствие этого к тому, что график i'(t) будет меньше отличаться от синусоиды, чем график i(t) при lδ = 0.
Из графика тока (рис. 6.25) следует, что при Ф = 0, а значит, при u' = ± Um' ток i не равен нулю, что является признаком потребления обмоткой активной мощности. Чтобы составить более отчетливое представление об энергетических процессах идеализированной обмотки, обратимся к рис. 6.26, на котором приведены графики u'(t), i(t), а также график мгновенной мощности р(t), построенный в соответствии с формулой р = u'i. Как видно, в течение большей части периода р > 0. Поэтому если подсчитать потребляемую активную мощность
| P' = | 1 | ∫ p dt = | 1 | ∫ u'i dt, |
| T | T |
то окажется, что Р' ≠ 0. Поскольку идеализированная обмотка не имеет активного сопротивления, следует признать, что активная мощность идеализированной обмотки равна потерям мощности в ферромагнитном материале магнитопровода, Р' = ΔРс. Таким образом, в отличие от обмотки без ферромагнитного магнитопровода идеализированная обмотка с ферромагнитным магнитопроводом кроме реактивной мощности, необходимой для возбуждения магнитного потока, потребляет еще и активную мощность, вызванную процессами, связанными с перемагничиванием ферромагнитного материала и возникновением в нем вихревых токов.
