Глава первая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1.7. НЕКОТОРЫЕ ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ ЗАКОНОВ ОМА И КИРХГОФА ПРИ РАСЧЕТЕ И АНАЛИЗЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Как известно, согласно закону Ома в замкнутой неразветвленной электрической цепи (см. рис. 1.1, а)
| I = | Е | . |
| r0 + r1 + r2+ r3 |
А в любом пассивном элементе цепи, например с сопротивлением r2 (рис. 1.1,a),
I = U2/r2 .
Выражение (1.3) справедливо при совпадающих направлениях ЭДС Е и тока I, а выражение (1.4) - при совпадающих направлениях напряжения, U и тока I, что и следует учитывать при нанесении на схеме стрелок, указывающих положительные направления, в случае использования закона Ома.
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, соединенных в любой узловой точке электрической цепи, равна нулю, т. е.
ΣI = 0.
Со знаком « + » в уравнение следует включать токи, положительные направления которых обращены к узлу, со знаком « — » — положительные направления которых обращены от узла (можно и наоборот). Например, для узла А (рис. 1.2)
I1 + I2 + I3 - I4 - I5 = 0.
Согласно второму закону Кирхгофа в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех резистивных элементах контура, т. е.
ΣЕ = ΣIr.
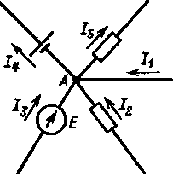 |
| Рис. 1.2. К пояснению первого закона Кирхгофа |
Часто в электрических цепях встречаются элементы, между выводами которых имеются те или иные напряжения U (например, напряжение сети, напряжение, снимаемое с делителя напряжения, и т. д.).
Учитывая это, вместо (1.6) удобнее использовать следующую форму записи второго закона Кирхгофа:
ΣЕ = ΣIr + ΣU.
При этом ЭДС, напряжения и токи, положительные направления которых совпадают с направлением обхода контура при составлении уравнения (1.7), следует включать в уравнение со знаком « + », а те, положительные направления которых не совпадают с направлением обхода контура, — со знаком «-» (можно и наоборот).
При подстановке в уравнения (1.5)—(1.7) числовых значений ЭДС, напряжений и токов следует учитывать, что указанные величины могут быть как положительными, так и отрицательными, что повлияет па окончательные знаки перед ЭДС, напряжениями и токами.
Следует заметить, что уравнение (1.7) может быть применено и к такому контуру, который замкнут в геометрическом смысле. Это значит, что часть контура может проходить по стрелке, указывающей положительное направление напряжения между какимилибо точками. Таким образом, можно всегда записать уравнение для напряжения между двумя любыми точками электрической цепи.
При составлении уравнений по второму закону Кирхгофа следует включать в них либо ЭДС и падение напряжения во внутренних сопротивлениях активных элементов, либо только их напряжения.
Например, для электрической цепи рис. 1.1, а по второму закону Кирхгофа можно написать
E = Ir0 + I(r1 + r2 + r3)
0 = I(r1 + r2 + r3) - Uab .
Исключением является случай, когда уравнение составляется для контура, проходящего через активный элемент и стрелку, указывающую положительное направление напряжения этого же элемента. Только в этом случае в уравнение войдут ЭДС,
| Рис. 1.3. К пояснению второго закона Кирхгофа | 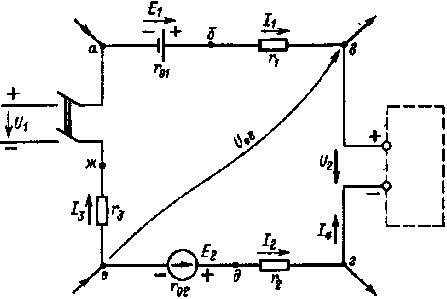 |
Пример 1.1. В замкнутом ковтуре рис. 1.3 Е1 = 100 В, Е2 = 50 В, U1 =120 В, U2 = 80 В, r01 = r02 = 1 Ом, r1 = 9 Ом, r2 = 4 Ом, r3 = 15 Ом, I1 = 2 А, I2 = 1 А, I4 = 3 А.
Определить ток I3 в ветви аже и напряжение Uев между точками е и в.
Решение. Выбрав положительное направление тока I3 таким, как показано на рис 1.3, и обходя контур по часовой стрелке, на основании второго закона Кирхгофа получим
E1 - Е2 = I1(r1 + r01) - I2(r2 + r02) + IЗr3 - U1 + U2.
После решения относительно тока I3 и подстановки числовых значений найдем I3 = 5 А. Так как ток I3 > 0, то он направлен, как показано на рис. 1.3.
При указанном на рис 1 3 положительном направлении напряжения Uеe по второму закону Кирхгофа для контура вгдев получим - Е2 = - I2(r2 + r02) +U2 + Uев. В результате вычислений найдем Uев = -125 В.
Поскольку Uев < 0, то φе < φв и действительное направление напряжения между точками е и в будет противоположным указанному на рисунке.
