ЭЛЕКТРОТЕХНИКА

Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

4.2. ПОДКЛЮЧЕНИЕ КАТУШКИ С r, L К СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ

Схема замещения реальной катушки (рис. 4,2, а)представляет собой последовательно соединенные резистивный r и индуктивный L элементы.

После включения выключателя (рис. 4.2, а) в цепи возникают ток и ЭДС самоиндукции. Уравнение для цепи, составленное по второму закону Кирхгофа, имеет вид

Выразив в уравнении е через

получим

Разделив почленно (4.5) на r, получим

L	di	+ i =	U	;
r	dt		r

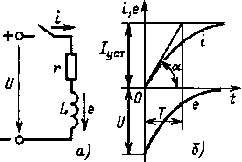Рис. 4.2. Зависимости i(t), e(t)(б) при подключении катушки r, L (а) к сети с постоянным напряжением

или где Т = L/r- электромагнитная постоянная времени, с.

В результате решения дифференциального уравнения (4.6) методом разделения переменных получим

Выражение (4.7) в показательной форме будет иметь вид

где A— постоянная интегрирования.

Постоянную интегрирования определяют на основании первого закона коммутации.
При t = 0 i(0+) = i(0-) = 0;

После подстановки в (4.8) значения А и решения его относительно i получим уравнение тока в цепи r, L

где Iуст = U/r — установившийся ток в цепи после окончания переходного процесса.

Подставив в (4.5) значение тока из (4.9), получим уравнение   ЭДС   самоиндукции   е,   возникающей   в   индуктивности:

На рис. 4.2, б изображены графики тока i(t)и ЭДС e(t)при включении цепи рис. 4.2, а.

Легко показать, что касательная, проведенная к кривой тока в начале координат, отсекает отрезок на линии установившегося значения тока, равный постоянной времени цепи Т. Действительно,  как   вытекает   извыражения   (4.5),   при   t = 0   и   i = 0

Из рис. 4.2, б

После подстановки получим

отсюда

Постоянная времени характеризует темп нарастания тока в цепи. Она зависит только от параметров цепи и позволяет без расчета и построения графиков оценить длительность переходного процесса.

Длительность переходного процесса, как видно из выражений (4.9) и (4,10), теоретически равна бесконечности. Практически же

Обычно считают, что длительность переходного процесса составляет

В практике расчетов переходных процессов в электрических цепях используют известный метод решения линейных дифференциальных уравнений с правой частью. Результат решения дифференциального уравнения равен сумме частного решения неоднородного дифференциального уравнения и общего однородного уравнения (когда правая часть исходного уравнения равна нулю). Для использования этого метода действительный (переходный) ток в ветви в соответствии с уравнением (4.9) представляют как сумму двух составляющих

где iуст - установившийся ток, т. е. ток, который устанавливается в цепи после окончания переходного процесса; iсв — свободный ток - ток, действующий только в течение времени переходного процесса.

Выразив в дифференциальном уравнении (4.5) ток через две составляющие, получим

Так как в установившемся режиме iсв = 0, то уравнение (4.13) приобретает вид

Ток в установившемся режиме есть величина постоянная, и его производная

diуст	= 0.
dt

Тогда из (4.14) следует, что

Вычитая (4.14) из (4.13), получим дифференциальное уравнение для свободного тока

Решением этого уравнения является выражение

где р — корень характеристического уравнения

Таким образом,

Действительный ток в цепи в переходном режиме

Значение А определяют из начальных условий: при t = 0 i(0+) = i(0-) = 0 и

Подставив значение A в (4.18), получим такое же уравнение для тока в цепи, как и при решении дифференциального уравнения методом разделения переменных:

i =	U	-	U	e-t/T = Iуст - Iуст e-t/T.
	r		r

Из изложенною вытекает, что установившийся ток определяется с помощью закона Ома, как в этом случае, или в разветвленных цепях с помощью законов Кирхгофа, а свободный - из решения исходного дифференциального уравнения без правой части.