Глава девятая
МАШИНЫ ПОСТОЯННОГО ТОКА
9.16. ЕСТЕСТВЕННЫЕ МЕХАНИЧЕСКИЕ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ
Одной из важнейших характеристик электродвигателей постоянного и переменного тока является механическая характеристика n(М), представляющая собой зависимость частоты вращения двигателя от развиваемого им момента. Учитывая, что при установившемся режиме работы момент двигателя равен моменту сопротивления на его валу (М = Мс), можно сказать, что механическая характеристика дает представление о характере и степени изменения частоты вращения двигателя от его механической нагрузки. Поскольку к характеру и степени изменения частоты вращения двигателя предъявляются со стороны различных производственных машин и механизмов разные требования, механические характеристики двигателей представляют большой практический интерес. Кроме механических характеристик значительный интерес представляют электромеханические характеристики. Применительно к двигателям постоянного тока — это зависимость частоты вращения от тока якоря n(Iя). Электромеханическая характеристика дает возможность производить ряд расчетов, связанных с выбором двигателя и других элементов его электрической цепи по нагреванию.
Механическая и электромеханическая характеристики считаются естественными, если к двигателю подведено напряжение, равное номинальному, а в цепи двигателя нет каких-либо дополнительных резистивных элементов.
Уравнение естественной электромеханической характеристики двигателей нетрудно получить из (9.18), решив его относительно частоты вращения и считая, что r = 0, rр = 0 и U = Uном :
| nе = | U - Iяrя | = | U | - | Iяrя | . |
| kеФ | kеФ | kеФ |
Заменив в (9.20) ток Iя согласно (9.9), получим уравнение естественной механической характеристики:
| nе = | U | - | Мrя | . |
| kеФ | kеkMФ2 |
Несмотря на то что уравнения (9.20) и (9.21) справедливы для всех двигателей постоянного тока, электромеханические и механические характеристики двигателей существенно отличаются друг от друга, что объясняется различным характером изменения магнитного потока.
Так как у двигателя постоянного возбуждения Ф = Фном = const, то электромеханическая и механическая характеристики двигателя прямолинейны (рис. 9.25, характеристики Ш). При работе двигателя вхолостую (М = Мс = 0 и Iя = 0) двигатель имеет частоту вращения холостого хода, которая определяется первым членом уравнения (9.20) или (9.21): n0ш = U/КеФ.
При увеличении нагрузки двигателя его частота вращения уменьшается за счет увеличения падения напряжения в сопротивлении rя. Изменение или перепад частоты вращения при какой-либо нагрузке определяется вторым членом уравнения (9.20) или (9.21):
| Δn = n0 - n = | Iяrя | - | Мrя | . |
| kеФ | kеkMФ2 |
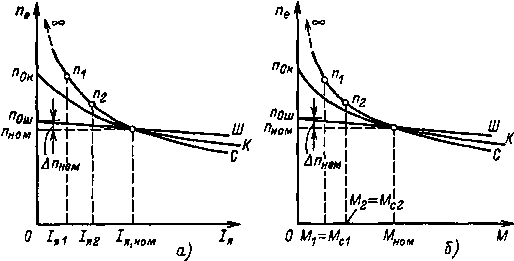 |
Рис. 9.25 Естественные электромехани- ческие (а) и механические (б) характеристики двигателей постоянного тока |
Изменение частоты вращения в процентах при переходе от холостого хода к номинальной нагрузке Δnном % = 100(n0ш - nпом)/n0ш для двигателей параллельного возбуждения мощностью от 5 до 100 кВт невелико и лежит в пределах примерно от 11 до 3,5% соответственно.
Учитывая небольшое изменение частоты вращения, говорят, что двигатель параллельного возбуждения имеет «жесткие» естественные электромеханическую и механическую характеристики, что является важнейшим его свойством.
Следует заметить, что вследствие реакции якоря естественные электромеханическая и механическая характеристики двигателя несколько отличаются от прямолинейных, а изменение частоты вращения несколько меньше, чем указано выше.
Одна из особенностей двигателя последовательного возбуждения состоит в том, что он не может работать вхолостую. Действительно, если М = Мс → 0, то I → 0 и Ф → 0. Как видно из (9.20) или (9.21), при этом n → ∞, т. е. частота вращения двигателя беспредельно увеличивается.
При увеличении нагрузки двигателя последовательного возбуждения возрастают падение напряжения в сопротивлении rя и магнитный поток. Как следует из (9.20), последнее приводит к дополнительному снижению частоты вращения. Поэтому электромеханическая и механическая характеристики двигателя последовательного возбуждения (рис. 9.25, характеристики С) получаются более «мягкими», чем у двигателя параллельного возбуждения. По мере насыщения магнитной цепи жесткость характеристик возрастает.
Двигатель смешанного возбуждения при работе вхолостую имеет магнитный поток Ф0 (см. рис. 9.23), которому соответствует частота вращения холостого хода n0к = U/kеФ0.
Обычно МДС параллельной обмотки выбирается так, чтобы получить n0к порядка 1,5 nном .
При увеличении нагрузки двигателя смешанного возбуждения его частота вращения уменьшается из-за увеличения магнитного потока и падения напряжения в сопротивлении якоря. Электромеханическая и механическая характеристики двигателя (рис. 9.25, характеристики К) получаются менее «жесткими», чем у двигателя параллельного возбуждения, у которого Ф = const, но более «жесткими», чем у двигателя последовательного возбуждения, у которого магнитный поток изменяется в более широких пределах (см. § 9.14).
При изменении нагрузки двигателей постоянного тока происходит следующее. Предположим, например, что двигатель последовательного возбуждения работал с моментом М1 = Мс1 и частотой вращения п1; моменту М1 соответствовал ток Iя1 (см рис. 9.25). Предположим далее, что момент статического сопротивления возрос и стал равен Мс2 > Мс1 . В первое мгновение после увеличения момента сопротивления из-за механической инерционности двигателя частота вращения не изменится и будет равна п1 . Вследствие этого не изменятся ЭДС Е1 , ток Iя1 и момент М1 двигателя. Поскольку Мс2 > М1, начнется переходный процесс, при котором частота вращения и ЭДС будут уменьшаться, а ток и момент будут возрастать. Установившийся режим наступит при частоте вращения n2, при которой наступит равенство М2 = Мс2.
Построение естественных характеристик двигателя параллельного возбуждения может быть произведено по уравнениям (9.20) и (9.21). Величину kеФ определяют обычно из (9.20), подставляя в него nе = nном и Iя = Iном .
Воспользоваться выражениями (9.20) и (9.21) для построения естественных характеристик двигателей последовательного и смешанного возбуждения не представляется возможным, так как магнитный поток этих двигателей не остается постоянным, а закон его изменения обычно не известен. Поэтому для указанных двигателей естественные электромеханические характеристики nе(I) приводятся в каталогах. Там же дается зависимость момента на валу от потребляемого тока: М(I). Имея nе(I) и М(I), нетрудно построить естественные механические характеристики nе(М).
В том случае, когда сведения о сопротивлении якоря отсутствуют, оно может быть определено приближенно из формулы (9.22), полученной на основании следующего соображения: при номинальной нагрузке двигателя потеря мощности в сопротивлении якоря составляет некоторую часть общих потерь мощности в двигателе, т. е.
| I2номrя ≈ α ( | Рном | - Рном) • 103, |
| ηном |
где Рном — номинальная (механическая) мощность двигателя, кВт; ηном — КПД двигателя при номинальной нагрузке; α — коэффициент, показывающий, какую часть общих потерь составляют потери мощности в сопротивлении якоря rя.
Обычно принимают: для двигателей параллельного возбуждения α = 0,5; для двигателей смешанного возбуждения α = 0,6; для двигателей последовательного возбуждения α = 0,75.
Пример 9.1 Двигатель параллельного возбуждения имеет следующие номинальные данные:
Uном = 220 В, Pном = 10 кВт, nном = 1100 об/мин, Iном = 53 А, ηном = 0,86.
Определить ЭДС якоря при номинальном режиме работы двигателя. Построить естественную механическую характеристику двигателя.
Решение Из формул (9.22) и (9.19), полагая r = 0, найдем
| rя = | α | ( | Pном | - Pном) • 103 ≈ 0,3 Ом, |
| I2ном | ηном |
Eном = U - Iном rя ≈ 204 В.
Из уравнения (9.20) при nном, Iном и уравнения (9.10) получим
| keФ = | Uном - Iном rя | = 0,185, kMФ = | КеФ | ≈ 1,76. |
| nном | 0,105 |
Уравнением естественной механической характеристики будет
| ne = | U | - | Мrя | = | 220 | - | М •0,3 | ≈ 1200 - 0,92 М. |
| kеФ | kеkMФ2 | 0,185 | 0,185•1,76 |
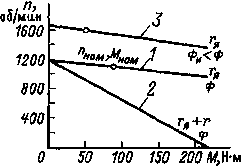 |
| Рис. 9.26. Механические характеристики двигателя параллельного возбуждения к примерам 9.1, 9.2 и 9.4 |
Для построения характеристики достаточно знать координаты ее двух точек. Например, при режиме холостого хода М = 0, nе = n0 = U/kеФ ≈ 1200 об/мин; при номинальном режиме n = nном= 1100 об/мин и
| Mном = | 9550Рном | = 87 Н • м. |
| nном |
Естественная механическая характеристика двигателя приведена на рис 9.26 (характеристика 1).
