Глава первая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1.10. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ОДНИМ ИСТОЧНИКОМ ЭНЕРГИИ И ПАССИВНЫМИ (РЕЗИСТИВНЫМИ) ЭЛЕМЕНТАМИ
Многие электрические цепи имеют лишь один источник энергии и то или иное число пассивных (резистивных) элементов. Это могут быть приемники электрической энергии и различные вспомогательные элементы.
Расчет и анализ неразветвленных и некоторых разветвленных цепей с одним источником и пассивными элементами производится с помощью закона Ома, первого и второго законов Кирхгофа, не требует совместного решения уравнений. Во многих случаях расчет и анализ осуществляются путем замены отдельных участков, а затем всей цепи одним элементом с эквивалентным сопротивлением и последующего перехода в процессе расчета к заданной цепи. В некоторых случаях целесообразно воспользоваться методом эквивалентного генератора (см. § 1.14).
1.10.1. Простейшая цепь с одним приемником. Допустим, что мы имеем простейшую неразветвленную электрическую цепь (рис. 1.4, а). В этой цепи участок amb представляет собой простейший пассивный двухполюсник, являющийся приемником электрической энергии, участок anb — простейший активный двухполюсник, являющийся источником.
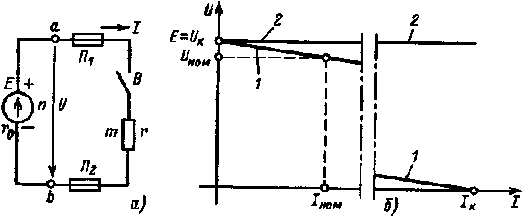 |
Рис. 1.4. Схема простейшей электрической цепи (а) и внешние характеристики источника (б) |
Необходимость изучения указанной цепи объясняется тем, что такие цепи часто встречаются на практике, а также тем, что к такой цепи могут быть сведены более сложные цепи, что облегчает их расчет и анализ.
Для рассматриваемой электрической цепи по второму закону Кирхгофа можно написать
Е = Ir0 + Ir;
E = Ir0 + U.
Из приведенных уравнений нетрудно получить формулу для определения тока и соотношение между напряжением и ЭДС источника:
I = E/(r0 + r) = E/rэ ;
U = Е - Ir0 ,
Как видно, при неизменных значениях ЭДС Е и внутреннего сопротивления r0 ток в цепи зависит от сопротивления r приемника. Напряжение источника U (равное в данной цепи напряжению приемника) меньше его ЭДС на падение напряжения I•r0 во внутреннем сопротивлении источника.
Если умножить (1.12) и (1.15) на ток, получим соотношения между мощностями
EI = I2r0 + I2r ;
UI = EI - I2r0 .
Правая часть (1.16) содержит потери мощности во внутреннем сопротивлении I2r0 и мощность, потребляемую приемником I2•r. Очевидно, произведение EI представляет собой мощность, вырабатываемую источником, т. е. электрическую мощность, преобразуемую им из другого вида мощности; например, если это генератор, — из механической мощности.
Если из вырабатываемой мощности вычесть потери мощности во внутреннем сопротивлении источника I2r0 , получим мощность UI, отдаваемую источником во внешнюю цепь, что нашло свое отражение в (1.17). Мощность, отдаваемая источником в данной цепи, равна мощности, потребляемой приемником, UI = I2r.
В связи с выражениями (116) и (1.17), а также схемой рис. 1.4, а необходимо обратить внимание на следующее. Вырабатываемая источником мощность определяется произведением тока на ЭДС, совпадающую по направлению с током, отдаваемая им мощность — произведением тока на напряжение, направленное внутри источника против тока; мощность, потребляемая приемником, определяется произведением тока на напряжение, совпадающее по направлению с током. Такие взаимные направления тока и ЭДС, а также тока и напряжения характерны для источников и приемников и в других электрических цепях. Учитывая это, выражения мощностей, вырабатываемых и отдаваемых источниками, а также потребляемых приемниками могут быть записаны следующим образом:
Pвыр = E I ;
Pотд = U I;
Pпотр = U I.
Выражения (1.19) и (1.20) справедливы также и для сколь угодно сложных активных двухполюсников, отдающих и потребляющих электрическую энергию.
Отношение мощности, отдаваемой источником, к вырабатываемой им мощности представляет собой КПД источника
| η = | Pотд | = | UI | = | U | = | r | . |
| Pвыр | EI | E | r0 + r |
Пользуясь полученными соотношениями, нетрудно установить, как будут меняться значения тока, напряжения, мощности и других величин при изменении сопротивления r, например, при подключении к источнику различных приемников или изменении числа параллельно включенных приемников. Если отключить приемник с помощью выключателя В (рис. 1.4, а),то электрическая цепь и все ее элементы будут работать в режиме холостого хода. В этом случае следует считать r = ∞. Из (1.14) видно, что при холостом ходе I = 0. Вследствие этого оказываются равными нулю падение напряжения Ir0, потери мощности I2r0 и мощности EI и UI. Так как
Ir0 = 0, то согласно (1.15) U = Ux = E.
Уменьшение сопротивления rприводит к увеличению тока I, падения напряжения Ir0, потерь мощности I2r0 и мощности EI. Напряжение U и КПД при этом уменьшаются.
Для того чтобы можно было судить о характере изменения мощности приемника, выразим ее следующим образом:
| Pпотр = I2r = Е2 | r | . |
| (r0 + r)2 |
Анализ выражения (1.22) показывает, что с уменьшением сопротивления r мощность Рпотр возрастает и при r = r0 достигает максимального значения. Дальнейшее уменьшение r приводит к уменьшению Рпотр . При r = 0 Рпотр = 0. Максимальное значение мощности Рпотр соответствует согласованному режиму работы приемника. Нетрудно установить, что при согласованном режиме U= 0,5Е, Рпотр = 0,5Pвыр , η = 0,5.
С технико-экономической точки зрения согласованный режим является нерациональным, так как к приемнику поступает лишь половина вырабатываемой источником мощности. Согласованный режим используется в некоторых радиотехнических устройствах, в автоматике и измерительной технике, когда важно получить максимальную мощность приемника. Энергетические соображения при этом не имеют решающего значения из-за малого абсолютного значения мощности.
В промышленных установках, где приходится иметь дело со значительными мощностями, важно, чтобы к приемнику поступала основная часть вырабатываемой мощности, а КПД имел большое значение. Это имеет место при r>>r0 .
Именно такое соотношение сопротивлений и характерно для номинального режима работы энергетических установок. Так как при номинальном режиме r>>r0 , то Uном = Iном r >> Iном r0 и согласно (1.15) напряжение источника будет мало отличаться от его ЭДС.
Если выводы приемника окажутся замкнутыми накоротко, например вследствие выхода из строя изоляции, то электрическая цепь будет работать в режиме короткого замыкания. В этом случае во всех соотношениях, полученных ранее, следует положить r = 0.
Так как при номинальном режиме r >> r0 , то номинальный ток I = Iном определяется в основном значением сопротивления r [см. (1.14)]. Поскольку при коротком замыкании r = 0, то
rэ = r0 и ток короткого замыкания оказывается намного больше номинального тока:
Iк = E/r0 >> Iн .
Естественно, что при коротком замыкании U = Iкr = 0 и Рпотр = UIк = 0. Мощность Рвыр = ЕIк значительно возрастет и целиком преобразуется в теплоту в сопротивлении r0. Последнее может привести к выходу из строя изоляции и даже к перегоранию проводов. В источнике, кроме того, наблюдается ряд других нежелательных явлений.
Простейшими аппаратами для защиты от возможных последствий коротких замыкании являются предохранители (П1 и П2 на рис. 1.4, а). Предохранитель имеет плавкую вставку, представляющую собой короткий проводник с меньшей термической стойкостью по сравнению с другими элементами цепи. При коротком замыкании плавкая вставка перегорает и отключает поврежденный участок цепи. Плавкие вставки изготовляются в большинстве случаев из медной проволоки и имеют настолько малое сопротивление, что практически не влияют на токи, напряжения и мощность в электрической цепи.
В дальнейшем предохранители на схемах изображаться не будут.
Одной из важнейших характеристик источников электрической энергии является их внешняя характеристика U(I). Внешняя характеристика показывает, как зависит напряжение источника от тока нагрузки, подчиняется уравнению (1.15), при Е = const и r0 = const представляет собой прямую линию (рис. 1.4,б, характеристика 1). На характеристике показаны точки, соответствующие режимам холостого хода, короткого замыкания и номинальному режиму работы источника.
Из соотношения (1.15) следует, что напряжение источника можно считать постоянным и равным его ЭДС (U = E = const), если пренебречь внутренним сопротивлением r0 источника. В этом случае источник называют идеальным источником ЭДС. Внешняя характеристика идеального источника приведена на рис. 1.4,б (характеристика 2).
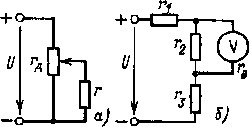
1.10.2. Электрические цепи с последовательным соединением резистивных элементов. Последовательным называется такое соединение элементов, когда условный конец первого элемента соединяется с условным началом второго, конец второго — с началом третьего и т. д. Характерным для последовательного соединения является один и тот же ток во всех элементах. Последовательное соединение нашло широкое применение на практике. Например, последовательно с приемником r часто включается резистор rр для регулирования напряжения, тока или мощности приемника (рис. 1.5,а). Для расширения пределов измерения вольтметров последовательно с ними включают добавочные резисторы rд (рис. 1,5, б). С помощью реостата, включаемого последовательно в различные ветви цепи двигателя постоянного тока, производят изменение его пускового тока или частоты вращения.
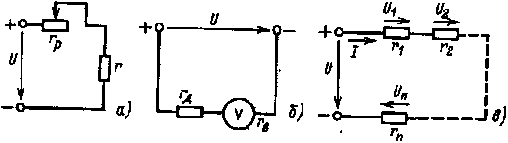 |
Рис. 1.5. Схема электрических цепей с последовательным соединением резистивных элементов |
В общем случае при последовательном соединении и резистивных элементов (рис. 1.5, в) ток в цепи, напряжения на элементах и потребляемые ими мощности определяются следующими соотношениями:
| n | ||
| I = U/ | ∑ | rk = U/rэ , Uk = Irk , Pk = IUk = I2rk ., |
| 1 |
Напряжение и мощность всей цепи
| n | n | n | n | n | ||||||
| U = | ∑ | Uk = I | ∑ | rk , P = | ∑ | Pk = IU = I | ∑ | Uk = I2 | ∑ | rk. |
| 1 | 1 | 1 | 1 | 1 |
Соотношение между напряжениями, мощностями и сопротивлениями элементов
Uk /Ul = Pk /Pl = rk /rl ,
С помощью приведенных формул нетрудно выяснить характер изменения тока, напряжений и мощностей при изменении значений сопротивлений или числа включенных резистивных элементов. Например, если увеличить число элементов, то эквивалентное сопротивление возрастает, а ток, напряжения и мощности ранее включенных элементов уменьшаются; уменьшается также и общая мощность.
Приемники электрической энергии последовательно, как правило, не соединяются, так как при этом требуется согласование номинальных данных приемников, исключается возможность независимого их включения и отключения, а при выходе из строя одного из приемников отключаются также остальные приемники. Чаще их включают параллельно.
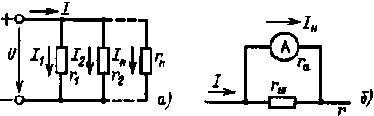 |
| Рис. 1.6. Схемы электрических цепей с параллельным соединением резистивных элементов |
1.10.3. Электрические цепи с параллельным соединением резистивных элементов.
Параллельным называется такое соединение резистивных элементов, при котором соединяются между собой как условные начала всех элементов, так и их концы (рис. 1.6, а). Характерным для параллельного соединения является одно и то же напряжение U на выводах всех элементов. Параллельно соединяются обычно различные приемники электрической энергии и другие элементы электрических цепей, рассчитанные на одно и то же напряжение. При параллельном соединении не требуется согласовывать номинальные данные приемников, возможно включение и отключение любых приемников независимо от остальных, а при выходе из строя какого-либо приемника остальные остаются включенными.
Параллельное соединение применяется часто для расширения пределов измерения амперметров (рис. 1.6,б): если ток I в электрической цепи превышает номинальный ток Iном амперметра, параллельно с ним включают шунтирующий резистор rш . Нередко параллельное соединение используют для уменьшения эквивалентного сопротивления какого-либо участка электрической цепи.
Токи и мощности параллельно соединенных ветвей (рис. 1.6, а) при U = const не зависят друг от друга и определяются по формулам
Ik = U/rk = Ugk ; Pk = UIk = U2/rk = U2gk = Ik2rk .
| n | n | n | ||||
| I = | ∑ | Ik = U | ∑ | 1/rk = U | ∑ | gk =Ugэ = U/rэ ; |
| 1 | 1 | 1 |
| n | n | |||
| Pk = | ∑ | Pk = UI = U | ∑ | Ik = U2gэ = U2/rэ = I2rэ , |
| 1 | 1 |
| n | ||
| где gэ = | ∑ | gk— эквивалентная проводимость; rэ = 1/gэ— эквивалентное сопротивление. |
| 1 |
Соотношения между токами, мощностями, проводимостями и сопротивлениями:
Ik /Il = Pk /Pl = gk /gl = rl /rk .
При увеличении числа параллельно соединенных ветвей эквивалентная проводимость электрической цепи возрастает, а эквивалентное сопротивление соответственно уменьшается. Это приводит к увеличению тока I. Если напряжение остается постоянным, то увеличивается также общая мощность Р; токи и мощности ранее включенных ветвей не изменяются.
1.10.4. Электрические цепи со смешанным соединением резистивных элементов. Смешанным, или последовательно-параллельным, называется такое соединение резистивных элементов, при котором на одних участках электрической цепи они соединены параллельно, а на других последовательно.
Смешанное соединение имеет место, например, при питании приемников с сопротивлениями r1 и r2 по проводам электрической сети с сопротивлениями rл (рис. 1.7, а), при регулировании напряжения приемника r с помощью делителя напряжения (потенциометра) rд (рис. 1.8, а), в случае измерения вольтметром напряжения на одном из резисторов (рис. 1.8, б).
Анализ и расчет электрических цепей со смешанным соединением резистивных элементов производится чаще всего путем предварительных их преобразований. Рассмотрим в качестве примера последовательность расчета электрической цепи, изображенной на рис. 1.7, а.
Пример 1.2. В электрической цепи рис. 1.7,a U = 115 В, r1= 20 Ом, r2 = 30 Ом, rл = 0,5 Ом.
Определить токи, напряжение Uab приемников, мощности приемников, потери напряжения и мощности в проводах, мощность, потребляемую от источника.
Решение. Электрическая цепь рис. 1.7,а может быть заменена цепями, изображенными на рис. 1.7,б и в, в которых
| rэ1 = | r1r2 | = 12 Ом, rэ = rэ1 + 2rл = 13 Ом. |
| r1 + r2 |
Используя электрическую цепь, изображенную на рис. 1.7,в, определим ток I, а перейдя к цепям рис. 1.7, а и б, найдем напряжение Uab и токи I1 и I2 :
I1 = Uab/r1 ≈ 5,31 А; I2 = Uab /r2 ≈ 3,54 А
Мощности приемников и мощность, потребляемая из сети,
P1 = Uab I1≈ 564 Вт, Р2 = Uab I2 ≈ 376 Вт,
Р = UI ≈ 1018 Вт.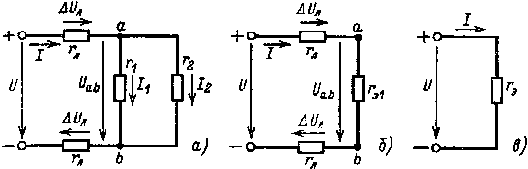 |
Рис. 1.7. Схема электрической цепи (а) к примеру 1.2 и схемы эквивалентных ей цепей (б и в) |
 |
| Рис. 1.8 Примеры электрических цепей со смешанным соединением резистивных элементов |
Потери напряжения и мощности в проводах
2Iлrл = 8,85 В, 2Iл2rл ≈ 78 Вт.
Используя соотношения, полученные в примере 1.2, нетрудно сделать следующие важные выводы в отношении характера изменения различных величин при смешанном соединении резистивных элементов. С увеличением числа приемников в электрической цепи (см. рис. 1.7, а) сопротивления rэ1 и rэ уменьшатся. Это приведет к увеличению тока I, мощности Р, потерь напряжения 2Irл и мощности 2I2rл . Из-за увеличения потерь напряжения в проводах снизится напряжение Uab и как следствие этого уменьшатся токи I1 и I2, а также мощности P1 и Р2.
Чтобы напряжение приемников незначительно колебалось при изменении их числа или режима работы и было близким к номинальному, площадь поперечного сечения S проводов рассчитывают по допустимой потере напряжения ΔU при номинальном режиме из формулы
| ΔU% = | 2Irл | 100 = | 2Iρl | 100. |
| Uном | UномS |
В электрических цепях различного назначения допустимая потеря напряжения лежит примерно в пределах 2 — 6%.
Из двух сечений проводов, определенных по нагреванию и допустимой потере напряжения, выбирают большее.
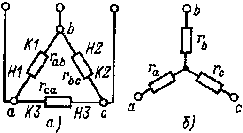 |
| Рис. 1.9. Схема соединения резистивных элементов треугольником (а) и звездой (б) |
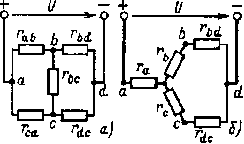 |
| Рис. 1.10. Схема мостовой цепи (а) и соответствующая ей схема после замены одного из треугольников звездой (б) |
1.10.5. Электрические цепи, содержащие соединения резистивных элементов треугольником. Под соединением треугольником (рис. 1.9,а) понимается такое, при котором вывод К1 одного из элементов соединяется с выводом Н2 второго, вывод К2 второго - с выводом Н3 третьего, а вывод К3 третьего — с выводом H1 первого элемента. Узловые точки a, b и с подключаются к остальной части электрической цепи.
Для упрощения анализа и расчета некоторых электрических цепей, содержащих соединения резистивных элементов треугольником, целесообразно заменить их эквивалентными резистивными элементами, соединенными звездой (рис. 1.9,б). Примером подобных электрических цепей являются мостовые цепи (рис. 1.10, а). Как видно, в мостовой цепи резистивные элементы образуют два смежных треугольника (rab, rbc, rcaиrbc, rbd, rdc) и нет ни одного элемента, который был бы соединен с другими последовательно или параллельно. Это осложняет расчет и анализ электрической цепи. Однако если заменить, например, резистивные элементы rab , rbc и
rса , соединенные треугольником, эквивалентными элементами ra , rb и rс , соединенными звездой (рис. 1.10,б), то получим цепь со смешанным соединением резистивных элементов, методика расчета которой была рассмотрена выше.
Замена треугольника резистивных элементов эквивалентной звездой должна производиться таким образом, чтобы после указанной замены токи в остальной части цепи, а также напряжения между точками ab, be и са остались без изменения.
С помощью законов Кирхгофа можно получить следующие формулы для определения сопротивлений эквивалентной звезды:
| ra = | rab rса | = | rab rсa | ; rb = | rabrbc | , rс = | rса rbc |
| rab + rbc + rса | ΣrΔ | ΣrΔ | ΣrΔ |
Иногда оказывается целесообразным заменить резистивные элементы, соединенные звездой, эквивалентным треугольником. Соответствующие формулы можно получить путем совместного решения выражений (1.23).
Следует заметить, что для расчета мостовых цепей часто используется метод эквивалентного генератора (см. § 1.14 и пример 1.4).
