Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.10. ЭЛЕКТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕХАНИЧЕСКИХ И ДРУГИХ СИСТЕМ
Разработка новых сложных механических, гидравлических и других систем связана со значительными трудностями, состоящими в том, что нет гарантии получения требуемых расчетных величин и нет возможности провести экспериментальные исследования системы, поскольку она не выполнена в натуре. Поэтому при разработке той или иной системы прибегают к созданию физической модели системы. Результаты исследования модели позволяют выявить действительные характеристики и дать рекомендации для корректировки параметров системы с целью получения оптимальных характеристик. Наиболее простыми и универсальными моделями для исследования как стационарных, так и переходных режимов механических и других систем являются электрические модели, представляющие собой электрические цепи с резистивными, емкостными и индуктивными элементами, в которых аналогами исследуемых величин являются ток, напряжение, индуктивность и емкость. Выполнение электрической модели и проведение ее исследования не связано скакими-либо техническими трудностями и не требует значительных затрат. Создание же механической модели связано со значительными трудностями и капитальными затратами.
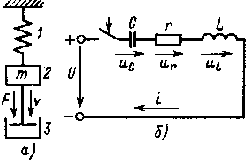 |
| Рис. 4.10. Механическая система (а) и ее электрическая модель (б) |
Электрическая модель будет соответствовать реальной системе, если математическое описание модели и системы одинаковое.
Рассмотрим электрическую модель механической системы, изображенной на рис. 4.10, а. Механическая система состоит из тела 2 с массой т, пружины 1 и воздушного демпфера 3, состоящего из поршня, расположенною в цилиндре. Допустим, тело 2 удерживалось в неподвижном состоянии внешней силой, когда пружина 1 была ненапряженной. После удаления внешней силы под действием силы тяжести система придет в движение. Тело начнет опускаться, пружина — растягиваться, появится демпфирующая сила демпфера. Возникнет переходный процесс, который постепенно затухнет и система снова окажется в неподвижном состоянии. Электрической моделью рассмотренной механической системы является электрическая цепь с резистивным, индуктивным и емкостным элементами, изображенная на рис. 4.10, б, так как дифференциальное уравнение переходного процесса этой цепи при подключении ее к источнику с постоянным напряжением аналогично дифференциальному уравнению переходного процесса механической системы.
Уравнение движения механической системы имеет вид
F - F1 - F2 = m dv/dt,
где F — сила тяжести массы; F1 = k1x- упругая сила пружины; F2 = k2v — сила, развиваемая демпфером; х - перемещение тела от начального положения; v — скорость тела. Таким образом, для механической системы
F = k1x + k2v + m dv/dt.
Уравнение переходного процесса электрической цепи
U = uC + ur + uL = 1/C ∫ i dt + ir + L di/dt.
Из сравнения уравнений (4.57) и (4.58) следует, что напряжение U, приложенное к цепи, является аналогом силы F, приложенной к механической системе, напряжение uC на емкости —аналогом силы, развиваемой пружиной, ток i цепи — аналогом скорости u, ur — аналогом силы, возникающей в демпфере, индуктивность L — аналогом массы мела m.
Таким образом, благодаря единству уравнений электрической цепи и механической системы исследование явлений в механической системе может быть произведено с помощью исследования переходных процессов электрической цепи. Характер переходного процесса механической системы, так же как и ее электрической модели, может быть апериодическим или колебательным. В механической системе он определяется соотношением массы тела, упругости пружины и демпфирующей силы демпфера, в электрической модели, как это доказано в § 4.9, — соотношением параметров цепи r, L, С.
Результаты решения уравнения электрической цепи будут отображать характер и длительность переходного процесса механической системы, если соблюдены соответствующие соотношения между параметрами механической системы и ее моделью — электрической цепью. Соотношения устанавливаются посредством масштабных коэффициентов. Значения и размерность масштабных коэффициентов можно установить, если разделить почленно уравнение (4.58) на уравнение (4.57).
В результате получим
| [ | U | = [mF] В/Н; | [ | uC | = [mF] В/Н; |
| F | k1x |
| [ | ri | = [mk2mv ] Ом • м/(Н • c) • A • c/м = B/H; |
| k2v |
| [ | Ldi/dt | ] = [ | L | di/dt | ] | = [mmmdv/dt]Гн • м/(Н • с) • А • с2/(с • м) = В/Н. | |
| m dv/dt | m | dv/dt |
Выразив в уравнении (4.57) соответствующие величины через масштабные коэффициенты, получим уравнение электрической цени с учетом масштабных коэффициентов
| U | = | uC | + | ri | + | Ldi/dt | . |
| mF | mF | mk2mv | mmmdv/dt |
