ЭЛЕКТРОТЕХНИКА

Глава третья
ТРЕХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

3.4. СОЕДИНЕНИЕ ПРИЕМНИКОВ ЗВЕЗДОЙ

Как видно из схемы рис. 3.7, при соединении звездой фазные напряжения приемника Ua, Ub и Uc не равны линейным напряжениям Uab, Ubc и Uca. Применяя второй закон Кирхгофа и к контурам aNba, bNcb и cNac, можно получить следующие соотношения между  линейными  и  фазными  напряжениями:

Пользуясь соотношениями (3.7) и имея векторы фазных напряжений, нетрудно построить векторы линейных напряжений (рис. 3.8).

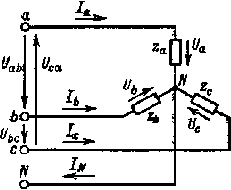Рис. 3.7. Схема соединения фаз приемника звездой

Если не учитывать сопротивлений линейных проводов и нейтрального провода, то следует считать комплексные значения линейных и фазных напряжений приемника равными соответственно комплексным значениям линейных и фазных напряжений источника. Вследствие указанного равенства векторная диаграмма напряжений приемника не отличается от векторной диаграммы источника при соединении звездой (см. рис. 3.5, б и 3.8). Линейные и фазные напряжения приемника, как и источника, образуют две симметричные системы  напряжений. Очевидно, между линейными и фазными напряжениями приемника существует соотношение, подобное (3.6), т. е.

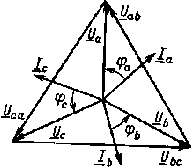Рис. 3.8. Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки

Как будет показано далее, соотношение (3.9) справедливо при определенных условиях так же в случае отсутствия нейтрального провода, т. е. в трехпроводной цепи.

На основании указанного соотношения можно сделать вывод о том, что соединение звездой следует применять в том случае, когда каждая фаза трехфазного приемника или однофазные приемники рассчитаны на напряжение в √3 раз меньшее, чем номинальное линейное напряжение сети.

Из схемы рис. 3.7 видно, что при соединении звездой линейные токи равны соответствующим фазным токам:

С помощью первого закона Кирхгофа получим следующее соотношение между фазными токами и током нейтрального провода:

Имея векторы фазных токов, с помощью (3.11) нетрудно построить вектор тока нейтрального провода.

Если нейтральный провод отсутствует, то, очевидно,

3.4.1. Симметричная нагрузка. Нагрузка считается симметричной, когда равны в отдельности активные и реактивные сопротивления всех фаз:

где ха = хLа - хCа и т. д.

Условие симметричности нагрузки может быть  записано также через комплексные значения полных сопротивлений фаз: Za = Zb = Zc .

Симметричная нагрузка трехфазной цепи возникает при подключении к сети трехфазных приемников (см. § 3.1).

Будем считать сначала, что при симметричной нагрузке имеется нейтральный провод.

В отношении любой фазы справедливы все формулы, полученные ранее для однофазных цепей. Например, для фазы a

Так как в четырехпроводной цепи Ua = Ub = Uc = Uф = Uл /√3, то, очевидно, при симметричной нагрузке

Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена на рис. 3.8.

Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе IN = Ia + Ib + Ic = 0.

Очевидно, отключение нейтральною провода при IN = 0 не приведет к изменению фазных напряжений, токов, углов сдвига фаз, мощностей и векторной диаграммы. Даже при отсутствии нейтрального провода фазные напряжения оказываются равными Uф = Uл /√3, т. е. тому напряжению, па которое рассчитаны фазы трехфазного приемника.

Из сказанного следует, что при симметричной нагрузке в нейтральном проводе нет необходимости и при симметричной нагрузке нейтральный провод не применяется.

Мощности трехфазного приемника могут быть выражены так:

В качестве номинальных напряжений и токов трехфазных приемников указываются обычно линейные напряжения и токи. Учитывая это, мощности трехфазных приемников целесообразно также выражать через линейные напряжения и токи. Заменив в (3.13) фазные напряжения и   ток согласно (3.8) и (3.9), получим

Пример 3.1. К трехфазной сети с линейным напряжением Uл = Uab = Ubc = Uca = 380 В должен быть подключен трехфазный приемник, каждая фаза которого рассчитана на напряжение 220 В и имеет активное сопротивление rф = 10 Ом, а также индуктивное сопротивление xф = 10 Ом, соединенные последовательно.

Определить фазные токи, углы сдвига фаз между фазными напря­жениями и токами, а также мощности.

Решение. Так как каждая из фаз приемника рассчитана на напряжение, в √3 раз меньшее номинального напряжения сети, то приемник должен быть соединен звездой (см. рис. 3.7). Поскольку нагрузка симметричная, нейтральный провод подводить к приемнику не следует.

Полные сопротивления фаз, фазные токи и углы сдвига фаз между фазными напряжениями и токами

zф = √rф2 + xф2 ≈ 14,1 Ом;    Iф = Uф /zф =	Uл	≈ 15,6 А,
	√3zф

φф = arcsin	xф	= 45°.
	zф

Полная, активная и реактивная мощности  приемника и любой фазы

Р = S соs φф = S	rф	≈7270 Вт = 7,27 кВт,
	zф

Q = S sin φф = S	x	≈ 7270 вар = 7,27 квар;
	zф

Q -	Q	≈ 2426 вар ≈ 2,43 квар.
	3

Векторная диаграмма приемника приведена на рис. 3.8.

3.4.2. Несимметричная нагрузка. Нагрузка считается несимметричной, когда сопротивление хотя бы одной из фаз не равно сопротивлениям других фаз. Например, нагрузка будет несимметричной, если ra = rb = rc , ха = хb ≠ хc . В общем случае при несимметричной нагрузке является полное отключение одной или двух фаз.

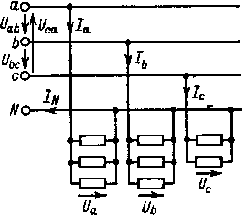Рис. 3.9. К вопросу о соединении однофазных приемников звездой

Несимметричная нагрузка возникает обычно при подключении к трехфазной сети однофазных приемников (см. § 3.1). Последние могут иметь различные мощности, могут располагаться территориально в разных местах (в различных помещениях, на разных этажах и т. д.), могут включаться и отключаться независимо друг от друга.

Когда имеется несколько однофазных приемников, для бо­лее равномерной загрузки линейных проводов сети их делят на три примерно одинаковые в отношении мощности группы (рис. 3.9), называемые фазами приемников. Одни выводы приемников различных фаз подключают к трем различным линейным проводам сети, а другие выводы приемников всех фаз — к нейтральному проводу. Так как все приемники рассчитаны на одно и то же напряжение, то в пределах каждой фазы они соединяются параллельно.

Если в пределах каждой фазы приемники заменить одним приемником с эквивалентным сопротивлением и расположить их соответствующим образом, получим схему, приведенную на рис. 3.7.

Особенностью электрической цепи при несимметричной нагрузке является то, что она должна иметь обязательно нейтральный провод. Объясняется это тем, что при его отсутствии значения фазных напряжений приемников существенно зависят от степени несимметрии нагрузки, т. е. от значений и характера сопротивлений приемников различных фаз. Поскольку последние могут изменяться в широких пределах при изменении числа включенных приемников, существенно могут изменяться и фазные напряжения. На одних приемниках напряжение может оказаться значительно больше, а на других — меньше фазного напряжения сети Uл /√3, т. е. того напряжения, на которое рассчитаны приемники. А это недопустимо.

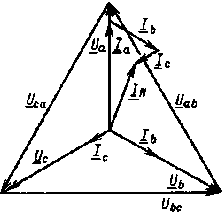Рис. 3.10. Векторная диаграмма при соединении приемников звездой в случае несимметричной нагрузки и при наличии нейтрального провода

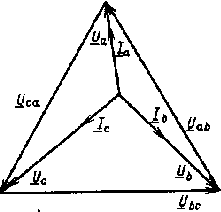Рис. 3.11. Векторная диаграмма при соединении приемников звездой в случае несимметричной нагрузки и обрыве нейтрального провода

Для иллюстрации сказанного на рис. 3.10 приведена векторная диаграмма цепи рис. 3.7 с несимметричной активной нагрузкой фаз при наличии нейтрального провода, а на рис. 3.11 — диаграмма той же цепи при его обрыве. Из сравнения диаграмм отчетливо видны последствия обрыва нейтрального провода.

Необходимость нейтрального провода становится особенно очевидной, если представить себе, что при отсутствии нейтрального провода отключили все приемники, например, фаз а и b. Очевидно, напряжение фазы с при этом окажется равным нулю, так как фаза с окажется также отключенной. Если вообразить, что имеется всего лишь один однофазный приемник, рассчитанный на напряжение Uл /√3, то при отсутствии нейтрального провода его попросту было бы некуда включить.

Для повышения надежности соединения приемников с источником с помощью нейтрального провода в цепи последнего не ставят выключателей и даже защитных устройств, например предохранителей.

Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также фазные мощности при несимметричной нагрузке в цепи с нейтральным проводом будут в общем случае различными. Все они могут быть определены по приведенным ранее формулам (3.12). Для определения мощностей всех фаз следует воспользоваться выражениями

Очевидно, формулы (3.13) и (3.14) не пригодны для определения мощностей при несимметричной нагрузке.

Если требуется определить ток IN нейтрального провода, то следует решать задачу комплексным методом. Можно также определить ток IN по векторной диаграмме, которая, естественно, должна быть построена в масштабе.

При решении задачи в комплексной форме необходимо прежде всего выразить в комплексной форме полные сопротивления фаз и фазные напряжения. После этого нетрудно найти комплексные выражения фазных токов. Например, комплексное выражение тока Ia будет равно Ia = Ua /Za .

Комплексное значение тока в нейтральном проводе определяют по формуле (3.10).

Комплексным методом можно воспользоваться и для определения фазных мощностей. Так, мощности фазы а будут равны

Пример 3.2. В электрической цепи рис. 3.7 линейные напряжения Uл = 220 В. В фазе а включено параллельно 20 ламп, в фазе b— 10 ламп, в фазе С — 5 ламп. Номинальное напряжение и мощность каждой лампы равны Uном = 127 В, Рном = 100 Вт. Определить фазные токи, ток каждой лампы и ток нейтрального провода.

Решение. Учитывая, что лампы имеют только активное сопротивление, из формулы мощности найдем номинальный ток лампы, а по закону Ома - сопротивление лампы:

Зная сопротивление лампы и числи ламп в каждой фазе, нетрудно определить сопротивление фаз, а затем фазные токи:

Так как при Uл = 220 В напряжение на лампах равно их номинальному напряжению, т. е. 127 В, то каждая лампа будет потреблять ток. равный номинальному, т. е. 0,79 А.

Для определении тока в нейтральном проводе решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные значения фазных напряжений приемника равны комплексным значениям соответствующих ЭДС [см. (3.2)], то

Комплексные значения фазных сопротивлений: Za = 8,05 Ом, Zb = 16,1 Ом, Zc = 32,2 Ом.

Комплексные значения токов и действующее значение тока нейтрального провода:

Векторная диаграмма к примеру 3.2 дана на рис. 3.10.