Глава первая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1.16. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1.16.1. Нелинейные элементы электрических цепей, их вольт-амперные характеристики и сопротивления. Нелинейным элементом электрической цепи считается элемент, значения параметров которого зависят от значения тока данного элемента или напряжения на его выводах.
К нелинейным элементам электрических целей относятся разнообразные электронные, полупроводниковые и ионные приборы, устройства, содержащие намагничивающие обмотки с ферромагнитными магнитопроводами (при переменном токе), лампы накаливания, электрическая дуга и др.
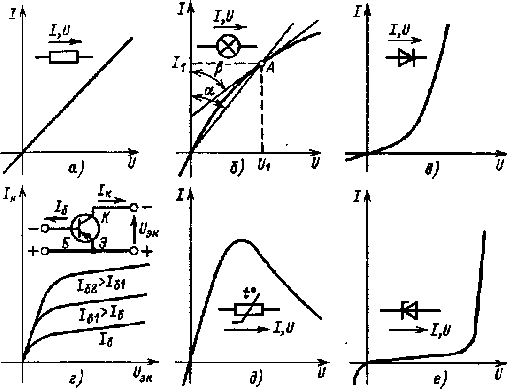 |
Рис. 1.21. Примеры вольт-амперных характеристик: а — линейного элемента; б — лампы накаливания; в - полупроводнико- вого диода; г - транзистора (при различных токах базы), д - терморезистора, е - стабилитрона |
Нелинейные элементы получают в настоящее время все более широкое распространение, так как они дают возможность решать многие технические задачи. Так, с помощью нелинейных элементов можно осуществить преобразование переменного тока в постоянный, усиление электрических сигналов, генерирование электрических сигналов различной формы, стабилизацию тока и напряжения, изменение формы анналов, вычислительные операции и т д. Нелинейные элементы широко используются в радиотехнических устройствах, в устройствах промышленной электроники, автоматики, измерительной и вычислительной техники.
Важнейшей характеристикой нелинейных элементов является вольт-амперная характеристика (в. а. х.), представляющая собой зависимость между током нелинейного элемента и напряжением на его выводах: I(U) или U(I).
Зависимость между током I и напряжением U любого пассивного элемента электрической цепи подчиняется закону Ома, согласно которому I = U/r. Поскольку у линейных элементов с изменением тока или напряжения сопротивление остается постоянным, их в. а. х. не отличаются от прямой (рис. 1.21, а).
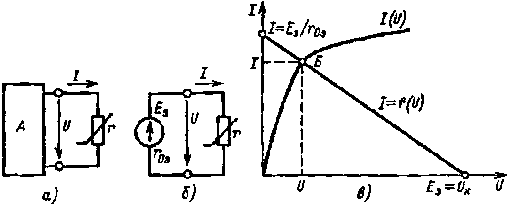 |
Рис. 1.22, К расчету электрической цепи с нелинейным элементом графо- аналитическим методом |
У нелинейных элементов в. а. х. весьма разнообразны и для некоторых из них даны на рис. 1.21,б — е. Там же приведены условные графические обозначения соответствующих элементов. Общее условное обозначение любого нелинейного резистивного элемента показано на рис. 1.22, а.
Имея в. а. х. нелинейного элемента, можно определить его сопротивления при любых значениях тока или напряжения. Различают два вида сопротивлений нелинейных элементов: статическое и дифференциальное.
Статическое сопротивление дает представление о соотношении конечных значений напряжения и тока нелинейного элемента и определяется в соответствии с законом Ома. Например, для точки А в. а. х. (рис. 1.21,б) статическое сопротивление
| rs = | U1 | = | mu | tg α, |
| I1 | mi |
Дифференциальное сопротивление позволяет судить о соотношении приращений напряжения и тока и определяется следующим образом:
| rd = | dU1 | = | mu | tg β, |
| dI1 | mi |
К нелинейным электрическим цепям применимы основные законы электрических цепей, т. е. закон Ома и законы Кирхгофа. Однако расчет нелинейных цепей значительно труднее, чем линейных, Объясняется это тем, что кроме токов и напряжений, подлежащих обычно определению, неизвестными являются также зависящие от них сопротивления нелинейных элементов.
Для расчета нелинейных электрических цепей применяется с большинстве случаев графоаналитический метод. Однако если в предполагаемом диапазоне изменения тока или напряжения нелинейного элемента его в. а. х. можно заменить прямой линией, то расчет можно производить и аналитическим методом.
Следует отметить, что к той части электрической цепи, которая содержит линейные элементы, применимы все методы расчета и преобразования электрических цепей, рассмотренные ранее.
1.16.2. Графоаналитический метод расчета нелинейных электрических цепей. Предположим, что имеется электрическая цепь, схема которой приведена на рис. 1.22, а. В этой цепи нелинейный резистивный элемент r соединен с активным линейным двухполюсником А, который может быть любой сложности.
Расчет данной электрической цепи следует начать с замены активного двухполюсника эквивалентным генератором с параметрами Еэ = Ux и r0э (рис. 1.22,б) согласно методу эквивалентного генератора. Для дальнейшего расчета целесообразно воспользоваться методом графического решения двух уравнений с двумя неизвестными. Одним из уравнений следует считать зависимость I(U) нелинейного элемента, которой соответствует его в. а. х., приведенная на рис. 1.22, в. Другое уравнение, связывающее те же ток I и напряжение U, нетрудно получить по второму закону Кирхгофа. Применив его к цепи с эквивалентным генератором (рис. 1.22,б), получим
| I = | Еэ - U | = f(U). |
| r0э |
Поскольку зависимость I = f(U) линейная, график I = f(U) может быть построен по двум точкам (рис. 1.22,в). Например; в режиме холостого хода эквивалентного генератора I = 0 и U = Ux = Еэ; в режиме короткого замыкания U = 0 и I = Iк = Еэ /r0э .
Очевидно, искомые ток I и напряжение U определяются точкой Б пересечения в. а. х. I (U) нелинейного элемента и графика I = f(U) эквивалентного генератора.
Если к двухполюснику будут подключены два нелинейных элемента r1 и r2, соединенные последовательно (рис 1.23, а), то перед расчетом согласно методике, изложенной выше, необходимо заменить их эквивалентным нелинейным элементом rэ (рис 1.23, б) с эквивалентной в. а. х. I (U) (рис. 1.23, в). Построение эквивалентной в. а. х. I(U) производили на основании следующего соображения: при любом значении тока I напряжение U равно сумме напряжений U1 и U2 нелинейных элементов (рис. 1.23, а), т. е.
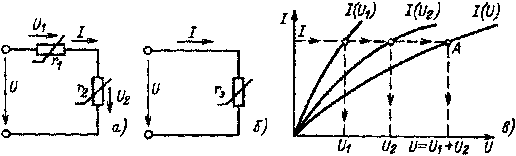 |
Рис. 1.23. К построению в.а.х. электри- ческой цепи при последова- тельном соединении нелинейных элементов |
U = U1 + U2.
Задавшись несколькими значениями тока I, по в. а. х. I(U1)и I(U2) нелинейных элементов r1 и r2 находят соответствующие напряжения U1 и U2, после чего согласно выражению (1.42) определяют напряжение U и строят в. а. х. I(U).
На рис. 1.23, в показано в качестве примера определение при токе I напряжения Uодной из точек (А) в. а. х. I(U).
Когда двухполюсник представляет собой источник с заданным напряжением, после построения в. а. х. I(U) можно при любом напряжении U найти ток I, а затем с помощью в. а. х. I(U1) и I(U2) — напряжения U1 и U2.
При параллельном соединении двух нелинейных элементов (рис. 1.24) для построения в. а. х. I(U)эквивалентного нелинейного элемента rэ (рис. 1.25) необходимо воспользоваться тем, что при любом значении напряжения U токи связаны соотношением
I = I1 + I2.
Задавшись несколькими значениями напряжения U, по в. а. х. I1(U) и I2(U) (рис. 1.25) нелинейных элементов r1 и r2 находят соответствующие токи I1 и I2, после чего согласно (1.43) определяют ток I и строят в. а. х. I(U).
При смешанном соединении нелинейных элементов следует сначала построить ВАХ участка с параллельным соединением элементов. После этого можно перейти к построению ВАХ всей цепи. Имея в распоряжении все ВАХ, нетрудно определять токи и напряжения всех элементов цени.
1.16.3. Аналитический метод расчета нелинейных электрических цепей. Предположим, что имеется некоторый нелинейный элемент, в. а. х. которого приведена на рис. 1.26, а. Если данный элемент должен работать на линейном участке cd в. а. х., то для расчета и анализа можно использовать аналитический метод.
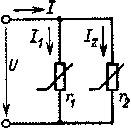 |
| Рис. 1.24. Параллельное соединение нелинейных элементов |
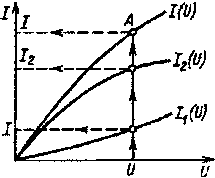 |
| Рис. 1.25. К построению в. а. х. электрической цепи при параллельном соединении нелинейных элементов |
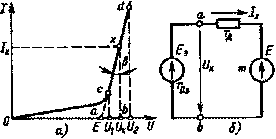 |
| Рис. 1.26. К расчету электрической цепи с нелинейным элементом аналитическим методом |
Чтобы выяснить зависимость между напряжением и током участка cd и построить схему замещения нелинейного элемента, работающего на данном участке, продлим его до пересечения в точке а с осью абсцисс и будем считать, что в точке пересечения напряжение U равно некоторой ЭДС Е. Для рис. 1.26, а справедливо следующее очевидное соотношение:
Ob = Oa + ab = Oa + bx tgβ.
Выразив в (1.44) отрезки через соответствующие электротехнические величины и масштабы напряжения и тока, получим
Ux /mu = E/mu + Ix /mi tgβ.
После умножения на масштаб напряжения будем иметь
| Ux = E + Ix | тu | = Е + Ix rd, |
| mi |
Полученному уравнению (1.45) согласно второму закону Кирхгофа соответствует схема замещения amb (рис. 1.26,б) нелинейного элемента, работающего на линейном участке cd.
Допустим, что нелинейный элемент получает питание от эквивалентного генератора с параметрами Eэ и r0э (рис. 1.26,б), заменяющего некоторый активный двухполюсник. Тогда по второму закону Кирхгофа можно написать
Eэ - E = Ix (r0э + rd ),
| Ix = | Eэ - E |
| r0э + rd |
Используя (1.45) и (1.46), нетрудно решать многие задачи, связанные с расчетом и анализом нелинейной электрической цепи. Например, по (1.46) можно определить ток Ix , а по (1.45) - напряжение Ux при заданных Eэ, r0э и rd .
Если графическое определение ЭДС E вызывает затруднение, можно найти ее, воспользовавшись выражением (1.45) и подставив в него известные координаты одной из точек участка cd.
