Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
2.9. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ r, L И С
Уравнение напряжений для цепи рис. 2.11, а имеет вид
Ū = Ūr + ŪL + ŪC.
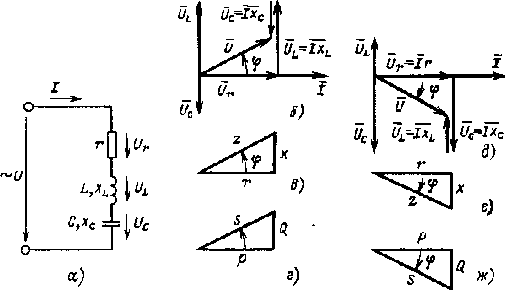 |
Рис. 2,11, Электри- ческая цепь, содер- жащая последова- тельно включен- ные r, L и С (а), ее векторная диаграм- ма (б), треуголь- ники сопротивле- ний и мощностей (в и г) цепи при xL > xC, векторная диаграмма (д), тре- угольники сопро- тивлений и мощ- ностей(e и ж) цепи при xC > xL |
Векторные диаграммы для цепи рис. 2.11, а изображены на рис. 2,11, б и в. Вектор напряжения на активном сопротивлении Ūr совпадает с вектором тока, вектор напряжения на индуктивности ŪL опережает вектор тока на 90°, вектор напряжения на емкости ŪС отстает от вектора тока на 90°. Следовательно, между векторами напряжения на индуктивности и емкости образуется угол 180°.
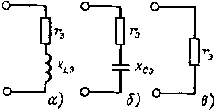 |
| Рис. 2.12. Эквивалентные схемы цепи, изображенной на рис. 2.11, а: а - хL > хС; б - хС > xL; в - хL = хС |
Если xL > хС, то и UL > UС и векторная диаграмма будет иметь вид, изображенный на рис. 2.11, б, а треугольник сопротивлений — на рис. 2.11, в, где x = xL - xС. Если хС > хL, то UC > UL и векторная диаграмма будет иметь вид, изображенный на рис. 2.11, д, а треугольник сопротивлений — на рис. 2.11, е, где х = хС - xL. Значение напряжения, приложенного к цепи,
U = √(Ur)2 + (UL - UC)2.
Выразив в (2.23) напряжение через ток и сопротивления, получим
U = √(Ir)2 + (IxL - IxC)2 = I√r2 + (xL - xC)2.
Последнее выражение представляет собой закон Ома для последовательной цепи r, L, С:
| I = | U | = | U | . |
| √r2 + (xL - xC)2 | z |
На основании проведенного анализа цепи, состоящей из последовательно соединенных r, L, С, можно сделать следующие выводы.
Если xL > xС, то напряжение сети опережает по фазе ток на угол φ:
u = Um sin (ωt + φ).
Цепь имеет активно-индуктивный характер.
Цепь может быть заменена эквивалентной цепью, изображенной на рис. 2.12, а. В эквивалентной схеме rэ = r, хэ = xL - xС = xLэ.
Если xС > xL, то напряжение сети отстает по фазе от тока на yгол φ:
и = Um sin (ωt - φ).
Цепь имеет активно-емкостный характер.
Цепь может быть заменена эквивалентной цепью, изображенной на рис. 2.12, б. В эквивалентной цепи rэ = r, xэ = хC - хL = xCэ.
