ЭЛЕКТРОТЕХНИКА

Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

2.12.  РЕЗОНАНС НАПРЯЖЕНИЙ

Известно, что в механической системе резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания механической системы, например колебания маятника, сопровождаются периодическим переходом кинетической энергии в потенциальную и наоборот. При резонансе механической системы малые возмущающие силы могут вызывать большие колебания системы, например большую амплитуду колебаний маятника.

В цепях переменного тока, где есть индуктивность и емкость, могут возникнуть явления резонанса, которые аналогичны явлению резонанса в механической системе. Однако полная аналогия - равенство собственной частоты колебаний электрического контура частоте возмущающей силы (частоте напряжения сети) — возможна не во всех случаях.

В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи представляет собой активное сопротивление. Такое состояние цепи имеет место при определенном соотношении ее параметров r, L, С, когда резонансная частота цепи равна частоте приложенного к ней напряжения.

Резонанс вэлектрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот.

При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках. В цепи, где r, L, С соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r, L, С соединены параллельно,— резонанс токов.

Рассмотрим явление резонанса напряжений на примере цепи рис. 2.11, а.

Как отмечалось, при резонансе ток и напряжение совпадают по фазе, т. е. угол φ = 0. и полное сопротивление цепи равно ее активному сопротивлению.

Это равенство, очевидно, будет иметь место, если xL = хС , т. е. реактивное сопротивление цепи равно нулю:

Выразив xL и xС соответственно через L, С и f, получим

2πfL =	1	,
	2πfC

откуда

f =	1	= fрез
	2π√LC

где f — частота напряжения, подведенного к контуру; fрез — резонансная частота.

Таким образом, при xL = xС в цепи возникает резонанс напряжений, так как резонансная частота равна частоте напряжения, подведенного к цепи.

Из   выражения   закона   Ома  для   последовательной   цепи

I =	U	.
	√r2 + (xL - xС)2

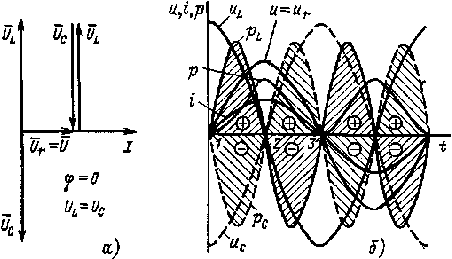Рис. 2.14. Векторная диаграмма (а) и графики мгновенных значений и, i, р (б) цепи рис. 2.11, а при резонансе напряжений

вытекает, что ток в цепи при резонансе равен напряжению, деленному на активное сопротивление:

Ток в цепи может оказаться значительно больше тока, который был бы при отсутствии резонанса. При резонансе напряжение на индуктивности равно напряжению на емкости:

При больших значениях xL и хC относительно r эти напряжения могут во много раз превышать напряжение сети. Резонанс в цепи при последовательном соединении потребителей носит название резонанса напряжений.

Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи:

На рис. 2.14, а изображена векторная диаграмма цепи рис. 2.11, а при резонансе напряжений Диаграмма подтверждает тот факт, что ток совпадает по фазе с напряжением сети и что напряжение на активном сопротивлении равно напряжению сети. Реактивная мощность при резонансе равна нулю:

так как UL = UC.

Полная мощность равна активной мощности;

так как реактивная мощность равна нулю. Коэффициент мощности равен единице:

Поскольку резонанс напряжений возникает, когда индуктивное сопротивление последовательной цепи равно емкостному, а их значения определяются соответственно индуктивностью, емкостью цепи и частотой сети,

xL = 2πfL,   xС =	1	.
	2πfС

Резонанс может быть получен или путем подбора параметров цепи при заданной частоте сети, или путем подбора частоты сети при заданных параметрах цепи.

На рис. 2.14, б изображены графики мгновенных значений тока i, напряжения и сети и напряжений иL , иC , иr на отдельных участках, а также активной р = iur и реактивной pL= iиL ,
pС = iиС мощностей за период для цепи рис. 2.11. а при резонансе напряжений. С помощью этих графиков можно проследить энергетическне процессы, происходящие в цепи при резонансе напряжений.

Активная мощность р все время положительна, она поступает из сети к активному сопротивлению и выделяется в нем в виде тепла. Мощности pL и рС знакопеременные, и, как видно из графика, их средние значения равны нулю.

В момент времени t = 0 (точка I на рис. 2.14, б) ток в цепи i = 0 и энергия магнитного поля
WL = 0. Напряжение на емкости равно амплитудному значению UтС, конденсатор заряжен и энергия его электрического поля

WC =	U2тcС	.
	2

В первую четверть периода, в интервале времени между точками 1 и 2, напряжение на емкости и, следовательно, энергия электрического поля убывают. Ток в цепи и энергия магнитного поля возрастают.

В конце первой четверти периода (точка 2) иС = 0, WС = 0. i = Im,  WL = I2mL/2.

Таким образом, в первую четверть периода энергия электрического поля переходит в энергию магнитного поля.

Так как площади pС(t) и pL(t) , выражающие запас энергии соответственно в электрическом и магнитном  полях, одинаковы, вся энергия электрического поля конденсатора переходит в энергию магнитного поля индуктивности. Во вторую четверть периода, в интервале между точками 2 и 3, энергия магнитного поля переходит в энергию электрического поля.

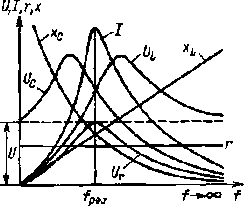Рис. 2.15. Графики зависимости I, r, хC, хL, Ur, UL , UC от частоты цепи, изображенной на рис  2.11, а

Аналогичные процессы происходят и в последующие четверти периода.

Таким образом, при резонансе реактивная энергия циркулирует внутри контура от индуктивности к емкости и обратно. Обмена реактивной энергией между источниками и цепью не происходит. Ток в проводниках, соединяющих источник с цепью, обусловлен только активной мощностью.

Для анализа цепей иногда используют частотный метод, позволяющий выяснить зависимость параметров цепи и других величин oт частоты.

На рис 2.15 изображены графики зависимости Ur, UC , UL , I, хC , хL , от частоты при неизменном напряжении сети.

При f = 0 сопротивления xL = 2πfL = 0,
хC = 1/2πfC = ∞, ток I = 0, напряжения Ur = Ir = 0,
UL = IxL= 0, UC = U.
При f = fpез хL = хC , I = U/r, UL = UC, Ur = U. При f→ ∞ xL→∞, хC→ 0, Ur → 0, UC → 0, UL → U.

В интервале частот от f = 0 до f = fpез нагрузка имеет активно-емкостный характер, ток опережает по фазе напряжение сети. В интервале частот f = fpез до f→ ∞ нагрузка носит активно-индуктивный характер, ток отстает по фазе от напряжения сети.

Наибольшее значение напряжения на емкости получается при частоте, несколько меньшей резонансной, на индуктивности - при частоте, несколько большей резонансной.

Явления резонанса широко используются в радиоэлектронных устройствах и в заводских промышленных установках.

Пример 2.4. Определить частоту сети, при которой в цепи рис. 2.11, а возникает резонанс напряжений. Определить также, во сколько раз напряжение на индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры:

Решение. Резонансная частота

fpез =	1	=	1	= 224 Гц.
	2π√LC		2•3,14•√0,1•5•10-6

Индуктивное сопротивление цепи при резонансе

Напряжение на индуктивности при резонансе

UL	=	IxL	,    UL = U	xL	= U	140	= 7U.
U		Ir		r		20

Напряжение на индуктивности при резонансе в 7 раз больше напряжения сети.