Глава шестая
ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
А. МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ
6.2. ОСНОВНЫЕ ВЕЛИЧИНЫ, ИСПОЛЬЗУЕМЫЕ ПРИ РАСЧЕТЕ И АНАЛИЗЕ МАГНИТНЫХ ЦЕПЕЙ. ЗАДАЧИ РАСЧЕТА И АНАЛИЗА
Магнитное поле в любой его точке характеризуется по интенсивности и направленности действия вектором магнитной индукции В. За направление магнитной индукции принимается направление, указываемое северным полюсом магнитной стрелки, помешенной в данную точку поля.
Магнитное поле может быть изображено с помощью линий магнитной индукции, касательные к которым во всех точках поля совпадают по направлению с векторами магнитных индукций.
Магнитное поле считается однородным, если векторы магнитных индукций во всех точках имеют одни и те же значение и направление. В противном случае поле считается неоднородным. Для определения направления магнитного поля проводника (рис. 6.2, а) и обмотки (рис. 6.2, б) пользуются правилом правоходового винта. Магнитное поле постоянного магнита (рис. 6.2, в) направлено вне магнита от северного полюса N к южному S. При некотором удалении от боковых краев полюсов поле в воздушном зазоре между полюсами магнита (а также электромагнита) можно считать однородным.
Величиной, служащей для интегральной оценки магнитною поля, является магнитный поток, представляющий собой поток вектора магнитной индукции сквозь поверхность. Магнитные потоки сквозь элемент поверхности dS (рис. 6.3) и поверхность S будут
| dФ = B dS = B cos α dS; Ф = | ∫ | B cos α dS. |
| s |
Когда магнитный поток проходит сквозь плоскость, расположенную перпендикулярно линиям магнитной индукции однородного поля, в (6.1) следует положить В = const и cos α = l. Тогда поток
Ф = ВS.
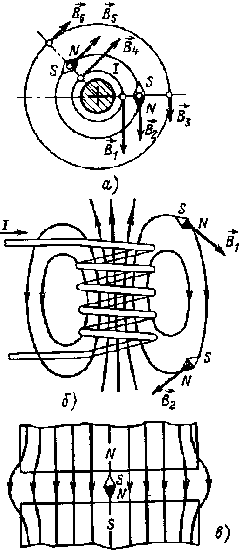 |
| Рис. 6.2. Картины магнитных полей прямолинейного проводника (а), катушки (б) и постоянного магнита (в) |
Единицами магнитного потока и магнитной индукции являются 1 вебер и 1 тесла (1 Вб = 1 В•с, 1 Тл = 1 Вб/м2 = 1 В•с/м2). Иногда для расчета используют устаревшие единицы магнитного потока и магнитной индукции 1 максвелл и 1 гаусс (1 Мкс = 10-8 Вб, 1 Гс = 10-4 Тл).
Степень участия среды в образовании магнитного поля характеризуется абсолютной магнитной проницаемостью среды, равной
μа = μ0μr ,
где μ0— магнитная постоянная; μr — относительная магнитная проницаемость.
В системе СИ единицей μ0 и μа является 1 генри/метр = 1 Гн/м, где 1 Гн = 1 Ом•с - единица индуктивности.
Магнитная постоянная μ0 = 4π • 10-7 Гн/м.
В электротехнике все вещества разделяют на ферромагнитные и неферромагнитные. К первым относятся сталь, никель, кобальт и их сплавы с различными присадками. Забегая несколько вперед, отметим, что у ферромагнитных материалов при определенных условиях μr >> 1 и μа >> μ0.
У неферромагнитных материалов, к которым относятся, например, медь, алюминий, дерево, пластмассы и воздух, μr ≈ 1 и μа ≈ μ0.
При расчете и анализе магнитных цепей пользуются обычно величиной Н, называемой напряженностью магнитного поля. Зная последнюю, можно определить магнитную индукцию
В = μаН.
Напряженность магнитного поля — величина векторная. В однородных по всем направлениям средах векторы В и Н по направлению совпадают.
Единицей напряженности магнитного поля является 1 А/м. Часто при расчетах используют более крупную единицу 1 А/см (1 А/см = 102 А/м).
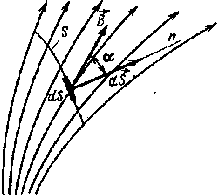 |
| Рис. 6.3. К определению магнитного потока |
Напряженность магнитного поля связана с токами, возбуждающими поле, законом полного тока, согласно которому линейный интеграл вектора напряженности магнитного поля вдоль замкнутого контура равен алгебраической сумме токов, охватываемых этим контуром:
∫○H dl = ∫○H cos α dl = ΣI.
Величину ΣI называют полным током или магнитодвижущей силой (МДС) и обозначают буквой F.
Со знаком «+» в (6.5) следует включать токи, положительные направления которых связаны правилом правоходового винта с произвольно выбранным направлением обхода контура интегрирования.
Если, например, контур интегрирования проходит внутри обмотки с числом витков w (рис. 6.4, а), то при обходе контура по часовой стрелке F= Iw. При обходе по часовой стрелке контура, проходящего внутри двух обмоток с различными направлениями токов (рис. 6.4, б), F= I1w1 - I2w2.
Рассмотрим в качестве примера магнитное поле в сечении замкнутого кольцевого магнитопровода из однородного материала (рис. 6.5). Линии магнитной индукции в кольце из любого материала при равномерном распределении витков представляют собой концентрические окружности. Выбрав за контур интегрирования линию магнитной индукции с радиусом ρ, получим
∫H cos α dl = Н • 2πρ = Iw,
откудаH = Iw/2πρ.
Если известна магнитная проницаемость μа материала кольца, то магнитная индукция будет
В = μаН = μаIw/2πρ.
Как видно, наибольшая магнитная индукция будет при ρ = ρ1, наименьшая — при ρ = ρ2. Если а << ρср = (ρ1 + ρ2)/2, то магнитные индукции при ρ1 и ρ2 будут отличаться незначительно. В этом случае магнитное поле можно считать практически однородным и определять магнитные индукцию и поток по формулам
| В = | μаIw | , Ф = BS = | μаIw | ab. |
| 2πρср | 2πρср |
На основании выражений (6.6) и (6,7) можно сделать следующие выводы.
Если F= Iw представляет собой МДС, то напряженность Н можно рассматривать как удельную МДС, приходящуюся на единицу длины контура интегрирования. При изготовлении колец (рис. 6.5) из материалов с различными значениями μа, напряженность Н будет одной и той же, а значения магнитной индукции В и, следовательно, магнитного потока Ф будут различными. Из сказанного следует, что напряженность Н является величиной, характеризующей систему проводников с токами, возбуждающую магнитное поле, а не само поле.
Предположим, что кольцо (рис. 6.5) выполнено из неферромагнитного материала, у которого μr1 ≈ 1 и μа1 ≈ μ0. Тогда для получений заданной магнитной индукции В согласно (6.7) потребуется МДС
I1w = В•2πρср/μа1= В•2πρср/μ0.
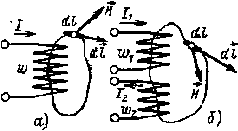 |
| Рис. 6.4. К пояснению закона полного тока |
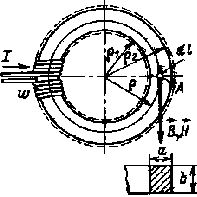 |
| Рис. 6.5. К расчету магнитного поля замкнутого кольца |
Если же изготовить кольцо из ферромагнитного материала, у которого μr2 >> 1 и μа2 = μr2μ0 >> μ0, получим те же значения магнитной индукции и, следовательно, магнитного потока при МДС
I2w = В•2πρср /μr2μ0.
Сравнивая выражения МДС в обоих случаях, нетрудно установить, что I2 = I1/μr2, т. е. I2 << I1. Приведенный пример подтверждает высказанное ранее положение о том, что изготовление магнитопровода из ферромагнитного материала приводит к существенному уменьшению тока, а значит, мощности, габаритных размеров и массы намагничивающих обмоток.
При расчете магнитных цепей приходится решать две задачи: наиболее часто встречающуюся прямую задачу и обратную задачу. Прямой считается задача, когда по известному магнитному потоку или магнитной индукции участка магнитопровода определяют МДС или ток намагничивающей обмотки. При решении обратной задачи, наоборот, МДС или ток считаются известными, а определению подлежат магнитный поток или магнитная индукция. При решении как прямой, так и обратной задач геометрические размеры и данные ферромагнитных материалов магнитопровода обычно считаются известными.
Кроме расчета нередко приходится решать задачи анализа магнитных цепей. Например, интересным и важным является вопрос о характере изменения магнитного потока при изменении МДС обмотки либо при изменении воздушного зазора в магнитопроводе, геометрических размеров магнитопровода и т. д.
