ЭЛЕКТРОТЕХНИКА

Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

2.4. ЦЕПЬ, СОДЕРЖАЩАЯ РЕЗИСТИВНЫЙ ЭЛЕМЕНТ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ r

В общем случае электрическая цепь переменного тока может содержать резистивные, индуктивные и емкостные элементы, параметрами которых соответственно являются сопротивление r, индуктивность L и емкость С. Анализ и расчет таких цепей значительно сложней, чем цепей постоянного тока. В цепях постоянного тока индуктивные и емкостные элементы проявляют себя только в моменты включения, отключения цепи или изменения ее параметров, когда изменяется ток и появляется ЭДС самоиндукции е = Ldi/dt в индуктивном

элементе и напряжение иС =	1	∫idt на емкостном элементе.
	С

В установившемся режиме ток в цепях постоянного тока не изменяется и ЭДС самоиндукции равна нулю, а напряжение на емкости иС соответствует   какому-то  постоянному значению.

В цепях переменного тока происходит непрерывное изменение напряжения и тока, в результате чего возникает изменяющаяся во времени ЭДС самоиндукции е и напряжение на емкости иС.

Таким образом, режим работы цепи переменного тока определяется не только сопротивлением r, но индуктивностью L и емкостью С. Прежде чем разбирать общий случай цепи с r, L и С, остановимся на частных случаях.

Рассмотрим цепь, содержащую только резистивный элемент с активным сопротивлением r. Под активным сопротивлением понимают сопротивление проводников переменному току. Вследствие вытеснения тока к поверхности проводника сопротивление проводника переменному току больше, чем постоянному. При малых частотах (несколько десятков и сотен герц) увеличение сопротивления незначительно и активное сопротивление определяется по той же формуле, что и сопротивление постоянному току. При частотах в сотни тысяч и миллионы герц активное сопротивление может оказаться намного больше сопротивления постоянному току и для его определения используют соответствующие формулы.

Мгновенное значение тока в цепи с активным сопротивлением (рис. 2.6, а) определяется по закону Ома:

Выразив u черезамплитудное значение

Рис 2.6. Электрическая цепь, содержащая резистивный элемент с активным сопротивлением r (а), ее векторная диаграмма (б) и графики мгновенных значений u, i, p (в)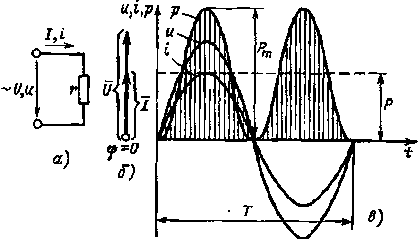

получим

где

Разделив левую и правую части на √2, получим закон Ома для цепи с активным сопротивлением, выраженный через действующие значения напряжения и тока.

Из выражения (2.3) следует, что ток и напряжение совпадают по фазе. Векторная диаграмма цепи изображена на рис. 2.6, б, а график мгновенных значений тока и напряжения — на рис. 2.6, в.

Мгновенная мощность цепи равна произведению мгновенных значений напряжения и тока:

Из графика мгновенной мощности (рис. 2.6, в) видно, что мощность изменяется от нуля до Рm , оставаясь все время положительной. Это означает, что в цепи с активным сопротивлением энергия все время поступает из сети к приемнику r и необратимо преобразуется в нем в теплоту, которая нагревает сопротивление и рассеивается в окружающей среде.

Среднее значение мощности за период

	1 T	T		1 Т	T		UmIm Т	T	1 - cos 2ωt dt = UmIm . 2 2
Pср =		∫	pdt =		∫	UmIm sin2 ωt dt =		∫
		0			0			0

Выразив амплитудные значения напряжения и тока через действующие значения, получим

После подстановки  U = Ir будем иметь

Из выражения (2.4) вытекает, что среднее значение мощности есть электрическая мощность, которая преобразуется в активном сопротивлении в теплоту. Такую мощность называют активной и обозначают символом Р.

К приемникам активной мощности относятся также электрические двигатели, в которых электрическая мощность преобразуется в механическую мощность, развиваемую двигателем на валу.

Активная мощность измеряется ваттметром, включенным соответствующим образом в электрическую цепь переменного тока.