Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.3. ПОДКЛЮЧЕНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ С РЕЗИСТИВНЫМ И ИНДУКТИВНЫМ ЭЛЕМЕНТАМИ К СЕТИ С ПОСТОЯННЫМ НАПРЯЖЕНИЕМ
После включения выключателя (рис. 4.3, а) в цепи возникает переходный процесс. Поскольку в цепи действуют три тока, необходимо составить три уравнения по законам Кирхгофа:
i = i1 + i2;
е = ir + i2r2 - U:
е = i2r2 - i1r1.
Совместное решение уравнений относительно тока i2 дает
| e ( | r1 + r | ) - i2 ( | r2r1 + r2r + rr1 | ) = - | U | . |
| rr1 | rr1 | r |
Выразив е через — L di2/dt, получим дифференциальное уравнение
| L | r1 + r | di2 | + ( | r2r1 + r2r + rr1 | ) i2 = | U | . | |
| rr1 | dt | rr1 | r |
Решением дифференциального уравнения без правой части (для свободного тока) будет выражение
i2св = Aept.
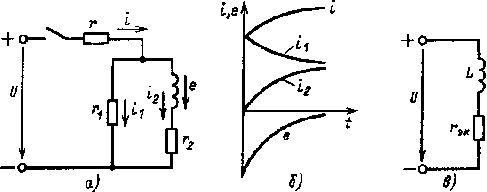 |
Рис. 4.3. Зависимости i(t), i1(t), i2(t), e(t) (б) при включении разветвленной цепи r, L (а) в сеть постоянного тока, эквивалентная относительно постоянной времени Т цепь (в) |
Значение р определяют из характеристического уравнения
| L | r1 + r | p + | r2r1 + r2r + rr1 | = 0 | . |
| rr1 | rr1 |
| p = - | r2r1 + r2r + rr1 | = - | 1 | . |
| (r1 + r)L | T |
| где T = | L(r1 + r) | — постоянная времени цепи. |
| r2r1 + r2r + rr1 |
Как видно, постоянная времени цепи определяется параметрами всех ее элементов, а не только ветви с индуктивностью.
Ток i2 в переходный период будет равен
i2 = i2уст + Аe-t/T.
Принужденный ток определяют из выражения (4.21а), в котором при t = ∞ di2 /dt = 0 и
| i2уст = I2уст = | Ur1 | . |
| r2r1 + r2r + rr1 |
Таким образом,
i2 = I2уст + Аe-t/T.
Значение А определяют с помощью первого закона коммутации: при t = 0 i2(0+) = i2(0-) = 0 и
А = - I2уст.
Ток i2 в переходный период будет равен
i2 = I2уст - I2уст e-t/T.
Подставив в (4.21) значение тока i2 и его производную, получим выражение для тока i1:
i1 = I1уст - (I1уст - I1нач)e-t/T,
| I1уст = | Ur2 | ; I1нач = | U | . |
| r2r1 + r2r + rr1 | r + r1 |
После подстановки i2 и i1 в (4.19) найдем выражение для тока i:
i = Iуст - (Iуст - Iнач)e-t/T,
| Iуст = | U(r1 + r2) | ; Iнач = | U | . |
| r2r1 + r2r + rr1 | r + r1 |
Выражение ЭДС е можно получить из (4.21) после подстановки в него вместо i2 и i1 их значений из (4.23) и (4.22):
| е = - еначe-t/T = - | U | r1e-t/T. |
| r + r1 |
На рис. 4.3, б изображены графики токов i(t), i1(t), i2(t) и ЭДС e(t) при включении цепи рис. 4.3, а (при r1 = r2).
Следует обратить внимание на то, что расчет токов вветвях разветвленных цепей с одним накопителем, например катушкой с индуктивностью L, можно значительно упростить и выполнить без составления и решения уравнений (4.19)— (4.21). Это можно сделать, если предварительно определить постоянную времени T цепи с помощью эквивалентной схемы (рис. 4.3, в). Для этого все резистивные элементы заменить одним эквивалентным относительно индуктивного элемента. Цепь, эквивалентная рис. 4.3, а, изображена на рис 4.3, в. Цепь эквивалентна только в отношении постоянной времени Т.
Эквивалентное сопротивление цени составит
| rэк = r2 + | rr1 | = | r2r + r2r1+ rr1 | . |
| r + r1 | r + r1 |
Постоянная времени эквивалентной цепи
| T = | L | = | L(r + r1) | . |
| rэк | r2r + r2r1 + rr1 |
Зная постоянную времени и определив начальные и установившиеся значения токов в ветвях, легко написать их выражения для переходного процесса в цепи. Они будут такими же, как и ранее полученные из решения системы уравнений.
Пример 4.1. Определить начальные в установившиеся значения токов i, i1, i2, ЭДС е, постоянную времени и длительность переходного процесса при включении цепи рис. 4.3, а в сеть постоянного тока. Параметры цепи: r = 2000 Ом, r1 = r2 = 3000 Ом, U= 200 В, L= 0,1 Гн.
Решение. Начальные значения токов:
| I2нач = 0; Iнач - I1нач = | U | = | 200 | = 0,04 А. |
| r + r1 | 2000 + 3000 |
Начальное значение ЭДС
Eнач = I1нач r1 = 0,04•3000 = 120 В.
Установившиеся значения токов и ЭДС:
| Iуст = | U | = | 200 | = | 200 | = 0,057 А; | ||
| r + | r1r2 | 2000 + | 3000•3000 | 3500 | ||||
| r1 + r2 | 3000 + 3000 | |||||||
| I1уст = | U - Iуст r | = | 200-0,057•2000 | ≈ 0,0285 A; |
| r1 | 3000 |
| I2уст = | U - I1уст r | = | 200-0,057•2000 | ≈ 0,0285 A; |
| r2 | 3000 |
Eуст = 0.
Постоянная времени контура
| T = | L(r1 + r) | = | 0,1(3000 + 2000) | = 2,38•10-5 с. |
| r2r1 + r2r + rr1 | 3000•3000 + 3000•2000 + 3000•2000 |
Длительность переходного процесса
t = 4Т = 9,6•10-5 с.
