Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
2.22. ЦЕПИ, СВЯЗАННЫЕ ВЗАИМНОЙ ИНДУКЦИЕЙ
Когда две катушки 1, 2 (рис. 2.29, а) расположены достаточно близко, так что часть Ф12 магнитного потока Ф1 (Ф1 = Ф'1 + Ф12), создаваемого током первой катушки, пронизывает вторую, а часть Ф21 магнитного потока Ф2 (Ф2 = Ф'2 + Ф21), создаваемого током второй катушки, пронизывает первую, между катушками возникает магнитная связь 1. На схемах магнитная связь обозначается фигурной скобкой и буквой М (рис. 2.29, б).
1 Картина магнитных полей значительно сложнее, чем та, что условно изображена на рис. 2.29, а для пояснения явления взаимной индукции. Предполагается, что Ф12 и Ф21 — эквивалентные магнитные потоки, сцепленные соответственно со всеми витками w2, w1.
Магнитная связь между катушками проявляется в том, что при изменении тока в катушках изменяются магнитные потоки и в катушках кроме ЭДС самоиндукции е1 = - w1 dФ1/dt,
e2= - w2 dФ2/dt возникают ЭДС взаимной индукции: во второй катушке - от потока Ф12
е12 = - w2 dФ12/dt, в первой - от потока Ф21 е21 = -w2 dФ21/dt.
Явление наведения ЭДС во втором контуре при изменении тока в первом называется явлением взаимной индукции.
Рассмотрим контур, состоящий из двух соединенных последовательно катушек, согласно (потоки Ф1, Ф2 действуют в одном направлении) и встречно (потоки Ф1, Ф2 действуют встречно).
Для обозначения согласного или встречного включения начала обмоток обозначаются жирными точками (рис. 2.29, б). Предполагается, что направления намотки катушек одинаковы (рис. 2.29, а).
Результирующая ЭДС возникающая в контуре при изменении тока в нем:
при согласном включении (рис. 2.29, б)
еэк = е1 + е2 + е12 + е21;
еэк = е1 + е2 - е12 - е21.
ЭДС самоиндукции и взаимной индукции могут быть выражены соответственно через индуктивность L ивзаимную индуктивность М. Если индуктивность L устанавливает количественное соотношение тока в катушке и создаваемого им потокосцепления L = Ψ/I, то взаимная индуктивность М устанавливает количественное соотношение между током первой катушки и создаваемым им потокосцеплением со второй катушкой М12 = Ψ12/I1 и соответственно М21 = Ψ21/I2.
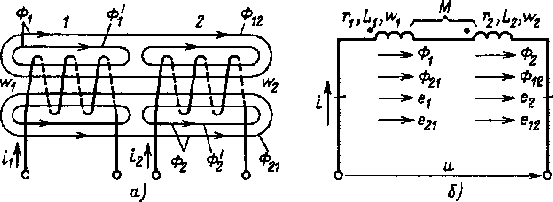 |
Рис. 2.29. К пояснению явления взаимной индукции (а), эквивалент- ная схема (б) |
сцепления L = Ψ/I, то взаимная индуктивность М устанавливает количественное соотношение между током первой катушки и создаваемым им потокосцеплением со второй катушкой М12 = Ψ12/I1 и соответственно М21 = Ψ21/I2.
Выразив в (2.29) и (2.30) соответствующие ЭДС через L и М иимея в виду, что M12 = M21 = M, получим 1:
1 Так как магнитные потоки Ф12, Ф21 расположены в одном и том же пространстве, магнитные сопротивления RM потокам будут одинаковыми и тогда Ф12 = I1w1/RM, Ф21 = I2w2/RM. Подставив Ф12 и Ф21 в выражения М12и М21, получим М12 = M21 = w1w2/RM = М.
при согласном включении
| Lэк | di | = L1 | di | + L2 | di | + 2M | di | ; |
| dt | dt | dt | dt |
при встречном включении
| Lэк | di | = L1 | di | + L2 | di | - 2M | di | ; |
| dt | dt | dt | dt |
Сократив (2.31), (2.32) на di/dt, получим эквивалентные значения индуктивности контура Lэк: при согласном включении
Lэк = L1 + L2 + 2M = L1 + L2 + 2k√L1L2;
Lэк = L1 + L2 - 2M = L1 + L2 - 2k√L1L2;
| k = | M | = | √ | Ф12Ф21 |
| √L1L2 | Ф1Ф2 |
- коэффициент магнитной связи между контурами. Так как Ф12 < Ф1,Ф21 < Ф2, то k < 1.
Умножив правые и левые части выражений (2.33), (2.34) на ω, получим:
хэк = х1 + х2 + 2хM;
хэк = х1 + х2 - 2хM;
Эквивалентное активное сопротивление в обоих случаях
rэк = r1+ r2.
Таким образом, электрическая цепь, состоящая из двух последовательно включенных, связанных взаимной индукцией катушек (рис. 2.30, а), может быть заменена эквивалентной цепью, изображенной на рис. 2.30, б.
Определение токов в параллельно включенных катушках с r и L, связанных взаимной индукцией (рис. 2.30, в), производится с помощью совместного решения двух уравнений, составленных по второму закону Кирхгофа,
I2(r2 + jx2)+ I1jxM = U.
Общий ток
I = I1 + I2.
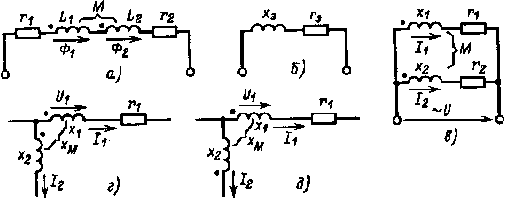 |
| Рис. 2.30. Последовательное (а) и параллельное (в) включения катушек, связанных взаимной индукцией, эквивалентная схема (б) последовательной цепи а; узлы сложных цепей с взаимно связанными индуктивностями (г и д) |
В сложных электрических цепях, когда две катушки, связанные взаимной индукцией, включены в разные ветви цепи (рис. 2.30, г, д),напряжение U1 имеет две составляющие, обусловленные собственной и взаимной индуктивностями: для схемы рис. 2.30, г
U1 = I1jx1 + I2jxM;
U1 = I1jx1 - I2jxM;
Знак плюс перед I2jxM означает, что направление тока I2 такое же, что и тока I1: от начала к концу катушки. Во втором случае ток I2 имеет направление от конца к началу катушки, а ток I1 — от начала к концу катушки, поэтому перед I2jxM стоит знак минус.
