Глава первая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
1.14. РАЗВЕТВЛЕННЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С НЕСКОЛЬКИМИ ИСТОЧНИКАМИ
Для расчета и анализа цепей с несколькими источниками используются различные методы, некоторые из которых будут рассмотрены далее. В том случае, когда в разветвленной электрической цепи с несколькими источниками имеется группа активных или пассивных элементов, соединенных последовательно или параллельно, следует для упрощения расчета и анализа заменить их соответственно одним эквивалентным пассивным пли одним активным элементом. Иногда может показаться целесообразным использовать преобразование треугольника резистивных элементов в звезду.
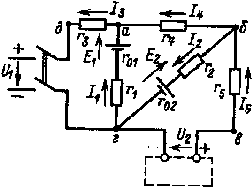 |
| Рис, 1.13. К расчету разветвленных электрических цепей с помощью законов Кирхгофа |
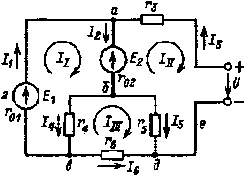 |
| Рис. 1.14 К пояснению метода контурных токов |
1.14,1. Метод законов Кирхгофа. Используя первый и второй законы Кирхгофа, можно для любой разветвленной электрической цепи составить необходимое число независимых уравнений и путем их совместного решения найти все подлежащие определению величины, например токи. Решая совместно уравнения, можно установить также зависимость между какими-либо величинами: между током и ЭДС, между двумя токами и т. д.
Перед составлением уравнений необходимо показать на схеме положительные направления известных и неизвестных величин. Сначала следует составить более простые уравнения по первому закону Кирхгофа, максимальное число которых должно быть на единицу меньше числа узловых точек. Недостающие уравнения следует составить по второму закону Кирхгофа.
В качестве примера составим схему уравнений для определения токов в электрической цепи, схема которой изображена на рис. 1.13. Будем считать, что ЭДС и напряжения с их направлениями, а также сопротивления известны. Поскольку данная цепь имеет пять ветвей с неизвестными токами, необходимо составить пять уравнений. Выбрав положительные направления токов I1, I2, I3, I4 и I5, для узлов а и б, а также для контуров агда, абга и бвгб при обходе последних по часовой стрелке получим.
- Е1 = - I1 (r1 + r01)- I3r3 - U1;
Е1 - Е2 = I1 (r1 + r01) + I2 (r2 + r02) - I4r4; Е2 == - I2 (r2 + r02) - I5r5 + U2.
1.14.2. Метод контурных токов. Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом законов Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно.
Дадим обоснование указанного метода.
Любая разветвленная электрическая цепь состоит из нескольких смежных контуров. Например, в электрической цепи ряс, 1.14 таких контуров три: абвга, бдвб и аедба. Каждый контур имеет несмежные ветви, принадлежащие лишь данному контуру, и смежные ветви, принадлежащие также соседним контурам. Так, контур абвга имеет несмежную ветвь вга и две смежные ветви аб и бв.
Допустим, что в каждом контуре рис. 1.14 имеется некоторый контурный ток, одинаковый для всех элементов контура. На ряс. 1,14 контурные токи обозначены II, III и IIII. Положительные направления контурных токов могут быть выбраны произвольно. Наложим на контурные токи следующее условие: контурные токи должны быть равны по абсолютному значению токам несмежных ветвей соответствующих контуров.
Если удастся найти контурные токи, то через них легко определять и токи всех ветвей. В силу наложенного условия токи несмежных ветвей следует определять так: если выбрать положительное направление тока несмежной ветвисовпадающим с контурным током, то ток ветви должен быть равен контурному току; если же направить ток несмежной ветви против контурного тока, то он должен быть равен контурному току со знаком «-». Так, токи в несмежных ветвях цепи (рис. 1.14) будут равны
Чтобы выяснить, как определять токи смежных ветвей, выразим ток I2 через токи I1 и I3 и заменим последние контурными токами: I2 = I1 + I3 = II — III. Аналогично найдем
Как видно, со знаком « + » должен быть взят тот контурный ток, направление которого совпадает с направлением тока смежной ветви; контурный ток, направленный в противоположную сторону, должен быть взят со знаком «-».
Нетрудно доказать, что контурные токи могут быть определены путем совместного решения системы уравнений, составленных по второму закону Кирхгофа, в которые вместо падений напряжения от токов ветвей следует ввести падения напряжения от контурных токов с соответствующими знаками.
Уравнение по второму закону Кирхгофа при включении внего контурных токов в общем случае имеет вид
ΣE = ΣIk r + ΣUk .
Для рассматриваемой цепи (рис. 1.14) уравнения будут:
Е1 - Е2 - I1(r01 + r02 + r4) - III r02 - IIIIr4;
0 = IIII (r4 + r5+ r6)- IIr4 - IIIr5.
При решении задач рассмотренным методом целесообразно выбирать положительные направления токов ветвей после определения контурных токов. В этом случае можно выбрать положительные направления токов ветвей так, чтобы все они совпадали с их действительными направлениями.
1.14.3. Метод узлового напряжения. Метод узлового напряжения дает возможность весьма просто произвести анализ и расчет электрической цепи, содержащей несколько параллельно соединенных активных и пассивных ветвей, например цепи, схема которой изображена на рис 1.15,а.
Пренебрегая сопротивлением проводов, соединяющих ветви цепи, схему рис. 1.15, а можно заменить более удобной для рассмотрения (рис. 1.15,б).
В зависимости от значений и направлений ЭДС и напряжений, а также значений сопротивлений ветвей между узловыми точками а и b установится определенное узловое напряжение Uab . Предположим, что оно направлено так, как показано на рис. 1.15, и известно. Зная напряжение Uab , легко найти все токи.
Выберем положительные направления токов, например так, как показано на рисунке. Тогда по второму закону Кирхгофа для контура, проходящего по первой ветви,
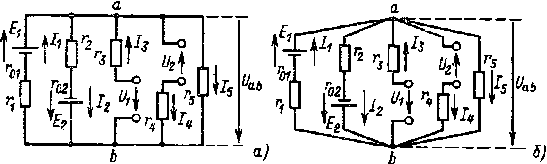 |
Рис. 1.15. К пояснению метода узлового напряжения |
откуда
| I1 = | Е1 - Uab | = (Е1 - Uab)g1. |
| r1 + r01 |
Поступая аналогичным способом, нетрудно получить формулы для токов I2, I3 и I4:
I2 = (Е2 + Uab)g2, I3 = (U1 - Uab )g3, I4 = (U2 + Uab)g4.
По закону Ома для пятой ветви
I5 = Uab /r5 = Uab g5.
Для вывода формулы, позволяющей определить напряжение Uab , напишем уравнение по первому закону Кирхгофа для узла а:
После замены токов их выражениями (1.37) - (1.39) и преобразований получим
| Uab = | Е1g1 - Е2g2 + U1g3 - U1g4 | , |
| g1 + g2 + g3 + g4 + g5 |
Формула узлового напряжения в общем случае имеет вид
| Uab = | ΣЕg + ΣUg | . |
| Σg |
Перед определением напряжения по формуле (1.40) следует задаться его положительным направлением. Со знаком « + » в(1.40) должны входить ЭДС, направленные между точками а и b встречно напряжению Uab и напряжения ветвей, направленные согласно с Uab. Знаки в формуле (1.40) не зависят от направления токов ветвей.
При анализе и расчете электрических цепей методом узлового напряжения целесообразно выбирать положительные направления токов после определения узлового напряжения. В этом случае положительные направления токов нетрудно выбрать таким образом, чтобы все они совпадали с их действительными направлениями.
Пример 1.3. В электрической цепи рис. 1.15, б Е1 = 40 В, Е2 = 20 В, r01 = r02 = 1 Ом, r1 = 9 Ом, r2 = 39 Ом, r3 = 10 Ом, r4 = 30 Ом, r5 = 15 Ом, U1 = 45 В, U2 = 30 В.
Пользуясь методом узлового напряжения, определить токи в ветвях.
Решение. По формулам (1.37) — (1.40) при указанных положительных направлениях напряжения Uab и токов
| Uab = | Е1/(r1 + r01) - Е2/(r2 + r02) + U1/r3 - U2/r4 | = 21,54 B; |
| l/(r1 + r01) + l/(r2 + r02) + 1/r3 + l/r4 + 1/r5 |
I2 = (E2 + Uab )/(r2 + r02 ) = 1,04 A;
I3 = (U1 - Uab)/r3 = 2,35 A;
I4 = (U2 + Uab )/r4 = 1,72 A;
I5 = Uab /r5 = 1,44 A
1.14.4. Метод наложения. Метод наложения основан на том, что в линейных электрических цепях ток любой ветви может быть определен как алгебраическая сумма токов от каждого источника в отдельности.
Расчет электрических цепей методом наложения производят в таком порядке. Из электрической цепи удаляют все источники ЭДС и напряжения, кроме одного. Сохранив в электрической цепи все резистивные элементы, в том числе и внутренние сопротивления источников, производят расчет электрической цепи. Внутренние сопротивления источников с указанными напряжениями полагают равными нулю. Подобным образом поступают столько раз, сколько имеется в цепи источников.
Результирующий ток каждой ветви определяют как алгебраическую сумму токов от всех источников. Для того чтобы результирующие токи совпадали с действительными направлениями, целесообразно выбирать положительные направления результирующих токов после определения токов от всех источников.
Метод наложения весьма удобен для анализа явлений, происходящих в электрических цепях при изменении их параметров.
Например, используя метод наложения, нетрудно определить характер изменения токов ветвей в цепи (см. рис. 1.15) при увеличении
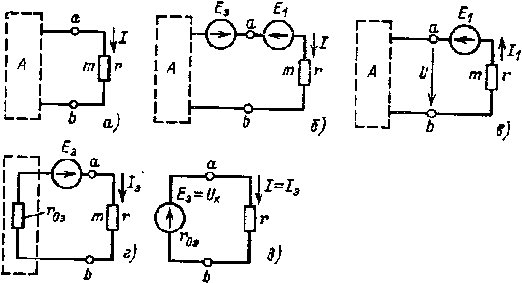 |
Рис. 1.16. К пояснению метола эквивалентного генератора |
ЭДС Е1 до Е'1. Действительно, предположим, что при некоторых параметрах цепи до увеличения Е1 установились токи, действительные направления которых совпадают с указанными на рисунке. Для решения задачи заменим мысленно увеличение ЭДС Е1 введением в первую ветвь дополнительного источника с r0доп = 0 и Едоп = Е'1— Е1. После этого удалим из цепи все источники, кроме источника с ЭДС Едоп, и определим действительные направления дополнительных токов от этого источника, которые очевидны.
Поскольку дополнительный ток первой ветви Iдоп будет совпадать по направлению с током I1, для определения результирующего тока первой ветви следует воспользоваться формулой
I'1 = I1 + I1доп. На основании данной формулы можно сделать вывод о том, что при увеличении Е1 ток I1 будет возрастать. К такому же выводу можно прийти и в отношении токов других ветвей, кроме третьей.
Так как дополнительный ток третьей ветви I3доп направлен против тока I3, то для определения результирующего тока нужно использовать формулу I'3 = I3 — I3доп. В отношении результирующего тока третьей ветви можно сделать такой вывод: при увеличении ЭДС Е1 ток I3 будет сначала уменьшаться, при некотором значении Е1 окажется равным нулю, а при дальнейшем увеличении Е1 изменит направление (I3 < 0) и по абсолютному значению будет возрастать.
1.14.5. Метод эквивалентного генератора. Метод эквивалентного генератора дает возможность упростить анализ и расчет электрических цепей в том случае, когда требуется определить ток, напряжение или мощность лишь одной ветви.
Предположим, что требуется найти ток I ветви amb некоторой электрической цепи (рис. 1.16, а), остальные элементы которой сосредоточены в пределах прямоугольника, представляющего собой активный двухполюсник А.
Согласно методу наложения ток I не изменится, если в данную ветвь ввести два источника, ЭДС которых Е1 и Еэ равны и направлены в разные стороны (рис. 1.16,б). Ток I можно определить тогда как разность двух токов I = Iэ - I1, где I1 — ток, вызванный всеми источниками двухполюсника А и ЭДС Е1 (рис, 1.16, в): Iэ — ток, вызванный только ЭДС Еэ (рис. 1.16, г).
Если выбрать ЭДС Е1 таким образом, чтобы получить I1 = 0, то ток I будет равен
| I = Iэ = | Еэ |
| r0э + r |
Так как при I1 = 0 (рис. 1.16,в) активный двухполюсник А будет работать относительно ветви amb в режиме холостого хода, то между выводами а и b установится напряжение холостого хода U = Ux и по второму закону Кирхгофа получим E1 = I1r + Ux = Ux . Но по условию Еэ = Е1. поэтому и Еэ = Ux . Учитывая это, формулу для определения тока I можно записать в такой форме:
| I = | Еэ | = | Ux | . |
| r0э + r | r0э + r |
В соответствии с (1.41) электрическая цепь рис. 1.16,а может быть заменена эквивалентной цепью рис. 1.16, д, в которой Еэ = Ux и r0э следует рассматривать как ЭДС и внутреннее сопротивление некоторого эквивалентного генератора. В результате возможности такой замены и возникло название изложенного метода
Значения Еэ = Ux и r0э можно определить как расчетным, так и экспериментальным путем. Для расчетного определения Ux и r0э необходимо знать параметры элементов активного двухполюсника А и схему их соединения. При определении сопротивления r0э необходимо удалить из схемы двухполюсника все источники, сохранив все резистивные элементы, в том числе и внутренние сопротивления источников ЭДС. Внутренние сопротивления источников с указанными напряжениями следует принять равными нулю.
Пример 1.4. В электрической цепи рис. 1.17, а U = 100 В, Е = 40 В, r1 = r4 = 30 Ом, r2 = r3 = 20 Ом, r = 15 Ом, r0 = 1 Ом. Пользуясь методом эквивалентного генератора, определить ток I и напряжение Uab .
Решение. При отключенном резистивном элементе r (рис. 1.17,б) по закону Ома и на основании второго закона Кирхгофа
| I1 = | U | = 2 А, I2 = | U | = 2 А, |
| r1 + r3 | r2 + r4 |
Еэ = Ux = Е - I1r1 + I2r2 = 20 В.
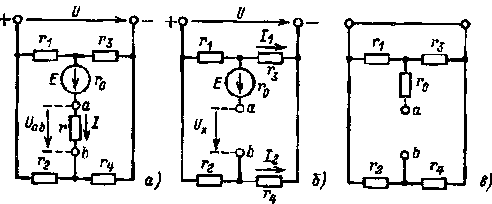 |
Рис. 1.17. Схемы электрических цепей к примеру 1,4 |
После мысленного удаления из схемы рис. 1.17, б источников получим схему, изображенную на рис. 1,17,в. Глядя на эту схему, можно сделать заключение о том, что между точками а и b последовательно соединены три участка: участок с параллельно соединенными резисторами r1 и r3; участок, на котором параллельно соединены резисторы r2 и r4; участок, содержащий только резистор r0. В соответствии сэтим внутреннее сопротивление эквивалентного генератора (сопротивление цепи относительно точек а и b) будет
| r0э = | r1r3 | + | r2r4 | + r0 = 25 Ом. |
| r1 + r3 | r2 + r4 |
По формуле (1.41) и закону Ома
| I = | Ux | = 0.5 A, Uab = Ir = 7,5 В. |
| r + r0э |
