ЭЛЕКТРОТЕХНИКА

Глава третья
ТРЕХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

3.3. СООТНОШЕНИЯ МЕЖДУ ФАЗНЫМИ И ЛИНЕЙНЫМИ НАПРЯЖЕНИЯМИ ИСТОЧНИКОВ. НОМИНАЛЬНЫЕ НАПРЯЖЕНИЯ

Фазные напряжения источника отличаются от его ЭДС вследствие падений напряжения во внутренних сопротивлениях источника, а напряжения приемника отличаются от напряжений источника за счет падений напряжения в сопротивлениях проводов электрической сети. Вопрос об учете влияния падений напряжения в проводах сети на напряжения приемников будет рассмотрен в § 3.8. Пока же для упрощения анализа соотношений в трехфазных цепях будем пренебрегать указанными падениями напряжения.

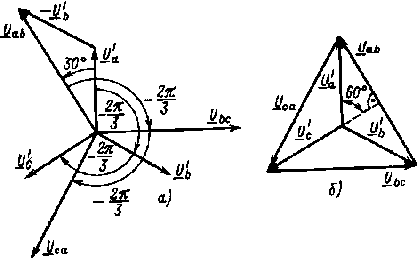Рис. 3.5. Векторные диаграммы фазных и линейных напряжений при соединении источника звездой

Применяя второй закон Кирхгофа поочередно ко всем фазам, при сделанном допущении и соединении источников звездой (см. рис. 3.3) получим

На основании выражений (3.3) можно сделать вывод о том, что если генератор имеет симметричную систему ЭДС, то его фазные напряжения тоже симметричны, а векторная диаграмма фазных напряжений (рис. 3.5, а) не отличается от векторной диаграммы ЭДС генератора (рис. 3.2, б).

На основании уравнений по второму закону Кирхгофа для контуров N1abN1, N1bсN1и N1caN1 (см. рис. 3.3) нетрудно получить следующие уравнения, связывающие линейные и фазные напряжения:

Используя (3.4) и имея векторы фазных напряжений (рис. 3.5, a), можно построить векторы линейных напряжений Uab , Ubc и Uca .

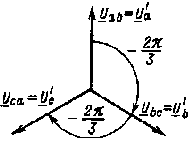Рис. 3.6. Векторная диаграмма фазных и линейных напряжений при соединении источника треугольником

Из векторной диаграммы рис. 3.5, а следует, что при соединении источника звездой линейные напряжения равны и сдвинуты по фазе относительно друг друга на угол 2π/3. Векторы линейных напряжений изображают чаще соединяющими векторы соответствующих фазных направлений, как показано на рис. 3.5, б.  Из  векторной диаграммы  рис.  3.5, б следует,  что

Такое же соотношение существует между любыми другими линейными и фазными напряжениями. Поэтому можно написать, что вообще при соединении источника звездой

Выражения (3.3) справедливы и при соединении источника треугольником (см. рис. 3.4). Непосредственно из схемы рис. 3.4 следует, что линейные напряжения равны соответствующим фазным напряжениям:

Можно написать, что при соединении источника треугольником вообще

Векторная диаграмма фазных и линейных напряжений при соединении источника треугольником приведена на рис.  3.6.

На основании изложенного можно сделать следующие выводы.

Независимо от способа соединения фаз источника между линейными проводами трехфазной цепи существуют три одинаковых по действующему значению линейных напряжения, сдвинутых по фазе относительно друг друга на угол 2π/3. В случае соединения фаз источника звездой линейные напряжения оказываются в √3 раз больше, чем при соединении фаз того же источника треугольником.

В четырехпроводной цепи кроме трех линейных напряжений между линейными проводами и нейтральным проводом имеются три фазных напряжения. Последние в √3 раз меньше линейных напряжений и сдвинуты по фазе относительно друг друга также на угол 2π/3. Фазные и линейные напряжения не совпадают по фазе.

Наиболее распространенными номинальными напряжениями приемников переменного тока являются напряжения 380, 220 и 127 В. Напряжения 380 и 220 В используют преимущественно для питания промышленных приемников, а напряжения 220 и 127 В - для бытовых приемников. Напряжения 380, 220 и 127 В считают также номинальными напряжениями трехфазных электрических сетей. При линейном напряжении 380 В фазное напряжение четырехпроводной трехфазной сети 380/√3 = 220 В, а при линейном напряжении 220 В оно составляет 220/√3 = 127 В. Наличие в четырехпроводных сетях линейных и фазных напряжений дает возможность подключать однофазные приемники, рассчитанные на два напряжения, например на 380 и 220 В или 220 и 127 В.