ЭЛЕКТРОТЕХНИКА

Глава шестая
ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
Б. МАГНИТНЫЕ  ЦЕПИ С ПЕРЕМЕННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ

6.13. ЭКВИВАЛЕНТНЫЙ ТОК И ВЕКТОРНАЯ ДИАГРАММА ИДЕАЛИЗИРОВАННОЙ ОБМОТКИ

С целью упрощения расчета и анализа магнитных цепей переменного тока несинусоидальный ток обмотки заменяют эквивалентным в отношении действующего значения синусоидальным током. Такая замена позволяет использовать для расчета и анализа методы, изложенные в гл. 2 (в частности, комплексный метод), а также производить построение векторных диаграмм.

Для определения действующего значения I эквивалентного синусоидального тока можно было бы воспользоваться выражением, приведенным в гл. 2,

I =	√	1	T   ∫ i2(t)dt, 0
		T

для него необходимо предварительно построить график i(t) несинусоидального тока согласно методике, изложенной в § 6.11. Однако указанный способ определения тока I практически непригоден, так как, не говоря уже о его сложности, для этого потребовалось бы иметь набор динамических петель гистерезиса для разных частот и максимальных значений магнитной индукции.

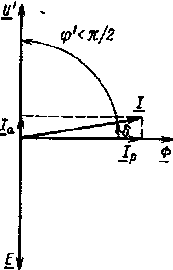Рис- 6.28. Векторная диа­грамма идеализированной обмотки

Практические способы определения действующего значения I эквивалентного синусоидального тока будут рассмотрены далее, а пока будем считать, что он уже известен, и рассмотрим векторную диаграмму идеализированной обмотки (см. рис. 6.21, б). Последнюю (рис. 6.28) нетрудно построить, используя выражения (6.22), (6.23) и (6.26), а также тот факт, что идеализированная обмотка потребляет кроме реактивной (индуктивной) мощности также и активную мощность. Учитывая это, можно утверждать, что эквивалентный синусоидальный ток будет отставать  по фазе относительно напряжения  u' на  некоторый угол φ', который можно определить из формулы

P' = ΔРc = U'I cos φ'.

Ток I можно разложить на две составляющие: активную составляющую Iа, обусловленную потерями мощности ΔРc в ферромагнитном магнитопроводе, и реактивную (индуктивную) составляющую Iр, необходимую для возбуждения основного магнитного потока; последней соответствует реактивная (индуктивная) мощность Q'.

Очевидно

В магнитных цепях, особенно при наличии воздушного зазора, ток Iр и мощность Q' обычно намного превышают ток Iа и мощность Р' = ΔРc. В соответствии с этим угол δ, называемый углом потерь, составляет обычно несколько градусов, а угол φ' близок к 90°.

Активная и реактивная мощности идеализированной обмотки могут быть выражены следующим образом:

Реактивная мощность необходима для возбуждения магнитного потока как в ферромагнитной, части магнитопровода, так и в воздушном зазоре. Поэтому она может быть выражена так:

где Qc = U'Iр.с и Iр.с — мощность и ток, необходимые для возбуждения магнитного поля в ферромагнитной части магнитопровода; Qδ = U'Iδ и Iδ — мощность и ток, необходимые для создания магнитного потока в воздушном зазоре.

Ток I идеализированной обмотки определяют часто через его составляющие Iа и Iр, которые для ферромагнитной части магнитопровода  находят  через  соответствующие  мощности:

Реактивная составляющая тока Iδ определяется по формуле

Мощности  P' = ΔРc  и Qc находят следующим образом:

где р и Qуд — удельные потери мощности и удельная реактивная мощность, т. е. мощности, приходящиеся на единицу массы магнитопровода, Вт/кг и вар/кг; m — масса магнитопровода, кг.

Для определения удельных потерь мощности пользуются иногда следующей формулой, полученной на основании обобщения опытных данных:

где п = 5,69 lg	p1,5	; p1,5 и p1,0 — удельные потери мощности при частоте 50 Гц и максимальных
	p1,0

значениях магнитной индукции 1,5 и 1,0 Тл, Вт/кг. Показатель степени n в формуле (6.34) для многих ферромагнитных материалов близок к двум. Формула (6.34) пригодна для расчетов при изменении Вm от 0,5 до 1,6 Тл и f от 10 до 100 Гц.

Так как магнитная индукция Вm пропорциональна напряжению U', а п ≈ 2, можно сделать вывод о том, что при увеличении напряжения U' потери мощности в магнитопроводе существенно возрастают. Из формулы (6.34) следует также, что потери мощности в значительной степени зависят от частоты переменного тока.

Если отсутствуют сведения об удельной реактивной мощности, то реактивный ток Iр,с может быть определен приближенно с помощью выражения действующего значения тока, приведенного в гл. 2, и графика iр,с(t) (рис. 6.29), построение которого производится в той же последовательности, что и графика i(t) (см. рис. 6.25). Для построения графика iр,с(t) необходимо использовать магнитную характеристику Ф (iр,с), расчет которой следует производить с помощью закона полного тока, используя основную кривую намагничивания.

Как следует из графика iр,с(t) (рис. 6.29), при Ф = 0 (что соответствует u' = ± U'm) ток iр,с = 0. Это является подтверждением того, что эквивалентный синусоидальный ток будет в данном случае действительно чисто реактивным. Задача расчета значительно упрощается, если при амплитудном значении напряжения u' ферромагнитный материал магнитопровода не насыщен или незначительно насыщен (участок 1—2 рис. 6.29). В этом случае ток iр,с можно считать синусоидальным и график iр,с(t) не строить. Из расчета магнитной цепи достаточно найти амплитуду тока Iр,с m , после чего легко определить его действующее значение по формуле 

Iр,с= Iр,с m/√2.

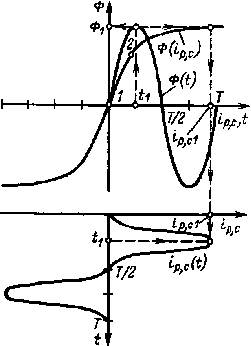Рис. 6.29. К построению графика реактивной составляющей тока

В некоторых случаях для определения эквивалентного синусоидального тока катушки пользуются кривой намагничивания ферромагнитного материала при переменном токе Вm(Н~), представляющей собой зависимость амплитуды магнитной индукции от действующего значения напряженности магнитного поля, соответствующей действующему значению тока катушки. График Вm(Н~) аналогичен основной кривой намагничивания и отличается от последней только количественными соотношениями между напряженностью и магнитной индукцией.

Учитывая, что Н~ и I соответствуют эквивалентным синусоидальным напряженности и току, по закону полного тока для однородного ферромагнитного участка магнитной цепи (рис. 6.21, б) можно написать

откуда нетрудно найти ток I. Реактивную составляющую тока можно определить по формуле (6.28), если предварительно найти активную составляющую.

Если магнитопровод содержит несколько ферромагнитных участков и воздушных зазоров с различными площадями поперечного сечения, то активную и реактивную составляющие тока I следует определять по формулам

где х — номер участка из ферромагнитного  материала,  х = 1, 2, ..., k; у — номер воздушного зазора, у = 1, 2,  ..., n;

токи Iax и Iр,сx определяются согласно методике, изложенной выше при рассмотрении магнитной цепи (см. рис. 6.21, б), ток Iδy — по формуле (6.32).

В заключение следует обратить внимание на то, что с увеличением воздушного зазора в магнитопроводе при U' = const ток Iδ и мощность Qδ значительно возрастают, тогда как токи Ia и Iр,с, а также мощности Р' = ΔРc и Qc остаются без изменения.