Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
2.17. ИЗОБРАЖЕНИЕ НАПРЯЖЕНИЙ И ТОКОВ КОМПЛЕКСНЫМИ ЧИСЛАМИ И ВЕКТОРАМИ НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
Запишем комплексное число в виде
Im = Imеjα = Im cos α + jIm sin α
Допустим, что вектор комплексного числа Im вращается с постоянной угловой частотой ω и угол α = ωt + ψ. Тогда
Im = Imеj(ωt + ψ) = Im cos (ωt + ψ) + jIm sin (ωt + ψ).
Слагаемое Im cos (ωt + ψ) представляет собой действительную часть комплексного числа и обозначается
Im cos (ωt + ψ) = ReImеj(ωt + ψ).
Слагаемое Im sin (ωt + ψ) есть коэффициент при мнимой части комплексного числа и обозначается
Im sin (ωt + ψ) = ImImеj(ωt + ψ).
Легко видеть, что коэффициент при мнимой части комплексного числа представляет собой выражение мгновенного значения синусоидального тока
i = Im sin (ωt + ψ)
и является проекцией вращающегося вектора Im на мнимую ось комплексной плоскости.
Синусоидально изменяющиеся по времени величины изображаются на комплексной плоскости для момента времени t = 0. Тогда комплексная амплитуда Im записывается в виде
Im = Imejψ,
Таким образом, комплексная амплитуда изображает синусоидальный ток на комплексной плоскости для момента времени t = 0.
Допустим, что в электрической цепи мгновенные значения напряжений и тока имеют выражения
i = Im sin (ωt + ψ2).
Комплексные амплитуды напряжения и тока должны быть записаны в виде
Im = Imejψ2;
Обычно принято выражать в виде комплексных чисел не амплитуды, а действующие значения напряжений и токов:
| U = | Um | ejψ1 - Uejψ1, I = | Im | ejψ2 = Iejψ2. |
| √2 | √2 |
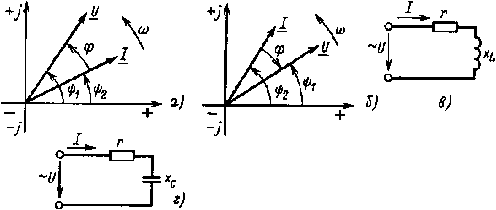 |
Рис. 2.24. Изображение напряжения и тока в виде векторов на комплексной плоскости (а и б) электрических цепей (в и г) |
Если ψ1 > ψ2, то векторы напряжения и тока расположены на комплексной плоскости так, как показано на рис. 2.24, а. Напряжение опережает по фазе ток, так как векторы вращаются против часовой стрелки и, следовательно, цепь имеет активно-индуктивный характер (рис. 2.24, в).
При ψ2 > ψ1 (рис. 2.24, б) ток опережает по фазе напряжение и цепь имеет активно-емкостный характер (рис 2.24, г).
