Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.1.ОБЩИЕ ВОПРОСЫ И ОПРЕДЕЛЕНИЯ
Процессы, протекающие в электромагнитах, механических и тепловых системах при переходе из одного установившегося (стационарного) состояния к другому, при котором энергия системы (соответственно энергия электрического и магнитного полей, кинетическая энергия и тепловая энергия и обусловливающие их величины — напряжение, ток, скорость и температура) изменяется, называются переходными или неустановившимися процессами.
Процесс перехода от одного установившегося состояния к другому протекает не мгновенно (скачком), а постепенно в течение определенного времени в силу того, что энергия скачком изменяться не может и, следовательно, не может изменяться скачком обусловливающая ее величина. Если предположить, что энергия изменится мгновенно за время t = 0, то мощность, необходимая для этого,
| P = | dw | = | w | = ∞ |
| dt | 0 |
В электрических цепях, содержащих в общем случае резистивный, индуктивный и емкостный элементы, переходный процесс возникает при включении, выключении и изменении параметров цепи. Такие действия в общем случае называют коммутацией электрической цепи или просто коммутацией. После коммутации изменяется энергия индуктивного WL = I2L/2 и емкостного
WС = CU2/2 элементов. Поскольку энергия мгновенно изменяться не может, следовательно, не может изменяться мгновенно ток в индуктивности и напряжение на емкости. Из этого вытекают два важных положения (их называют законами коммутации), без знания которых невозможно рассчитывать и анализировать переходные процессы в электрических цепях.
Первый закон коммутации: ток в ветви с индуктивностью после коммутации iL(0+) (включение, отключение, изменение параметров цепи) при t = 0+ имеет то же значение, что и до коммутации iL(0-):
iL(0+) = iL(0-).
Второй закон коммутации: напряжение на емкости после коммутации uC(0+) при t = 0+ имеет такое же значение, что и до коммутации:
uC(0+) = uC(0-).
Аналогичные законы есть и в механике, например скорость тела (массы) после начала действия силы при t = 0+ равна скорости до начала действия силы.
При расчетах переходных процессов используют так называемые начальные значения тока и напряжения в ветвях цепи, которые в совокупности с законами коммутации позволяют определить постоянные интегрирования. Под начальными значениями тока и напряжения понимают их значения до коммутации при t = 0_. Необходимо отметить, что ток в ветви только с одним резистивным элементом изменяется скачком по той причине, что энергия в нем не накапливается, а все время преобразуется необратимо в теплоту и ее значение w = uit пропорционально времени, а мощность р = dw/dl = ui имеет конечное значение.
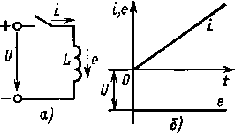 |
| Рис. 4.1. Зависимости i(t), e(t)(б) при подключении идеальной катушки с индуктивностью L (а) к сети с постоянным напряжением |
Общность переходных процессов в механических системах и электрических цепях можно проследить на примере протекания процесса при действии силы Fна тело с массой т и при включении индуктивного элемента с индуктивностью L к источнику с постоянным напряжением.
Известно, что сила, действующая на тело, связана с массой и ускорением законом Ньютона.
F = mdv/dt ,
dv/dt = F/m.
Скачкообразное изменение скорости тела, когда dv/dt= ∞, невозможно, так как сила может иметь конечное, а не бесконечно большое значение.
При включении идеальной катушки (r = 0) с индуктивностью L (рис. 4.1, a) под действием напряжения сети в ней возникает ток и ЭДС самоиндукции. Идеальные индуктивности существуют реально — это обмотки электромагнитных исследовательских устройств элементарных частиц, выполненные из сверхпроводящих материалов, сопротивление которых при криогенных температурах равно нулю.
Из выражения, составленного по второму закону Кирхгофа,
U = -e = L di/dt
di/dt = U/L,
| i = | U | t + A. |
| L |
Сопоставляя (4.1) и (4.3), можно заключить, что индуктивность по своему действию аналогична массе в механической системе.
Из выражения (4.4) следует, что при определенном конечном значении U скорость изменения тока в индуктивности имеет определенное конечное значение. На рис. 4.1, б изображены графики тока i и ЭДС е при включении цепи по рис. 4.1, а.
В системах автоматического управления часто происходит нарушение установившихся режимов и они практически работают в условиях переходного режима. В большинстве систем автоматического управления используются электротехнические устройства, поэтому необходимо рассмотреть переходные процессы хотя бы в простейших электрических цепях.
