ЭЛЕКТРОТЕХНИКА

Глава шестая
ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
А. МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ

6.8. ОСНОВЫ РАСЧЕТА НАМАГНИЧИВАЮЩИХ ОБМОТОК

Задача расчета намагничивающей обмотки состоит в том, чтобы при заданной МДС определить конструктивные параметры обмотки, а также потребляемые ею ток и мощность.

Различают два типа намагничивающих обмоток:

а) параллельные или шунтовые;

б) последовательные или  сориесные.

Параллельную обмотку рассчитывают на включение на одно из стандартных напряжений U сети постоянного тока (рис. 6.17). Она изготовляется из проволоки относительно небольшого диаметра, имеет сравнительно большие число витков и сопротивление. Ток параллельной обмотки определяется напряжением источника и сопротивлением обмотки:

I = U/rш.

Последовательную обмотку ОС (рис. 6.18) включают последовательно с каким-либо элементом ЭЛ электрической цепи (например, с обмоткой якоря или возбуждения двигателя), и, таким образом, в обмотке и данном элементе существует один и тот же ток. Последовательная обмотка изготовляется из проволоки относительно большого диаметра, имеет небольшое число витков и сопротивление rс , значение которого намного меньше сопротивления rэл . Ток обмотки определяется практически напряжением источника и сопротивлением элемента, последовательно с которым включена обмотка:

I = U/(rэл + rс) = U/rэл.

При расчете обмотки прежде всего следует определить площадь ее поперечного сечения Sк (рис. 6.19) и установить, разместится ли она в окне магнитопровода площадью S0 = ab.

Площадь Sк можно определить из соотношения

Sкk = Sw,

где k = Sw/Sк- коэффициент заполнения, показывающий, какая часть площади S, заполнена проводниковым материалом, обычно медью; S и w — площадь поперечного сечения проволоки и число витков катушки.

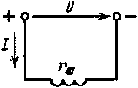Рис. 6.17. Схема включения параллельной намагничивающей обмотки

Рис. 6.18. Схема включения последовательной намагничивающей обмотки

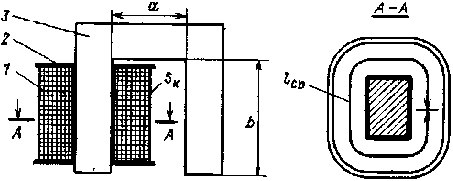Рис. 6.19. Эскиз намагничивающей обмотки

Коэффициент заполнения зависит от толщины изоляции проволоки и способа намотки. Так, если изготовить катушку из проволоки с тонкой эмалевой изоляцией и укладывать проволоку виток к витку, то коэффициент заполнения будет иметь наибольшее значение.

Выразив S через ток I и допустимую по условиям нагревания плотность тока J, получим

Как видно, площадь Sк, а значит, размеры и масса обмотки при выбранных значениях k и J, зависят исключительно от МДС F= Iw обмотки.

Определив по формуле (6.17) площадь Sк, можно изобразить эскиз обмотки (рис. 6.19) и найти длину среднего витка lср. После этого из выражения

r =	U	=	ρlсрw	.
	I		S

нетрудно определить площадь поперечного сечения и диаметр проволоки обмотки:

S =	ρlсрF	;  d =	√	4S	=	√	4ρlсрF	,
	иU			π			πU

а   затем   ток,   мощность,   число   витков   и   сопротивление   обмотки:

I = SJ =	ρlсрJF	;    P = UI = ρlсрJF;
	U

w =	F	=	U	;   r =	U	=	U2	.
	I		ρlсрJ		I		ρlсрJF

Как видно из полученных формул, при повышении напряжения обмотки ее число витков и сопротивление возрастают, а ток, площадь поперечного сечения и диаметр проволоки уменьшаются. Мощность обмотки не зависит от напряжения, а при увеличении МДС она возрастает.

Исходной величиной при расчете последовательной обмотки является ее ток. Зная МДС и ток, легко определить число витков: W = F/I, а далее найти и другие величины.

Пример 6.2, Установить, разместится ли обмотка, МДС которой была определена в примере 6.1, в окне магнитопровода (см. рис. 6.9, а), если допустимая плотность тока J = 2 А/мм2, а коэффициент заполнения k = 0,5.

Решение. По формуле (6.16) площадь, занимаемая обмоткой в окне магнитопровода.

Sк =	Iw	=	2754	= 2754 мм2.
	Jk		2•0,5

Площадь окна магнитопровода (см. рис. 6.9, a)

S0 = 110•95 = 10450 мм2.

Так как Sк < S0, то обмотка разместится в  окне магнитопровода.