ЭЛЕКТРОТЕХНИКА

Глава шестая
ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
А. МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ

6.5.  НЕРАЗВЕТВЛЕННЫЕ МАГНИТНЫЕ ЦЕПИ

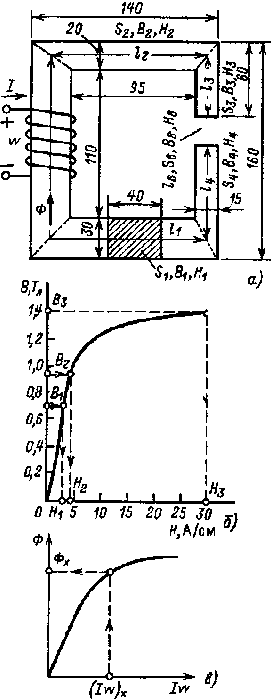Рис. 6.9.  К анализу и расчету неразветвленных магнитных цепей

6.5.1. Основные соотношения. Пусть имеется неразветвленная магнитная цепь (рис. 6.9, а) некоторого электротехнического устройства. Во всех участках неразветвленной цепи магнитный поток имеет одно и то же значение, поэтому

Ф = B1S1= B2S2 = ...= BδSδ,

откуда B1/B2 = S2/S1, B1/Bδ = Sδ/S1 и т. д.

Как видно, в неразветвленной цепи отношение магнитных индукций участков обратно отношению их площадей поперечного сечения.

Чтобы установить соотношения между напряженностями различных участков магнитных цепей, воспользуемся кривой намагничивания (рис. 6.9, б). Как видно, для создания магнитного потока на участках, материал которых насыщен, требуется значительно большая напряженность магнитного поля, чем на участках, материал которых не насыщен. Например, если В3 = 2В1, то Н3 > 2Н1.

Особенно большие напряженности требуются для создания магнитного потока в воздушных зазорах. Так, при Вδ = В3 Нδμ0 = H3μ0μr3, откуда

Нδ = H3μr3. Обычно μr3 >> 1, поэтому при

Вδ = В3 Нδ >> H3.

На основании (6.9) для магнитной цепи рис. 6.9, а можно написать

Так как Н = B/μа, а Ф = BS, то из (6.10) следует, что чем больше длины участков магнитной цепи, тем большая МДС требуется для получения заданного магнитного потока. К увеличению МДС приводит также уменьшение площадей поперечного сечения участков, так как при этом возрастают магнитные индукции и, следовательно, напряженности. Если увеличивать длины или уменьшать площади поперечного сечения при заданной МДС, то это приведет к уменьшению магнитного потока. Особенно большое влияние на значение МДС при Ф = const и на значение магнитного потока при Iw = const оказывают изменение длины или площади поперечного сечения воздушного зазора.

Для выявления влияния параметров магнитной цепи на магнитный поток и МДС удобно воспользоваться приводимым ниже выражением (6.11), которое называют иногда законом Ома для магнитной цепи. Это выражение нетрудно получить из (6.10), если заменить в нем каждый

член левой части выражением	Фl	= ФRм с соответствующими индексами:
	μаS

Ф =	Iw									=
	l1	+	l2	+	l3	+	lδ	+	l4
	μа1S1		μа2S2		μа3S3		μ0Sδ		μа4S4

где Rм = Rм1 + Rм2 + Rм3 + Rмδ + Rм4 — магнитное сопротивление неразветвленной магнитной цепи, равное сумме магнитных сопротивлений отдельных ее участков.

При анализе магнитной цепи с помощью выражения (6.11) следует помнить, что вследствие непостоянства величин μа1, μа2, μа3 и μа4 зависимость Ф(Iw) получается нелинейной, а также что сопротивление Rмδ обычно превышает сумму остальных сопротивлений.

6.5.2. Последовательность расчета. Чтобы ознакомиться с последовательностью решения прямой задачи, обратимся к следующему примеру.

Пример 6.1. Определить МДС и ток обмотки, если в воздушном зазоре магнитной цепи рис. 6.9, а требуется получить Вδ = 1,4 Тл. Число витков обмотки w = 1000, кривая намагничивания стали приведена на рис. 6.9, б.

Решение. Разбив магнитную цепь на участки, находим их длины и площади поперечного сечения: l1 = 252,2 мм, S1 = 1200 мм2, l2 = 117,5 мм, S2 = 800 мм2, l3 = 50 мм, S3 = Sδ = S4 = 600 мм2, l4 = 83 мм, lδ = 2 мм.

Дальнейшее решение условимся проводить в единицах СИ.

Магнитный поток и магнитные индукции Ф = BδSδ= 1,4•600•10-6 Вб; В1 = Ф/S1 = 0,7 Тл, аналогично В2 = 0,93 Тл; В3 = В4 = Вδ = 1,4 Тл.

По кривой намагничивания находим Н1 = 3 А/см = 300 А/м, Н2 = 400 А/м, Н3 = Н4 = 3000 А/м.

Напряженность магнитного поля в воздушном зазоре

Нδ = Вδ/μ0 =	1,4	=112•104  А/м.
	4π•10-7

МДС и ток обмотки

Iw = H1l1 + H2l2 + H3(l3 + l4) + Hδlδ = 300•252,5 + 400•117,5 + 3000•133 + 112•104•2•10-3 =

= 75,8 + 47 + 399 + 2240 = 2762 А,

или Iw = ΣHст lст + Hδlδ = 522 + 2240 = 2762 А, т. е. I = Iw/w = (ΣHст lст + Hδlδ)/w = Iст + Iδ = 0,522 + 2,24 = 2,762 A.

Как видно, несмотря на малый воздушный зазор наибольшие составляющие МДС и тока обмотки необходимы для создания магнитного потока именно в воздушном зазоре.

Чтобы ознакомиться с последовательностью решения обратной задачи, допустим, что в той же магнитной цепи (см. рис. 6.9, а) требуется найти магнитный поток Фx при заданной МДС (Iw)x .

Решить эту задачу путем однократного применения уравнения (6.10) не представляется возможным, так как оно содержит четыре неизвестные величины: H1, H2, H3 = H4 и Нδ . Нельзя решить задачу и с помощью формулы (6.11), поскольку в ней кроме магнитного потока Ф неизвестными являются также магнитные проницаемости μа1, μа2 и μа3 = μа4 .

Обратные задачи решают в таком порядке:

1. задаются несколькими значениями магнитного потока и, решая несколько раз прямую задачу, находят соответствующие этим потокам МДС обмотки;
2. строят магнитную характеристику, представляющую собой зависимость магнитного потока от МДС обмотки Ф(Iw) (рис. 6.9, в);
3. пользуясь магнитной характеристикой, находят магнитный поток Фх по заданной МДС (Iw)x .

Наибольший магнитный поток, которым следует задаваться, можно определить, считая, что
Н1 = Н2 = Н3 = Н4 = 0, а заданная МДС расходуется лишь для создания магнитного потока в воздушном зазоре.

6.5.3. Магнитные характеристики. Кроме указанной выше зависимости Ф(Iw) под магнитной характеристикой понимают также зависимость магнитного потока от тока обмотки

Ф (I).

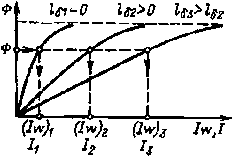Рис. 6.10. Магнитные характеристики при различных воздушных зазорах

Магнитные характеристики применяют не только для решения обратной задачи расчета магнитных цепей. Их широко используют также при анализе работы и расчете многих электромагнитных устройств, например генераторов, двигателей и др.

Соотношение между магнитным потоком и МДС или током и, следовательно, конфигурация магнитной характери­стики существенно зависят от параметров магнитопровода, особенно от длины  воздушного зазора.

Если магнитопровод имеет одинаковую площадь поперечного сечения по всей длине и не имеет воздушных зазоров, то магнитные характеристики Ф(Iw) и Ф(I) совпадают с основной кривой намагничивания В(Н), так как в этом случае Ф = BS, а

I= Hl/w.

Для получения того же магнитного потока при введении в магнитную цепь воздушного зазора требуются значительно большие значения МДС и тока, поскольку в данном случае I = (Hl+ Hδlδ)/w и обычно Нδ >> Н. В соответствии с этим магнитные характеристики Ф(Iw) при различных воздушных зазорах выглядят, как показано на рис. 6.10. В другом масштабе по оси абсцисс они представляют собой магнитные характеристики Ф(I), так как I = (Iw)/w.

Как видно, при увеличении воздушного зазора магнитные характеристики все более спрямляются.

6.5.4. Индуктивность и взаимная индуктивность. Как известно, индуктивность, через которую может быть определена ЭДС, индуктируемая в обмотке электромагнитного устройства, выражается следующим образом: L = dΨ/dI.

Если обмотка не имеет ферромагнитного магнитопровода, то между потокосцеплением Ψ и током I существует линейная зависимость, а поэтому L = dΨ/dI= Ψ/I = const.

Когда обмотка имеет ферромагнитный магнитопровод, то, не учитывая потоков рассеяния, можно считать, что один и тот же магнитный поток Ф сцеплен со всеми витками w катушки. Тогда Ψ = wФ и L = dΨ/dI = wdФ/dI.

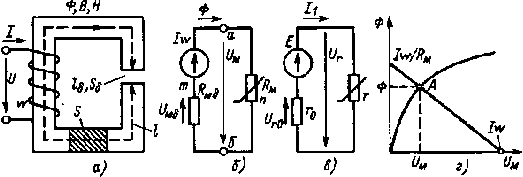Рис.   6. 11.   К   пояснению   аналогии   методов   расчета   магнитных   и электрических цепей

Чтобы рассмотреть особенности индуктивности обмотки с ферромагнитным магнитопроводом, обратимся к магнитным характеристикам Ф(I), приведенным  на рис. 6.10.

Пока ферромагнитный материал не насыщен, между магнитным потоком и током существует примерно линейная зависимость, а поэтому L= wdФ/dI ≈ wФ/I≈ const. Значение индуктивности в этом случае, особенно при lδ = 0, намного превышает значение индуктивности такой же обмотки без ферромагнитного магнитопровода.

По мере насыщения ферромагнитного материала индуктивность уменьшается, а когда наступает полное насыщение ферромагнитного материала, она становится равной индуктивности такой же обмотки без ферромагнитного магнитопровода.

При введении в магнитопровод воздушного зазора или при его увеличении индуктивность уменьшается и может быть принята примерно постоянной в большем диапазоне изменения тока.

Все сказанное об особенностях индуктивности обмотки с ферромагнитным магнитопроводом в полной мере относится и к взаимной индуктивности двух обмоток, расположенных на общем магнитопроводе.

6.5.5. Аналогия методов расчета магнитных и электрических цепей.

Так как при анализе и расчете магнитных цепей используются законы, подобные законам Ома и Кирхгофа для электрических цепей, то для большей наглядности иногда заменяют магнитные цепи их схемами замещения, подобными схемам замещения электрических цепей.

Рассмотрим возможность такой замены на примере простейшей магнитной цепи, изображенной на рис. 6.11, а.

На основании закона полного тока

Подобное по структуре уравнение можно написать и для некоторой электрической цепи (рис. 6. 11, в):

В уравнениях (6.12) и (6.13) величинамианалогами являются: МДС Iw и ЭДС Е; магнитный поток Ф и ток I1; магнитные напряжения Uм = Hl = ФRм, Uмδ = Hδlδ = ФδRм и электрические напряжения Ur = I1r, Ur0 = I1r0; магнитные сопротивления Rм , Rмδ и электрические сопротивления r, r0.

Следует заметить, что значение магнитного сопротивления зависит от напряженности магнитного поля, а поэтому является нелинейным. В соответствии с этим нелинейным должно быть и сопротивление r.

Схема электрической цепи, соответствующая уравнению (6.13), приведена на рис. 6.11, в, а схема замещения магнитной цепи, соответствующая уравнению (6.12), — на рис. 6.11, б.

Учитывая подобие схемы замещения магнитной цепи и схемы нелинейной электрической цепи, для решения обратной задачи расчета магнитной цепи можно воспользоваться методом, изложенным в § 1.16, основанным на графическом решении двух уравнений с двумя неизвестными. Для этого необходимо рассчитать и построить график зависимости Ф(Uм) для нелинейной части апб схемы замещения магнитной цепи; рассчитать и построить график зависимости Ф = f(Uм) для линейной части атб схемы замещения магнитной цепи.

Точка пересечения А указанных графиков (см. рис. 6.11, г) определит значения  магнитного  потока  Ф   и  магнитного  напряжения   Uм .

Зависимости Ф(Uм) и Ф = f(Uм) называются веберамперными характеристиками (вб. а. х.). Их построение производится с помощью уравнений, составленных по закону полного тока, для контуров, в которые должно входить интересующее нас магнитное напряжение Uм .

Так, для расчета вб. а. х. Ф(Uм), изображенной на рис. 6.11, г, необходимо составить уравнение для контура апба (рис. 6.11, б), которое будет иметь вид

0 = ФRм - Uм = Hl - Uм ,

откуда Uм = ФRм = Hl.

Расчет вб. а. х. производится в такой последовательности: задаются несколькими значениями магнитных потоков Ф, по формуле В = Ф/S определяют соответствующие значения В, после чего по кривой намагничивания В (Н) находят напряженности; далее по приведенному выше выражению подсчитывают магнитные напряжения Uм .Чтобы рассчитать вб. а. х. Ф = f(Uм), показанную на рис. 6.11, г, следует составить уравнение для контура атба:

Iw = ФRмδ + Uм = Hδlδ + Uм ,

откуда

Uм = Iw - ФRмδ = Iw - HδIδ

Так как Rмδ = lδ/μ0S0 = const, то график Ф = f(Uм) представляет собой прямую линию и может быть построен, например, по следующим двум точкам:

1) при Ф = 0 Uм = Iw;

2) при Uм = 0 Ф = Iw/Rмδ .

Когда магнитопровод имеет (кроме воздушного зазора) несколько участков с различными площадями поперечного сечения или материалами, их необходимо заменить предварительно одним участком, имеющим эквивалентную вб. в. х. Ф(Uм). Замену следует производить, исходя из того, что при последовательном соединении участков во всех участках существует один и тот же магнитный поток.