ЭЛЕКТРОТЕХНИКА

Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

2.21. РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ

При расчете сложных цепей с одним источником (рис. 2.25, а) целесообразно использовать метод преобразования сложной цепи в простейшую эквивалентную цепь.

Вначале записывают комплексные значения полных сопротивлений отдельных последовательных участков цепи:

Затем определяют комплексное значение полного эквивалентного сопротивления Zab участка цепи между точками ab:

Zab =	Z2Z3	= rab + jxab.
	Z2 + Z3

В результате цепь может быть преобразована в эквивалентную, изображенную на рис. 2.25, б, где сопротивления Z2, Zab и Z4 включены последовательно.

Комплексное значение  полного  сопротивления   всей   цепи

Таким образом, эквивалентная схема цепи будет иметь вид, изображенный на рис. 2,25, в.

Общий ток цепи

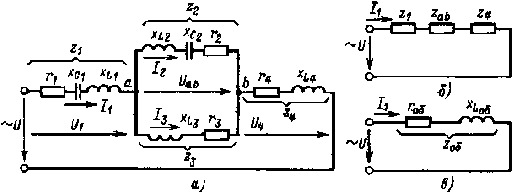Рис. 2.25. Сложная цепь (а)и ее эквивалентные схемы (б, в)

Напряжение Uab между точками ab

Токи I2 и I3 на основании закона Ома

Полная мощность цени

Для проверки правильности решения целесообразно построить векторную диаграмму, а также подсчитать активную и реактивную мощности всех участков цепи и сопоставить их с результатами, полученными при помощи формулы комплексного значения мощности.

Расчетные значения токов и напряжений изображают в виде векторов на комплексной плоскости. Затем строят векторную диаграмму напряжений по уравнению

и векторную диаграмму токов по уравнению

Если взаимное расположение векторов токов и напряжений на отдельных участках цепи соответствует характеру нагрузки и многоугольники напряжений и токов получаются замкнутыми, значит, решение правильное. Векторная диаграмма токов и напряжений цепи рис. 2.25, а с параметрами, заданными в примере 2.6, изображена на рис. 2.26.

Активная мощность всех участков цепи должна быть равна

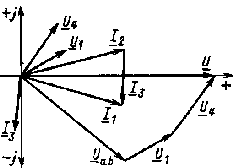Рис.   2.26.    Векторная   диаграмма цепи, изображенной на рис. 2.25, а

действительной части Р комплексного значения полной мощности:

а реактивная мощность — мнимой части Q комплексного значения полной мощности:

При выполнении этого условия решение следует считать правильным.

Пример 2.6. Определить токи I1, I2, I3, напряжения U1, Uab и U4 цепи, изображенной на рис. 2.25, а. Построить векторную диаграмму токов и напряжений, а также определить активные и реактивные мощности цепи.

Параметры цепи: r1 = 15 Ом, r2 = 30 Ом, r3 = 60 Ом, r4 = 10 Ом, xL1 = 35 Ом, xL2 = 20 Ом, xL3 = 80Ом, xL4 = 25 Ом, xC1 = 20 Ом, xC2 = 60 Ом.  Напряжение сети  U = 300 В.

Решение. Комплексные значения полных сопротивлений последовательных участков цепи

Комплексное значение полного сопротивления участка цепи между точками аb

Zab =	Z2Z3	= 46,4 - j20,6.
	Z2 + Z3

Комплексное значение полного сопротивления всей цепи

Вектор напряжения сети совмещают с  положительной  действительной осью комплексной плоскости:   U = Uеj0 = 300. Комплексное значение тока I1

Напряжения Uab , U1 и U4 равны

Токи I2 и I3 составляют

На рис. 2.26 отложены комплексные значения токов и напряжений. На том же рисунке изображена векторная диаграмма напряжений и токов. Векторная диаграмма напряжений строится на основании уравнения, составленного по второму закону Кирхгофа:

а векторная диаграмма токов - на основании уравнения, составленного по первому закону Кирхгофа: I1 = I2 + I3. Полная мощность цепи

Активная мощность всех участков цепи

равна действительной части комплексного значения полной мощности.

Реактивная мощность всех участков цепи

равна мнимой части комплекса полной мощности.

Следовательно, задача решена правильно.

Пример 2.7. Определить характер нагрузки и параметры эквивалентных цепей схем, изображенных на рис 2.27, а и б, если xL > хС.

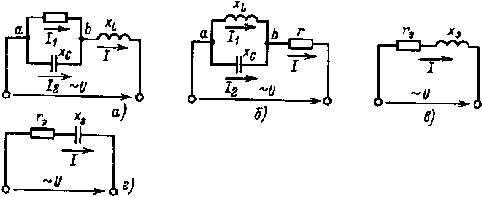Рис.   2.27.  Электрические  цепи  (а,  б) и  их эквивалентные схемы (в, г) к примеру 2.7

Рис. 2.28. Сложная цепь с несколькими источниками (а); действительные (положительные) направления ЭДС, напряжения и тока генератора (б), приемника (в)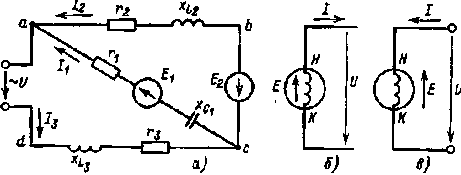

Решение. Характер нагрузки легко определить путем анализа реактивной мощности цепи

а) Для цепи рис. 2,27, а: так как I = √I12 + I22, то I2 < I и, следовательно,

Характер нагрузки цепи активно-индуктивный. Эквивалентная схема цепи изображена па рис. 2.27, в.

Параметры эквивалентной схемы: Zэк = Zab + jxL = rэк + jxэк .

б) Для цепи рис. 2.27, б: так как xL > хC , то I1 = Uab /xL < I2 = Uab /xC и
QC = I22xC = I2Uab > QL = I12xL = I1Uab.

Характер нагрузки цепи активно-емкостный. Эквивалентная схема цепи изображена на рис. 2.27,г.

Параметры   эквивалентной   цепи  схемы:   Zэк = Zab + r = rэк - jxэк.

Расчет сложных цепей с несколькими источниками производится   теми   же   методами,   что   и   цепей   постоянного   тока:

методом непосредственного использования первого и второго законов Кирхгофа;

методом контурных токов;

методом двух узлов;

методом эквивалентного генератора и т. п.

Рассмотрим  первый  метод на  примере   цепи   рис.   2.28, а.

Поскольку цепь имеет три ветви, неизвестными являются три тока. Для их определения необходимо составить три уравнения.

Прежде чем составлять уравнения, следует указать на схеме действительные (положительные) направления ЭДС и напряжений   источников   в   соответствии   со   схемой   их   включения.

За действительное (положительное) направление ЭДС и тока в обмотках генераторов принимают направление от конца к началу обмотки (рис. 2.28, б), напряжения, наоборот,— от начала к концу.

Если внутреннее сопротивление источника мало и им можно пренебречь (Z = 0), то

Затем необходимо указать произвольно предполагаемые направления токов в каждой из ветвей, выбрать произвольно направление обхода контура и составить необходимое число уравнений. Первое уравнение составляют по первому закону Кирхгофа:

второе и третье уравнения — по второму закону Кирхгофа. Одно из них составляют для контура acda (направление обхода контура по часовой стрелке): другое — для контура аbса:

Из совместного решения уравнений определяют комплексные значения токов I1, I2 и I3.

Проверить правильность решения задачи можно с помощью векторной диаграммы или баланса активных и реактивных мощностей. Для этого необходимо подсчитать активную и реактивную мощности, развиваемые источниками и потребляемые всеми элементами цепи. Для расчета активной и реактивной мощностей приемников, как указывалось, используют формулы P = I2r, QL = I2хL, QC = I2хC.

Труднее определять соответствующие мощности источников, так как в сложных цепях некоторые из источников могут работать в режиме приемника.

О режиме работы источника нельзя судить по взаимным направлениям тока, ЭДС или напряжения, как это было в цепях постоянного тока. В цепях постоянного тока в результате решения задачи определяются не только значения, но и действительные направления токов, что дает возможность по взаимным направлениям тока, ЭДС или напряжения источника судить о режиме его работы, поскольку мощность Р = UI, Р = ЕI.

В цепях переменного тока активная и реактивная мощности равны соответственно P = UI cos φ; P = ЕI cos φ; Q = UI sin φ; Q = EI sin φ, т. е. зависят не только от взаимных направлений токов, ЭДС и напряжений, но и косинуса и синуса соответственно, угла сдвига  φ по фазе между током и напряжением или током и ЭДС, который в сложных цепях может быть больше 90°.

Режимы работы источника по активной и реактивной мощностям могут быть установлены при соответствующих взаимных действительных (положительных) направлениях величин Е, I и U, I по знакам активной и реактивной мощностей, развиваемых источником, полученным в результате расчета электрической цепи.

Для источника, работающего в режиме генератора, действительные (положительные) направления Е, I и U, I соответствуют указанным на рис. 2.28, б, работающего в режиме потребителя - на рис. 2.28, в.

Если в результате расчета активная и реактивная мощности для рис, 2.28, б и в оказались положительными, то действительно в первом случае источник работает в режиме генератора (отдает активную и реактивную индуктивную мощность), во втором — в режиме потребителя (потребляет активную и реактивную индуктивную мощности. Если же значения мощностей оказались отрицательными, то в первом случае источник работает в режиме потребителя, а во втором — в режиме генератора.

В разветвленных цепях с несколькими источниками после нанесения произвольно положительных направлений токов в ветвях, что необходимо для составления расчетных уравнений по законам Кирхгофа, уже условно определены режимы работы источников. Например, для цепи рис. 2.28, а предполагается, что источник с ЭДС Е1 работает в режиме генератора, а источники с ЭДС Е2 и напряжением U — в режиме приемника. Если же направления токов изменить, то изменится и предполагаемый режим работы источников. Естественно, что от выбора направлений токов действительный режим работы источников не изменится.

Как уже говорилось, действительный режим работы источников будет установлен после расчета электрической цепи и определения мощности каждого из источников. Допустим, мощность источника с ЭДС Е1 цепи (рис. 2.28, а)оказалась положительной, источника с ЭДС Е2 — отрицательной, источника с напряжением U — положительной. Это означает, что источник с ЭДС Е1 работает врежиме генератора, как и условно предполагалось, источник с ЭДС Е2 работает в режиме генератора, а не в режиме приемника, как это предполагалось до получения результатов расчета, источник с напряжением U работает в режиме приемника, как и предполагалось.