ЭЛЕКТРОТЕХНИКА

Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

2.13. РАЗВЕТВЛЕННЫЕ ЦЕПИ

Параллельное соединение приемников. Вначале рассмотрим графоаналитический метод расчета цепи с параллельным соединением потребителей (рис. 2.16, а). Для такой цепи характерно то, что напряжения на каждой ветви одинаковы, общий ток равен сумме токов ветвей.

Ток в каждой ветви определяется по закону Ома:

I1 =	U	; I2 =	U	; I3 =	U	(xL3 > xC3).
	√r12 + xL12		√r22 + xC22		√r32 + (xL3 - xC3)2

Угол сдвига φ между током каждой ветви и напряжением определяют с помощью cos φ:

cos φ1 =	r1	;   cos φ2 =	r2	; cos φ3 =	r3	.
	√r12 + xL12		√r22 + xC22		√r32 + (xL3 - xC3)2

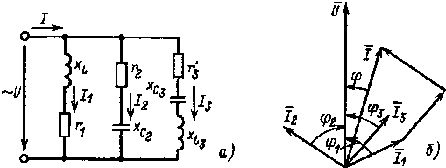Рис.   2.16.   Цепь   с  параллельным  соединением   потребителей   (а)   и ее векторная диаграмма (б)

Общий ток в цепи, как следует из первого закона Кирхгофа, равен геометрической сумме токов всех ветвей:

Значение общего тока определяют графически по векторной диаграмме рис. 2.16, б.

Активная мощность цепи равна арифметической сумме активных мощностей всех ветвей:

Реактивная мощность цепи равна алгебраической сумме реактивных мощностей всех ветвей:

	n
Q =	∑	Qk .
	1

причем реактивную мощность ветви с индуктивностью берут со знаком плюс, ветви с емкостью — со знаком минус. Для цепи рис. 2.16 реактивная мощность равна

Полная мощность цепи

Угол сдвига φ между общим током и напряжением определяют из векторной диаграммы или из выражения:

Графоаналитический метод не удобен для расчета разветвленных цепей: он отличается громоздкостью и невысокой степенью точности.

Для анализа и расчета разветвленных цепей переменного тока используют проводимости, с помощью которых разветвленную цепь можно преобразовать в простейшую цепь и аналитически   рассчитать   токи   и   напряжения   всех   ее   участков.

В цепях постоянного тока проводимостью называется величина, обратная сопротивлению участка цепи:

и ток в цепи выражается как произведение напряжения на проводимость:

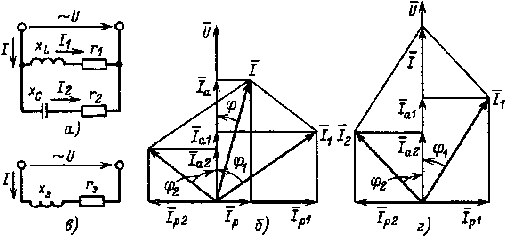Рис.   2.17.   Электрическая   цепь  (а),   ее   векторная   диаграмма   (б) и эквивалентная  схема (в);   векторная  диаграмма   цепи  при   резонансе

В цепях переменного тока существуют три проводимости — полная, активная и реактивная, причем только полная проводимость является величиной, обратной полному сопротивлению последовательного участка цепи.

Выражения проводимостей в цепях переменного тока можно получить следующим образом.

Ток в каждом неразветвленном участке цепи раскладывают на две составляющие, одна из которых есть проекция на вектор напряжения (активная составляющая тока Ia ), а другая - на линию, перпендикулярную вектору напряжения (реактивная составляющая тока Iр ).

Активная составляющая тока определяет активную мощность

реактивная составляющая тока - реактивную мощность

Из   векторной  диаграммы   цепи   рис.   2.17, а,   изображенной   на рис.   2.17, б,   следует,   что   активная   составляющая   тока I1 равна

I1a = I1 cos φ1  =	U	r	= Ur1/z12 = Ug1.
	z1	z1

Величина

называется активной проводимостью ветви. Реактивная составляющая тока I1 равна

Ilp = I1 sin φ1  =	U	xL	= UxL/z12 = Ub1.
	z1	z1

Величина

называется реактивной проводимостью ветви цепи с индуктивностью и в общем случае обозначается bL.

Аналогично определяют активную g2 и реактивную b2 проводимости второй ветви цепи:

Реактивная проводимость ветви с емкостью в общем случае обозначается bC.

Вектор тока первой ветви равен геометрической сумме векторов активной и реактивной составляющих тока

а значение тока

Выразив составляющие тока через напряжение и проводимости, получим

где у1 = 1/z1 = √g12 + bL12 — полная проводимость ветви.

Аналогично определяют и полную проводимость второй ветви:

Эквивалентные активную, реактивную и полную проводимости цепи получают следующим образом.

Вектор общего тока цепи равен геометрической сумме векторов токов Ī1 и Ī2:

и может быть выражен через активную и реактивную составляющие тока и эквивалентные проводимости всей цепи:

Активная составляющая общего тока (см. рис. 2.17, б) равна арифметической сумме активных составляющих токов ветвей:

а реактивная составляющая - арифметической разности реактивных составляющих этих токов:

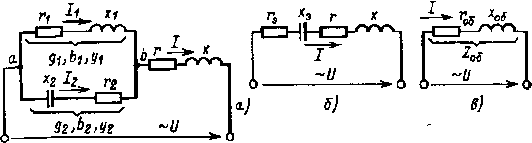Рис.   2.18.   К  расчету  разветвлен- ной   цепи  с   использова- нием   проводимостей

Из выражений (2.24) и (2.25) следует, что эквивалентная активная проводимость цепи равна арифметической сумме активных проводимостей параллельно включенных ветвей:

а эквивалентная реактивная проводимость — алгебраической сумме реактивных проводимостей параллельно включенных ветвей:

При этом проводимости ветвей с индуктивным характером нагрузки берут со знаком плюс, ветвей с емкостным характером нагрузки — со знаком минус. Полная эквивалентам проводимость цепи

По эквивалентным активной, реактивной и полной проводимостям можно определить параметры эквивалентной схемы (рис. 2.17, в) цепи.

Эквивалентные активное, реактивное и полное сопротивления цепи определяют с помощью выражений

Необходимо отметить, что если ΣbL > ΣbC, то эквивалентное сопротивление хэ будет индуктивным, если ΣbC > ΣbL —емкостным.

Смешанное соединение потребителей. Расчет цепи при смешанном соединении потребителей (рис. 2.18, а) может быть произведен путем замены ее простейшей эквивалентной цепью. Для этого вначале определяют активные, реактивные и полные проводимости параллельно включенных ветвей: g1, g2, b1, b2, у1, у2.

Затем находят эквивалентные активную, реактивную и полную проводимости параллельного участка цепи:

Далее определяют эквивалентные активное, реактивное и полное сопротивления параллельного участка цепи:

В результате расчетов цепь может быть заменена эквивалентной цепью (рис. 2.18, б), где все сопротивления включены последовательно. Общие  активное,  реактивное   и   полное   сопротивления   цепи   равны

Цепь приобретает простейший вид, изображенный на рис. 2.18, в. Общий ток цепи определяют по закону Ома:

Напряжение между точками а и b

Токи в параллельных ветвях равны