ЭЛЕКТРОТЕХНИКА

Глава   десятая
АСИНХРОННЫЕ  МАШИНЫ

10.2. ВРАЩАЮЩЕЕСЯ  МАГНИТНОЕ  ПОЛЕ

Допустим вначале, что все проводники одной фазы обмотки статора двухполюсного асинхронного двигателя размещены в двух диаметрально противоположных пазах и в обмотке действует постоянный ток.

Магнитное поле, созданное током одной фазы такой обмотки, будет иметь картину, изображенную на рис. 10.6. Магнитная цепь двигателя содержит ферромагнитные участки: сердечник статора и ротора и воздушный зазор между ротором и статором.

Для любой линии магнитной индукции по закону полного тока можно написать

где H0, Hст — напряженности магнитного поля соответственно в воздушном зазоре (l0) и в участках сердечников ротора и статора (lст); Iw — МДС одной фазы обмотки.

Следует отметить, что В и H в различных участках сердечника статора и ротора неодинаковые, например в зубцах между пазами статора, а также ротора они имеют наибольшее значение, поскольку сечение магнитопровода в зубцах наименьшее.

Так как H = B/μa , a μacт >> μ0, то H0 >> Hст и, следовательно,

Поэтому для упрощения анализа картины магнитного поля асинхронного двигателя можно полагать, что

2H0l0 ≈ ΣIw,

откуда и магнитная индукция в воздушном зазоре

Поскольку воздушный зазор одинаков по всей длине, из выражений (10.3), (10.4) вытекает, что напряженность и магнитная индукция   вдоль   всего   зазора   будут   иметь   соответственно

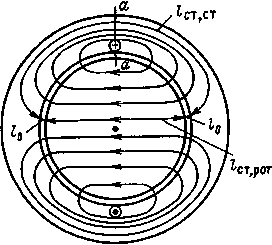Рис. 10.6 Картина магнитного поля, созданного током одной фазы обмотки двухполюсного асинхронного двигателя

одинаковые значения. На рис. 10.7, а изображен график распределения магнитной индукции в воздушном зазоре; для наглядности окружности сердечников статора и ротора развернуты в линию. Такой прямоугольный график распределения магнитной индукции непригоден: двигатель имел бы низкий КПД и неудовлетворительные характеристики. Наилучшие показатели двигатель имеет, когда магнитная индукция в воздушном зазоре распределяется по синусоидальному закону. Для получения графика, близкого к синусоиде, проводники одной фазы обмотки укладывают в возможно большее число пазов и выполняют обмотку с укороченным шагом. Если, например, одной фазой обмотки занято 10 пазов, то график магнитной индукции 1 будет иметь вид, изображенный на рис. 10.7, б. Этот график значительно ближе к синусоиде (изображена пунктирной линией). Получить идеальную синусоиду невозможно. Однако практически график распределения магнитной индукции в воздушном зазоре принимают за синусоиду.

---

1 Предполагается, что магнитная система не насыщена.

---

Проводники второй и третьей фаз обмотки создают аналогичные магнитные поля, но сдвинутые в пространстве на угол 120°. Если одну фазу обмотки подключить к сети однофазного тока, где напряжение изменяется во времени синусоидально, то магнитное поле будет изменяться во времени синусоидально с частотой тока сети. Таким образом, магнитное поле, созданное синусоидальным током одной фазы, распределяется вдоль воздушного зазора примерно синусоидально, неподвижно в пространстве и изменяется во времени.

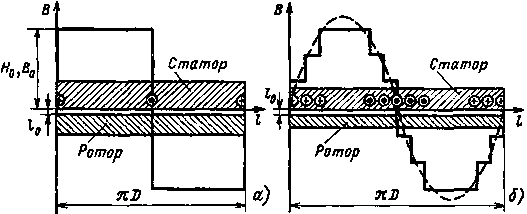Рис. 10.7. Графики распределения магнитной индукции в воздушном зазоре асинхронного двигателя: обмотка фазы заполняет два паза (а) и десять пазов (б)

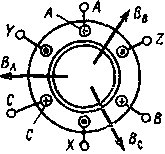Рис 10.8. Положительные направления токов фаз обмотки статора и соответствующие им положительные направления амплитуд магнитных индукций фаз обмотки статора двухполюсного асинхронного двигателя

Обмотка статора асинхронного двигателя соединяется звездой или треугольником и подключается к сети трехфазного тока. Поскольку каждая фаза обмотки имеет одинаковое число витков и они симметрично расположены по окружности статора, их сопротивление и амплитуда тока будут одинаковыми, но токи в фазах обмотки будут сдвинуты во времени относительно друг друга на 120°. Токи каждой фазы обмотки создадут магнитные поля, которые, очевидно, будут сдвинуты во времени на тот же угол. В результате сложения магнитных полей всех фаз образуется общее магнитное поле двигателя. Магнитная индукция результирующего магнитного поля оказывается распределенной вдоль воздушного зазора также по синусоиде, ее амплитуда не изменяется во времени и в 1,5 раза больше амплитуды магнитной индукции одной фазы. Результирующее магнитное поле вращается с постоянной частотой.

Для доказательства образования вращающегося магнитного поля воспользуемся графоаналитическим методом, с помощью которого построим картину магнитного поля для нескольких моментов времени периода переменного тока.

На рис. 10.8 изображены положительные направления токов в фазах обмотки статора и соответствующие им положительные направления амплитуд магнитных индукций двухполюсного асинхронного двигателя, а на рис. 10.9 — графики мгновенных значений токов в фазах обмотки статора.

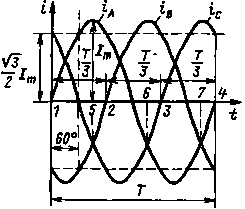Рис. 10.9. Графики мгновенных значений токов в фазах обмотки статора

В момент времени t = 0 (точка 1 на рис. 10.9) ток в фазе А равен нулю и она не создает магнитного поля. Магнитодвижущие  силы,  создаваемые  токами фаз В и С равны 1

iBw = iСw = Imw sin 60° =

=	√3	Imw =— Bm	√3	= BB = BC.
	2		2

---

1 Предполагается, что магнитная система не насыщена (В ~ Iw).

---

Ток фазы С положительный и, следовательно, направлен от начала к концу обмотки, ток фазы В отрицательный, и его действительное направление будет от конца к началу обмотки. На рис. 10.10, а изображена картина магнитного поля и векторная диаграмма для момента времени, соответствующего точке 1 рис. 10.9.

Амплитуда результирующего поля

На рис. 10.10, б и в изображены картины магнитных полей и векторные диаграммы для моментов времени, соответствующих точкам 2 и 3 (см. рис. 10.9) На рис. 10.10, г — е приведены графики распределения магнитных индукций вдоль воздушного зазора двигателя (πD — длина внутренней окружности сердечника статора), образованных током каждой фазы, и результирующего поля соответственно для моментов времени, отмеченных точками 5, 6, 7 (см. рис. 10.9). Пунктирными линиями обозначены магнитные индукции, соответствующие положительным направлениям тока при их амплитудных значениях, сплошными линиями — магнитные индукции, соответствующие действительным направлениям тока. Для момента времени, соответствующего точке 5 (см. рис. 10.9), ток фазы А положительный и равен амплитудному значению, токи фаз В и С отрицательные и равны половине амплитудного значения. Поэтому амплитуда магнитной индукции фазы А составит Вт и график поля совпадает с положительным направлением магнитных индукций, амплитуды магнитной индукции фаз В и С составят Вт/2, а их графики будут повернуты на 180° по отношению   к   положительным   направлениям.   Результирующее магнитное поле Вр можно получить путем сложения магнитных полей всех фаз 1.

---

1 Предполагается, что магнитная система не насыщена (В ~ Iw).

---

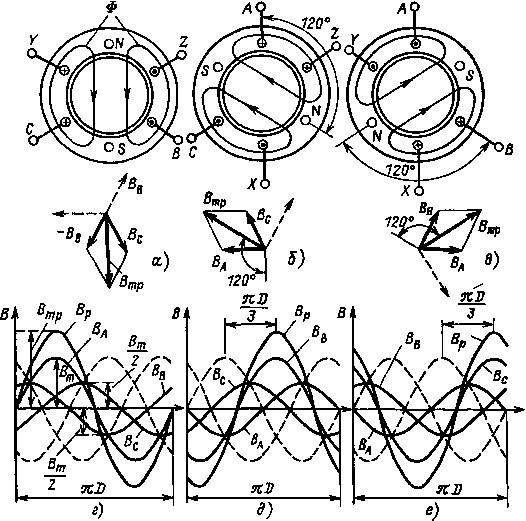Рис 10 10. К пояснению образования вращающегося магнитного поля двухполюсного асинхронного двигателя

Сравнивая картины магнитных полей и векторные диаграммы, легко убедиться в том, что за время Т/3 результирующее магнитное поле двухполюсного асинхронного двигателя повернется в пространстве на 120°, оставаясь неизменным по амплитуде. За время одного периода поле повернется на 360° (2π), т. е. сделает один оборот.

Угловая скорость поля

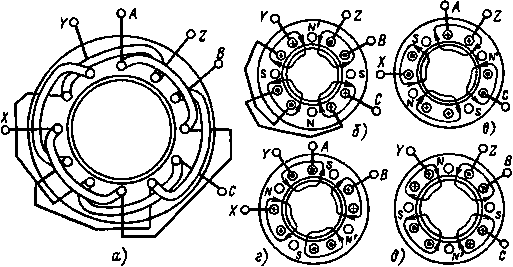Рис    10.11    Картина   магнитного  поля   четырехполюсного  асинхронного двигателя

Период, частота и угловая частота переменного тока связаны соотношением

Подставив в (10.6) вместо T его значение из (10.7), получим

Выразив ω0 через частоту вращения поля n0 в об/мин, а ω — через частоту f1

2πn0	= 2πf1,
60

получим

Из выражения (10.9) следует, что частота вращения магнитных полей всех двухполюсных асинхронных двигателей, включенных в промышленную сеть, составляет

n0 = 60 • 50 = 3000 об/мин.

Двигатели выполняются не только с двумя, но и с четырьмя, шестью, восьмью и т. д. полюсами; в общем случае они имеют р пар полюсов. Обмотка каждой фазы статора таких двигателей состоит из нескольких частей, которые соединяются между собой параллельно или последовательно.

На рис. 10.11, а показана обмотка асинхронного двигателя с четырьмя полюсами (р = 2). На рис. 10.11, б — д изображена картина результирующего магнитного поля двигателя соответственно для моментов времени, отмеченных точками 1, 2, 3 (см. рис. 10.9). Точками и крестиками обозначены направления тока для указанных моментов времени.

Из рис. 10.11 следует, что двигатель имеет четыре полюса и за время одного периода его поле повернется в пространстве па α0 = 180°, а в общем случае - на 360°/р. В начале периода полюс N' находился вверху, в конце периода он оказался внизу.

Угловая скорость поля

ω0 = 2π/Тр.

Подставив вместо Т его значение из (10.7)

и выразив ω0 через частоту вращения поля n0, а ω — через частоту f1, получим

2πn0	=	2πf1
60		р

откуда

Двигатели с р = 2 будут иметь n0 = 1500 об/мин, с р = 3 n0 = 1000 об/мин, с р = 4 n0 = 750 об/мин, с р = 5 n0 = 600 об/мин и т. д.

В паспортных данных обычно задается номинальная частота вращения двигателя nном . При решении задач и анализе работы двигателей, где необходимо знать n0, его выбирают как ближайшее большее из указанных при f1 = 50 Гц.

Например, nном = 1460 об/мин соответствует n0 = 1500 об/мин, nном = 960 об/мин — n0 = 1000 об/мин.

При расчетах некоторых сложных систем, например электрического вала и сельсинов, пользуются электрическими (α) и механическими (α0) углами: α0 — угол поворота поля статора за время t:

α — угол поворота вектора напряжения обмотки статора за тот же промежуток времени:

Подставив в (10.12) вместо t его значение из (10.13)

α0 = ω0α/ω,

а затем, выразив ω0 через со в соответствии с (10.10):

α0 =	ω		α	,
	p		ω

получим