Глава восьмая
ТРАНСФОРМАТОРЫ
8.4. РАБОТА ТРАНСФОРМАТОРА С НАГРУЗКОЙ
Для анализа работы трансформатора с нагрузкой уравнения электрического состояния первичной (8.4) и вторичной (8.5) цепей записывают в виде
U1 = - E1 + I1r1 + jI1x1,
| I1 = | U1 + E1 | . |
| r1 + jx1 |
U2 = E2 - I2r2 - jI2x2,
Как уже говорилось выше, при работе трансформатора с нагрузкой (см. рис. 8.1) во вторичной обмотке действует ток I2 и основной магнитный поток создают МДС обеих обмоток. Так как положительные направления действующих значений токов в первичной и вторичной обмотках одинаковые от начала к концу (см. рис. 8.1), то основной манитный поток обусловлен суммой МДС. Сумма МДС, она векторная, заменяется одной результирующей:
Iw1 + I2w2 = (Iw)рез .
При холостом ходе I2 = 0 и
(Iw)рез = I1w1 = I10w1
и создаваемый этой МДС магнитный поток Фm = Фm0. Значение ЭДС Е10, индуктируемой этим потоком, как следует из уравнения (8.6), почти равно U1, так как ток холостого хода I10 мал и падение напряжения от него в r1 и х1 пренебрежимо мало:U1 ≈ Е10.
При изменении нагрузки изменяются ЭДС Е1, магнитный поток и результирующая МДС трансформатора. Однако, как уже об этом говорилось, падение напряжения в первичной обмотке как при холостом ходе, так и при нагрузке невелико и практически можно допустить, что
Е1 = E10 = U1 и ЭДС не зависит от нагрузки.
Если это допустить, то необходимо предположить, что магнитный поток и создающая его МДС также не зависят от нагрузки и имеют те же значения, что и при холостом ходе:
Фm = Фm0 и (Iw)peз = I10w1.
Такое допущение намного упрощает анализ работы трансформатора и не вносит существенных погрешностей в расчетные формулы. Поэтому уравнение МДС (8.9) принято записывать в виде
I1w1 + I2w2 = I10w1,
Необходимо отметить, во-первых, что физические явления в трансформаторе довольно сложные и их нельзя объяснить, если допустить, что E1 и Фm не зависят от нагрузки.
Как, например, объяснить в этом случае, пользуясь уравнением (8.7 а), почему с изменением тока I2 изменяется ток I1? Невозможно. В действительности ток I1 изменяется потому, что изменяется ЭДС E1. Это вытекает из (8.7 а). В выражении (8.7 а) величины U1, r1, х1 не зависят от тока I2 и с его изменением остаются неизменными. Следовательно, I1 есть функция E1, а она вызвана магнитным потоком Фm(E = 4,44wfФm). Магнитный поток изменяется в результате действия МДС I2w2. Во-вторых, при нагрузках, значительно превышающих номинальные, например коротком замыкании, магнитный поток намного меньше, чем при номинальном режиме, и все сделанные выше допущения привели бы к недопустимым погрешностям в расчетных формулах. Разделив правую и левую части уравнения (8.10) на w1 и решив его относительно тока I1, получим
I1 = I10 - I2w2/w1 = I10 + I'2,
Из уравнения (8.11) вытекает, во-первых, то, что ток в первичной обмотке имеет две составляющие: ток холостого хода и ток, обусловленный нагрузкой, и, во-вторых, поскольку намагничивающий ток (ток холостого хода) не зависит от нагрузки, с изменением тока I2 в той же степени изменяется ток I1, что ранее было доказано с помощью закона сохранения энергии. Для качественного анализа и получения относительных количественных соотношений трансформатора с нагрузкой полезно использовать векторную диаграмму, которая является графическим отображением уравнений электрического состояния (8.7), (8.8) первичной и вторичной цепей трансформатора и уравнения токов (8.11).
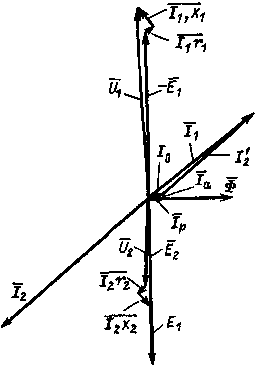 |
| Рис. 8.6. Векторная диаграмма нагруженного трансформатора |
На рис. 8.6 изображена векторная диаграмма при
Zн = rн + jxн . Необходимо отметить два важных положения, вытекающих из векторной диаграммы и рис. 8.1. Первое: напряжение вторичной обмотки почти совпадает по фазе с первичным (для идеализированного трансформатора совпадает точно). Второе: ток вторичной обмотки находится почти в противофазе с током первичной обмотки. Это означает, что МДС вторичной обмотки большую часть периода переменного тока является размагничивающей относительно МДС тока первичной обмотки (см. рис. 8.6).
Действительно, если напряжение u1 = U1msin ωt и направлено от начала к концу первичной обмотки, то, как это следует из векторной диаграммы, напряжение и2 можно записать так: u2 = U2msin (ωt - π) (угол несколько больше π, для идеализированного трансформатора точно π), но оно направлено от конца к началу вторичной обмотки. Если направление действия и2 принять таким же, как и1, — от начала к концу, то выражение и2 следует записать в таком виде: и2 = - U2msin (ωt - π) или u2 = U2msin ωt. Отсюда следует, что в первую часть периода начала обмоток имеют положительный потенциал относительно своих концов, а во вторую часть периода — отрицательный, а это означает, что u2 и u1 почти совпадают по фазе (для идеализированного трансформатора совпадают точно).
Ток в первичной обмотке имеет выражение i1 = I1msin (ωt - φ1) и направлен от начала к концу обмотки, ток во вторичной обмотке, как это следует из векторной диаграммы, равен
i2 = I2msin (ωt - φ1 - π) (угол несколько больше π, если же пренебречь током холостого хода I0, то точно π). Следовательно, когда ток (движение положительных зарядов) в первичной обмотке направлен от начала к концу, то во вторичной — от конца к началу и наоборот. Таким образом, мгновенное значение результирующей МДС трансформатора равно почти арифметической разности (см. рис. 8.12) МДС первичной и вторичной обмоток
i1w1 - i2w2 = i0w1,
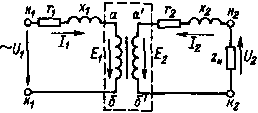 |
| Рис. 8.7. Схема трансформатора |
т. е. вторичный ток по отношению к первичному является размагничивающим, что соответствует правилу Ленца.
Определить значения величин, входящих в уравнения (8.7), (8.8), (8.11), например U2 и I2, при заданном значении нагрузки или построить график зависимости U2 от I2 возможно графически путем построений нескольких векторных диаграмм, что сопряжено со значительной затратой времени и погрешностью, связанной с неточностью графических построений. Поэтому для анализа и расчета трансформаторов используется схема замещения, в которой действительная магнитная связь между первичной и вторичной обмотками заменена гальванической, в результате чего возникает единая электрическая цепь переменного тока, позволяющая аналитически определить упомянутые выше величины. Схема замещения может быть получена следующим образом.
На рис. 8.7 изображена схема трансформатора, в которой активные сопротивления r1, r2 и индуктивные сопротивления x1 и х2 первичной и вторичной обмоток вынесены, магнитная связь осуществляется между идеализированными обмотками w1 и w2, в которых действуют ЭДС Е1 и Е2 от основного магнитного потока. Трансформатор, в котором r1, r2, x1, х2 равны нулю, называется идеализированным; он обведен на рис. 8.7 пунктирной линией. Для образования гальванической связи, казалось бы, необходимо соединить точки aа' и бб' (рис. 8.7). Однако делать этого нельзя, так как значения ЭДС Е1 и Е2 не одинаковы и в результате возникло бы короткое замыкание. Поэтому вначале надо уравнять потенциалы точек aа' и бб', т. е. ввести вместо действительного значения ЭДС Е2 его приведенное значение Е'2, вместо действительного тока I2 — его приведенное значение I'2. В результате реальный трансформатор заменяется трансформатором с одинаковым числом витков первичной и вторичной обмоток. Приведенное значение ЭДС
Е'2 = Е1 = Е2w1/w2 = Е2п.
Приведенное значение (абсолютное) тока I'2, как это вытекает из уравнения (8.11), равноI'2= I2w2/w1. Это же можно доказать исходя из того, что мощность (электромагнитная мощность), воспринимаемая вторичной обмоткой от первичной, в схеме замещения должна иметь то же значение, что и в реальном трансформаторе:
| E2I2 = E'2I'2 = Е2 | w1 | I'2, |
| w2 |
| откуда I'2 = I2 | w2 | . |
| w1 |
Поскольку в схеме замещения действуют приведенные значения Е'2 и I'2, отличные от действительных, необходимо привести и значения параметров вторичной цепи к первичной. В противном случае схема замещения не будет отражать реальные соотношения в трансформаторе.
Приведенные значения параметров вторичной цепи определяются из закона сохранения энергии: потери мощности в активном сопротивлении r'2 и реактивная мощность индуктивного сопротивления х'2 схемы замещения должны быть соответственно такими же, как в реальных r2 и х2 вторичной обмотки трансформатора. Приведенные значения определяются из соотношений
I22r2 = I22r'2; I22x2 = I22х'2; I22zн = I22z'н,
откудаr'2 = r2n2; х'2 = х2n2; z'н = zнn2.
Приведенное значение напряжения на вторичной обмотке трансформатора
U'2 = - U2w1/w2 = - U2n.
На рис. 8.8 изображена схема замещения трансформатора. Ветвь схемы замещения аб, в которой действует I10, называется намагничивающей, ее параметры r0 и х0 были рассмотрены при изучении холостого хода трансформатора. Схема замещения представляет собой разветвленную электрическую цепь переменного тока, что несколько усложняет расчеты, поэтому в практике обычно пользуются упрощенной схемой замещения. В упрощенной схеме замещения намагничивающую ветвь аб переносят к выводам первичной обмотки. Это вносит некоторые погрешности из-за падения напряжения в r1 и х1. Однако падение напряжения столь мало, что им можно пренебречь. Для большинства трансформаторов, как об этом уже говорилось, ток холостого хода I10 невелик и им можно пренебречь. Поэтому в упрощенной схеме замещения (рис. 8.9) предполагается, что I10 = 0 и I1 = I'2, и намагничивающая ветвь на схеме не указывается.
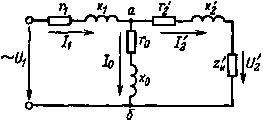 |
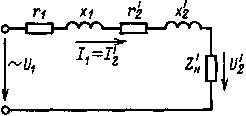 |
| Рис. 8.8. Схема замещения трансформатора | Рис. 8.9. Упрощенная схема замещения трансформатора |
Упрощенная схема замещения трансформатора может быть получена и другим путем, который и рассмотрим.
Выразив Е2 в (8.8) через E1(E2 = E1w2/w1 = E1/n) и решив уравнение относительно E1, получим
E1 = U2n + I2r2n + jI2x2n.
Подставив это значение Е1 в (8.7), получим
U1 = - U2n - I2r2n - jI2x2n + I1r1 + jI1x1.
Если пренебречь током холостого хода (I10 = 0), то из (8.11) следует, что
I1 = - I2w2/w1 = - I2/n.
Подставив это значение I1 в (8.12), получим
U1 = - U2n - I2r2n - jI2x2n - I2r1/n - jI2x1/n.
Выразив U2 и I2 в (8.13) через их приведенные значения U'2 = - U2n и I'2 = - I2/n, откуда
U2 = - U'2/n и I2 = - I'2п (знак минус появился вследствие того, что во вторичной обмотке ток I2 направлен от начала к концу, напряжение — от конца к началу, а в схеме замещения эти направления изменены на обратные), получим U1 = U'2 + I'2r2n2 + jI'2x2n2 + I'2r1 + jI'2x1.
Обозначив r2п2 = r'2 и х2п2 = х'2, получим
U1 = - U'2 + I'2r'2 + jI'2x'2 + I'2r1 + jI'2x1 = U'2 + I'2(r1 + r'2) +jI'2(x1 + x'2) =
=U'2 + I'2rк + jI'2xк = U'2 + I'2Zк.
Этому уравнению соответствует упрощенная схема замещения трансформатора, изображенная на рис. 8.9.
На основании закона Ома применительно к упрощенной схеме замещения можно записать
| I1 = I'2 = | U1 | . |
| √rк + r'н)2 + (xк + x'н)2 |
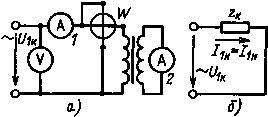 |
| Рис. 8.10. Схема опыта короткого замыкания (а), схема замещения трансформатора при коротком замыкании (б) |
Напряжение на выводах вторичной обмотки трансформатора
U'2 = U1 - I'2rк - jI'2xк .
Падение напряжения в обмотках трансформатора
ΔU = U1 - U'2 = I'2Zк,
где Zк = rк + jxк— полное сопротивление обмоток трансформатора.Сопротивления rк и xк определяются из опыта короткого замыкания, поэтому их называют параметрами короткого замыкания трансформатора.
Опыт короткого замыкания. Для выяснения соответствия значений расчетных данных сопротивлений rк и xк их действительным проводят опыт короткого замыкания. Опыт проводят и для определения rк и xк , когда их расчетные значения не известны.
Схема опыта короткого замыкания изображена на рис. 8.10, а. Значение полного сопротивления обмоток трансформатора zк составляет всего 5 — 15% сопротивления нагрузки, и если бы вторичная обмотка оказалась замкнутой накоротко при номинальном напряжении на первичной обмотке, то в обмотках трансформатора возник бы опасный для обмоток ток, больший номинального примерно в 10 — 20 раз.
Поэтому опыт проводят следующим образом. После сборки схемы опыта с помощью какого-либо регулятора напряжения устанавливают напряжение на первичной обмотке такого значения, при котором ток в обмотках равен их номинальным значениям. Напряжение при этом окажется не более 5 — 15% номинального. Это напряжение называют напряжением короткого замыкания и обозначают U1к . Затем записывают показание приборов. На рис. 8.10, б изображена схема замещения при опыте короткого замыкания.
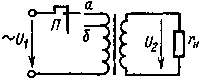 |
| Рис. 8 11. Схема трансформатора к примеру |
Мощность, измеряемая ваттметром, есть мощность всех потерь энергии в трансформаторе. Однако из-за малого значения напряжения на первичной обмотке и, следовательно, малого значения амплитуды магнитной индукции, что вытекает из выражения
U1к = E1к = 4,44 w1fBmSст , потери мощности в магнитопроводе, которые примерно пропорциональны квадрату амплитуды магнитной индукции, намного меньше, чем при номинальном напряжении, и значительно меньше потерь в обмотках трансформатора при номинальном токе и ими можно пренебречь. Таким образом, ваттметр фактически измеряет мощность потерь в обмотках трансформатора при номинальной нагрузке:
ΔРк = I21нr1 + I22нr2 = I21нr1 + I'22нr'2,
а так какI'2н = I1н и r'2 = r2n2,
тоΔPк = I1н2(r1 + r'2) = I1н2rк ,
откуда определяется значениеrк = ΔPк /I1н2.
Значение полного сопротивления определяется по показаниям вольтметра и амперметра и составляет
zк = U1к/I1к = U1к /I1н .
Значение идуктивного сопротивления определяется из выражения
xк = √zк2 - rк2.
В трансформаторах малой мощности (10 —500 Вт) rк > хк , средней rк < хк , большой rк << хк .
Пример 8.1. Как изменятся амплитуда магнитной индукции, ток холостого хода, напряжение на вторичной обмотке, токи во вторичной и первичной обмотках трансформатора, а также мощность, потребляемая трансформатором, и потери мощности в магнитопроводе трансформатора, если уменьшить число витков первичной обмотки на 5 — 10% (выключатель В переключить из положения а в положение б, рис 8.11)?
Решение. 1. Как вытекает из выражения
U1 ≈ E1 = 4,44fw1BmSст
при уменьшении числа витков первичной обмотки w1 увеличится амплитуда магнитной индукции Вm в магнитопроводе трансформатора, так как остальные величины, входящие в уравнение, не изменятся.2. Как вытекает из выражения
Bm = μaHm,
увеличится значение амплитуды напряженности магнитного поля в магнитопроводе.3. Из закона полного тока
Hст m lст + H0m l0 = I0mw1
следует, что с увеличением Нm увеличится и ток холостого хода I0m.4. Напряжение на вторичной обмотке U2 увеличится, что вытекает
из выражения
U2 = U1 w2/w1
5. Ток во вторичной обмотке I2 увеличится, что следует из закона Ома,
I2 = U2/zп
6. Ток в первичной обмотке I1 и мощность, потребляемая трансформатором Р, увеличится, что следует из закона сохранения энергии,
P = U2I2 = I22rп ≈ I1U1
или из уравненияĪ1=Ī0 + Ī'2.
7. Потери мощности в магнитопроводе трансформатора возрастут, поскольку они пропорциональны примерно квадрату амплитуды магнитной индукции, а она увеличилась
Пример 8.2. Как изменятся напряжение вторичной обмотки, ток холостого хода и потери мощности в магнитопроводе трансформатора, рассчитанного для работы в сети с частотой f = 50 Гц, если его включить в сеть с частотой f = 100 Гц того же значения первичного напряжения?
Решение 1 Как вытекает из выражения
U ≈ Е1= 4,44w1fBmSст ,
с увеличением частоты f уменьшится значение амплитуды магнитной индукции Bm , следовательно, и напряженности магнитного поля Hm(Bm = μаHm), и тока холостого ходаI0(Hст mlст + H0ml0= I0mw1).
2. Напряжение вторичной обмотки не изменится, так как оно определяется из соотношения
U2 = U1 w2 /w1.
3. Потери мощности в магнитопроводе трансформатора
| ΔPст = GΔP10Bmn( | f | )1,3 |
| 50 |
